八皇后问题(python)

问题描述

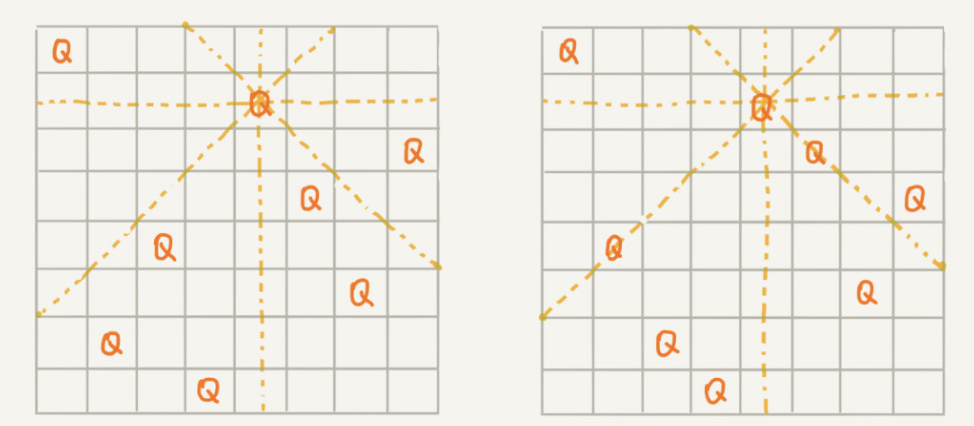
有一个 8x8 的棋盘,往里放 8 个棋子,每个棋子所在的行、列、对角线都不能有另一个棋子。如下,第一幅图是满足条件的一种方法,第二幅图是不满足条件的。
八皇后问题就是期望找到所有符合条件的情况.

将摆法抽象为数据结构

很显然,满足条件的摆法一定是每行有一个棋子. 我们可以定义一个列表,列表的索引代表行号(从 0 开始),值代表摆放的列位置(从 0 开始).

例如可以用列表[0,1,2,3,4,5,6,7]代表下面这种情况:

O * * * * * * *
* O * * * * * *
* * O * * * * *
* * * O * * * *
* * * * O * * *
* * * * * O * *
* * * * * * O *
* * * * * * * O

需要输出的时候我们只需要把该结构还原即可:

def print_queens(result):
    print('='*10)
    for i in result:
        print("* "*i,end="")
        if(i>=0):
            print("O ",end="")
        print("* "*(len(result) - i - 1))

如何判断一个棋子是否符合要求

我们的思路是,从上到下逐行摆放棋子,没摆放一个棋子后检查是否符合要求.

那么不符合的情况一共有三种:

1. 该棋子正上方已经有棋子存在;
2. 该棋子左上对角线已经有棋子存在;
3. 该棋子右上对角线已经有棋子存在;

O * * * * * * *
* * O * * * * *
* * * C * * * *
* * * * * * * *
* * * * * * * *
* * * * * * * *
* * * * * * * *
* * * * * * * *

以上情况可以用[0,2,-1,-1,-1,-1,-1,-1]表示,其中-1 表示还未进行该行的考察,我们要考察的行为第 2 行(从 0 开始).

我们将待考察行的索引记为 cur_index,待考察值为 value,三种情况分别可转换为列表的判断:

1. 该棋子正上方已经有棋子存在;
   • 该值在列表中已存在,例如[0,2,2,-1,-1,-1,-1,-1]
2. 该棋子左上对角线已经有棋子存在;
   • 索引先前推 n 位, 有 value - n = cur_index - n,例如[0,2,3,-1,-1,-1,-1,-1]
3. 该棋子右上对角线已经有棋子存在;
   • 索引先前推 n 位, 有 value - n = cur_index + n,例如[0,2,1,-1,-1,-1,-1,-1]

res = []

def check(row, column):
    # 逐行向上考察
    for (index, value) in enumerate(result[:row][::-1]):
        # 这三种分别表示在正上方,右上对角线,左上对角线存在棋子
        if value in [column, column + index + 1, column - index - 1]:
            return False
    result[row] = column
    return True

多层 for 循环嵌套考察所有情况

这种代码最好理解,但是写出来估计会疯掉,而且无法扩展为 n 皇后的问题.

def enum_queens_iter():
    length = len(result)
    for r0 in range(length):
        if check(0,r0):
            result[0] = r0
            for r1 in range(length):
                if check(1,r1):
                    result[1] = r1
                    for r2 in range(length):
                        if check(2,r2):
                            result[2] = r2
                            for r3 in range(length):
                                if check(3,r3):
                                    result[3] = r3
                                    for r4 in range(length):
                                        if check(4,r4):
                                            result[4] = r4
                                            for r5 in range(length):
                                                if check(5,r5):
                                                    result[5] = r5
                                                    for r6 in range(length):
                                                        if check(6,r6):
                                                            result[6] = r6
                                                            for r7 in range(length):
                                                                if check(7,r7):
                                                                    result[7] = r7
                                                                    print_queens(result)

转换为递归的形式

从上面的代码中我们可以看到有大量重复的代码,而且重复代码之间是有结构关系的.这种代码一般可以转换为递归的形式.

以下代码中,我们每次只考察待考察部分的第一行,符合要求再考察剩余部分.

result = [-1] * 8
def enum_queens(row_index):
    length = len(result)

    # 考察当前部分的第一行
    for i in range(length):
        if(check(row_index,i)):
            if row_index == length - 1:
                global total_num
                total_num+=1
                print_queens(result)
            # 考察剩余的部分
            enum_queens(row_index+1)

if __name__ == "__main__":
    enum_queens(0)