机器学习：正态方程 python实现

目录

• 前言
• 一、算法介绍
• 二、核心算法
  • 1. 公式
  • 2.python实现
• 总结

前言

使用python简单实现机器学习中正态方程算法。

一、算法介绍

与梯度下降算法相比，正态方程同样用于解决最小化代价函数J，不同的是，梯度下降算法通过迭代计算获得最小J的theta值，而正态方程则是通过直接对J进行求导，直接获得满足条件的theta值。

二、核心算法

1. 公式

正态方程通过矩阵运算求得theta。

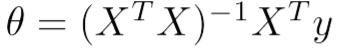
X为数据集中x的矩阵，y为数据集中y的矩阵。

2.python实现

import numpy as np

def NormalEquation(x,y):
    """
    正态方程：默认假设函数为：h = theta0+theta1x+theta2x
    x:x矩阵，第一列设置为x0 = 1
    y:y矩阵
    return:返回theta矩阵
    """ 
    theta = (x.T.dot(x)).I.dot(x.T).dot(y)
    return theta.astype(dtype = int)

def main():
    x = np.mat([[1,1],[1,2]])
    y = np.mat([[3],[5]])
    theta = NormalEquation(x,y)
    print(theta)

if __name__ == "__main__":
    main()

代码解释：

1. x.T是转置矩阵用法，.I是矩阵求逆
2. theta.astype(dtype = int)是为了让转置后的矩阵保持整型而已，无特殊要求可以直接返回theta。

总结

该篇文章简单介绍了通过python以及矩阵运算实现正态方程运算，从而使代价函数J的值最小。