11-02 NOIP练习赛
11-02 NOIP练习赛
为什么休息的天还要打练习赛,这不公平!!!!!!!!!! oh no!
但是三道题确实挺简单,也少见的很有意思。
[USACO23OPEN] Milk Sum S
题面翻译
给定数组 \(a_1,...,a_N\) 在数组中依次选出一个元素构成排列 \(b_1,...,b_N\) 。定义 $T = \sum _{i=1} ^N i \times b_i $ 。现在给出 \(Q\) 个操作,每个操作有两个数 \(x\) 和 \(y\) 表示将 \(a_x\) 替换成 \(y\) ,对于每一个操作求出操作后的 \(T\) 的最大值,每次操作后数组还原成原样。
输入格式
The first line contains \(N\).
The second line contains \(a_1\dots a_N\).
The third line contains \(Q\).
The next \(Q\) lines each contain two space-separated integers \(i\) and \(j\).
输出格式
Please print the value of \(T\) for each of the \(Q\) queries on separate lines.
样例输入 #1
5
1 10 4 2 6
3
2 1
2 8
4 5
样例输出 #1
55
81
98
\(1\le N\le 1.5\cdot 10^5\), \(0 \leq a_i \leq 10^8\),\(1\le Q\le 1.5\cdot 10^5\),\(0 \leq j \leq 10^8\).
第一题确实就比较简单,很明显排个序,更大的 \(a_i\) 理应适配给大的 \(i\) 以此来获得最大的 \(T\)。
替换操作又是没有后继性的,所以直接开搞。
朴素思想,将 \(a_i\) 改动以后,其实就是将其放到它该在的地方,在排好的序列中二分找到正确的地方,并把受影响的元素依次移动一个。
考虑对答案的贡献,首先预处理出原始的 \(T\),修改操作即先将 \(a_i\) 的贡献删掉,然后将改动后的新贡献加入,再考虑受影响的部分,预处理一个前缀和,受影响部分的贡献其实就是这段区间的综合。时间复杂度 \(O(nlogn)\)。
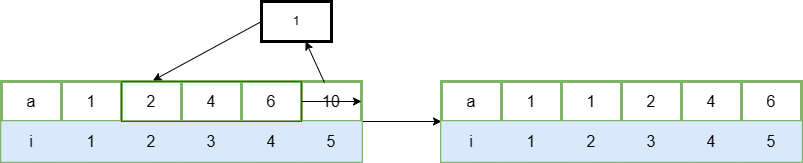
第一个样例解释
AC 代码:
#include<bits/stdc++.h>
using namespace std;
#define N 500005
#define int long long
long long a[N],f[N],pre[N],T=0;
long long n,q;
//我没有下一个运动会可以拿来错过了。
signed main(){
freopen("a.in","r",stdin);
freopen("a.out","w",stdout);
scanf("%lld",&n);
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
f[i]=a[i];
}
sort(f+1,f+1+n);
for(int i=1;i<=n;i++){
T+=f[i]*i;pre[i]=f[i]+pre[i-1];
}
scanf("%lld",&q);
while(q--){
long long x,y;
scanf("%lld%lld",&x,&y);
int i=upper_bound(f+1,f+n+1,a[x])-f-1;
int j=upper_bound(f+1,f+n+1,y)-f;
// printf("%d %d\n",i,j);
long long ans=T;
if(i>=j) ans=T-i*a[x]+j*y+pre[i-1]-pre[j-1];
else ans=T-i*a[x]+(j-1)*y+pre[i]-pre[j-1];
printf("%lld\n",ans);
}
return 0;
}
十年 OI 一场空,不开 long long 见祖宗
是的,赛时没开 long long 直接挂 18 分。
[USACO23OPEN] Field Day S
题目描述
Farmer John 的 \(N\) 个牛棚都会选出包含 \(C\) 只奶牛的队伍去参加户外聚会。所有奶牛的品种都只可能是根西牛(G)或荷斯坦奶牛(H)。
我们将两个奶牛队伍中,同一位置对应的两头奶牛品种不同的所有位置 \(i(1 \leq i \leq C)\) 的个数,定义为的两个奶牛队伍的差异。对于编号 \(1...N\) 的每个奶牛队伍 \(t\),请计算出 \(t\) 和其它所有队伍的差异的最大值。
输入格式
第一行包含两个整数 \(C\) 与 \(N\)。
接下来 \(N\) 行,每行有一个长度为 \(C\) 的,仅包含字母 G 和 H 的字符串,每行对应一支奶牛队伍。
输出格式
对于每个队伍,输出差异最大值。
\(2 \leq N \leq 10^5,1 \leq C \leq 18\)。
样例输入 #1
5 3
GHGGH
GHHHH
HGHHG
样例输出 #1
5
3
5
无法理解这道题 \(O(n^2)\) 只给我 5 分什么意思,感觉这道题太简单了吗?
这道题也是我感觉 3 道题之中最有意思的一道题。
本题可以使用广度优先搜索。
将 G 和 H 视为二进制下的 0 和 1,本题就可以转化成:
\(∀1≤i≤n\),求 \(\max popcount(a_i⨁a_j)\) 的值。
考虑广搜,对于每个给出的整数为源点开始搜。每次搜与它只差一位的数,若该数没被搜过,该数距离 +1,将该整数放入队列。
这样跑完以后,每个数对应的距离就是他们和他们相差位数最少的数差几位。注意是所有的数全部跑一边,处理出离他们最近的原点。
那么,我想要找到与 \(a_i\) 每位差的最远的数,就把 \(a_i\) 取反以后找和它每位差的最少的数,也就是我们刚刚跑出来的距离。
AC 代码:
#include<bits/stdc++.h>
using namespace std;
int main(){
freopen("b.in","r",stdin);
freopen("b.out","w",stdout);
ios::sync_with_stdio(false);
int c,n; cin>>c>>n;
vector<int> a(n),m(1<<c,-1);
queue<pair<int,int> > q;
for(auto &i:a){
for(int j=0;j<c;j++){
char x; cin>>x;
if(x=='G')i|=1<<j;
}
q.emplace(i,m[i]=0);
}
while(!q.empty()){
auto [u,w]=q.front(); q.pop();
for(int i=0;i<c;i++)
if(int v=u^(1<<i);m[v]==-1)
q.emplace(v,m[v]=w+1);
}
for(int i:a)cout<<c-m[(1<<c)-1^i]<<endl;
return 0;
}
[USACO23OPEN] Pareidolia S
题面翻译
Farmer John有的时候看东西会忽略一些字母,如把 bqessiyexbesszieb 看成 bessiebessie。定义 \(B(s)\) 表示把 \(s\) 中的若干个字母删去后,形成尽量多个 bessie 相连的形式 (bessiebessiebessieb...),返回 bessie 的最大数量。如 \(B(\text{"bqessiyexbesszieb"})=2\)。对字符串 \(s\) 计算 \(B(s)\) 是一个有趣的挑战,但FJ想到了一个更有趣的挑战:对 \(s\) 的所有子串进行计算B函数,并求和。\(s\) 的长度不超过 \(3\times 10^5\)。
样例输入 #1
bessiebessie
样例输出 #1
14
第三题题意还是比较简单 ,但是要 \(O(n)\) 做出来还是需要一些技巧。
这道题的关键是抓住每一个 bessie 对答案的贡献,而不能抓子串。
考虑类似动态规划的思路,对于每一个 \(i\),我们令 \(f_i\) 表示 以 \(i\) 作为结尾的区间中总共有多少 bessie 。然后从头到尾统计答案,对于每个 \(i\) 我们统计以 \(a_i\) 结尾的所有子串能有多少贡献,看代码,还是比较好理解,不行就拿样例理解理解。
AC 代码:
#include<bits/stdc++.h>
#define LL long long
using namespace std;
const LL N=5e5;
char c[N];
LL n,lst[N],f[N],ans;
int main(){
freopen("c.in","r",stdin);
freopen("c.out","w",stdout);
scanf("%s",c+1);
n=strlen(c+1);
for(int i=1;i<=n;i++){
if(c[i]=='b')lst[1]=i;
if(c[i]=='e')lst[2]=lst[1],lst[6]=lst[5];
if(c[i]=='s')lst[4]=lst[3],lst[3]=lst[2];
if(c[i]=='i')lst[5]=lst[4];
f[i]=f[lst[6]-1]+lst[6];
ans+=f[i];
}
printf("%lld",ans);
return 0;
}


