专题：最短路

最短路专题

由于最短路的内容有点多，所以从代码模板中提取出来单独做一个专题，后期有需要把字符串也单独整理一下。

在这里专门来注意一下 dijkstra 和 spfa 的区别，首先，dijkstra ** 不能处理负边权，不能处理负边权，不能处理负边权** 其次复杂度上肯定 DJ 更优，因为其每个节点只如队一次，其次 DJ 用优先队列，spfa 用队列。DJ 的 \(vis\) 数组是用来标记这个点是不是已经是最优点，是的话不进队，而 spfa 的 \(vis\) 数组是来标记该点是不是已经在队列里了，防止重复入队。

Dijkstra(迪杰斯特拉)

每次选取一个据起点最近的点，尝试更新与它相连的所有点。

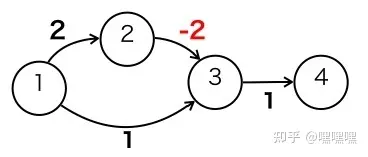
在补充一下 Dijkstra 不能求负权边的原因，因为其根本逻辑是确定当前点已经是离原点最近的点以后用该点更新其他点。

但是在有负权边时就无法保证当前更新出的点是离原点最近的，正确性无法得到保障（但是还是能保证较高的正确性）。

下面举一个范例

#include<bits/stdc++.h>
using namespace std;
#define N 200000
int vis[N],fir[N],nex[N],w[N],to[N],dis[N];
int tot=0;
int n,k,st;
typedef pair<int,int> PII;
priority_queue<PII, vector<PII>, greater<PII> >q;

void add(int x,int y,int z){
	nex[++tot]=fir[x];
	fir[x]=tot;
	to[tot]=y;
	w[tot]=z;
}

void dijkstra(){
	dis[st]=0;
	q.push(make_pair(0,st));
	while(!q.empty()){
		int u=q.top().second;
		q.pop();
		if(vis[u]==1) continue;
		vis[u]=1;
		for(int e=fir[u];e;e=nex[e]){
			int v=to[e];
			if(dis[v]>dis[u]+w[e]){
				dis[v]=dis[u]+w[e];
				q.push(make_pair(dis[v],v));
			}
		}
	}
}

int main(){
	scanf("%d%d%d",&n,&k,&st);
	for(int i=1;i<=k;i++){
		int x,y,z;
		scanf("%d%d%d",&x,&y,&z);
		add(x,y,z);
		add(y,x,z);
	}
	for(int i=1;i<=n;i++) dis[i]=99999999;
	dijkstra();
	printf("%d",dis[n]);
	return 0;
}

Floyd(佛洛依德)

选定一个点，尝试以该点为中转点，更新其他点

	for(int i=1;i<=m;i++){
		scanf("%d",&a[i]);
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			scanf("%d",&dis[i][j]);
		}
	}
	for(int k=1;k<=n;k++){
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				if(dis[i][k]+dis[k][j]<dis[i][j]){
					dis[i][j]=dis[i][k]+dis[k][j];
				}
			}
		}
	}

SPFA(Bellman-Ford队列优化)

SPFA 不可能死的，只要 Bellman-Ford 还在，SPFA 永存！！！！！！！

跟 Dijkstra 思路不同，但略有相似，SPFA 是只要把我能优化的点都放进队列，依次来松弛（优化），直到我松弛不动了，所以一个点允许多次进栈，复杂度肯定没有 Dijkstra 优，但是可以处理负权边和判断负环。

先放起点，然后只要该点被松弛了，就松弛与该点相连的所有的点。

#include<bits/stdc++.h>
using namespace std;

int first[100005],dist[100005];
int nex[200100],to[200100],w[200100];  
int n,m,tot=0;
bool vis[100005];        //vis[i]=true表示点i已经在队列中

void add(int x,int y,int z){
	nex[++tot]=first[x];
	first[x]=tot;
	to[tot]=y;
	w[tot]=z;
}

void spfa(){
    dist[1]=0;
    queue<int>q;
    q.push(1);
    vis[1]=true;
    while(!q.empty()){
        int u=q.front();
        q.pop();
        vis[u]=false;
        for(int e=first[u];e;e=nex[e]){
            int v=to[e];
            if(dist[u]+w[e]<dist[v]){
                dist[v]=dist[u]+w[e];
                if(!vis[v]){  
                    q.push(v);
                    vis[v]=true;
                }
            }
        }
    }
}

int main(){
	memset(dist,0x3f,sizeof(dist));
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		int x,y,z;
		scanf("%d%d%d",&x,&y,&z);
		add(x,y,z);
	}
	spfa(); 
    if(dist[n]==0x3f3f3f3f) printf("impossible\n");
    else printf("%d\n",dist[n]); 
	return 0;
}