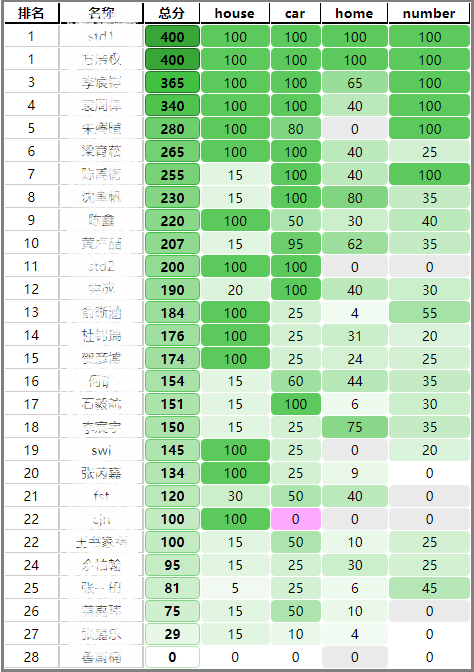
SXYZ-7.3训练赛
T1
房
啥啥啥，T1又又又爆了，整个人精神状态 良好。
解题思路
考虑数据保证任意两个房子不重合
建一个结构体存两边
最后判断一下
\(>t\) 加两个
\(==t\) 加一个
== 但是！！！！，没有排序！！喜提5分 ==
/*
刚刚写思路咋卡退了？？
考虑数据保证任意两个房子不重合
建一个结构体存两边
最后判断一下
>t加两个
==t加一个
*/
#include<bits/stdc++.h>
using namespace std;
#define N 300000
int x[N],a[N],n,t;
struct nod{
double l,r;
}f[N];
bool cmp(nod a,nod b){
return a.l<b.l;
}
int main(){
freopen("house.in","r",stdin);
freopen("house.out","w",stdout);
scanf("%d%d",&n,&t);
for(int i=1;i<=n;i++){
scanf("%d%d",&x[i],&a[i]);
}
for(int i=1;i<=n;i++){
f[i].l=x[i]-(a[i]/2.0);
f[i].r=x[i]+a[i]/2.0;
}
sort(f+1,f+1+n,cmp);
int ans=2;
for(int i=1;i<n;i++){
if((f[i+1].l-f[i].r)>t) ans+=2;
if((f[i+1].l-f[i].r)==t) ans++;
}
printf("%d",ans);
return 0;
}
T2
车
考虑暴力时间复杂度 \(O(n^2k)\) ,
由于是环，于是破环为链。
从头到尾扫一遍。、
6 4
2 2 1 3 3 1
3 2 4 11
很遗憾没有想出 \(O(nk)\) 的正解，因为我状态转移不了。
写了个模拟退火，感觉跑的还挺快
喜提25分
又细想了一下双指针做法，但是感觉实现起来很困难。
T4
数
看到题目暴力就有了，写一个 get 函数，然后从1枚举到 R，看是否符合条件。
ULL get(ULL m){
ULL sum=0;
while(m!=0){
sum+=m%10;
m=m/10;
}
return sum;
}
比赛时捞了45分。
然后尝试打表暴力优化，然而好像极限是55分，\(1e18\) 过于强悍。
for(int i=0;i<=1e6;i++){
if(i%10==0)
biao[i]=get(i);
else biao[i]=biao[i-1]+1;
}
for(int i=1;i<=R;i++){
if(i*k<=1e6){
if(biao[i]==biao[i*k]) ans++;
}
else{
if((biao[i/1000000]+biao[i%1000000])==(biao[i*k/1000000]+biao[(i*k)%1000000])) ans++;
}
}
思考正解数位 DP，
设 \(dp[i][0/1][j][p][t]\) 表示填到了第 i 位，卡不卡上界，\(f(x)=j\) ，\(f(k×x)=p\) （不计算最高位），需要向最高位进 t 的 x 有多少个。
所以这个 0/1 就表示后面的 i 为和 R 后 i 位的大小关系，如果填的数大于 R 后 i 为，那么这个状态就是1；否则就是0
至于转移，就比较简单，我们枚举这一位上填什么数y，那么对于x，数位和增加了y，对于 \(k×x\)，这一位上直接来一个乘法是 \(k×y\)，还有之前的进位 t，于是就是 \((k×y+t)%10\)，新的进位就是 \((k×y+t)/10\)。
最后的答案就是 \(∑idp[lgR][0][i][i][0]\)，我们把 \(j−p\) 看成一维状态就好了
AC代码：
#include<bits/stdc++.h>
#define re register
#define LL long long
LL dp[25][2][1000][500];
int m,w,a[25],M=250;LL n;
inline void split(LL x) {
while(x) a[++w]=(x%10),x/=10;
}
int main() {
freopen("number.in","r",stdin);
freopen("number.out","w",stdout);
scanf("%lld%d",&n,&m);
dp[0][0][0][M]=1;
split(n);
for(re int i=0;i<w+3;i++)
for(re int j=0;j<2;++j)
for(re int k=0;k<1000;++k)
for(re int p=M-2*i*9;p<=M+2*i*9;++p) {
if(!dp[i][j][k][p]) continue;
for(re int t=0;t<10;++t)
dp[i+1][t==a[i+1]?j:t>a[i+1]][(k+t*m)/10][p+t-(k+t*m)%10]+=dp[i][j][k][p];
}
printf("%lld\n",dp[w+3][0][0][M]-1);
return 0;
}
