SXYZ-6.28训练赛

今天上午出中考成绩，所以下午打了一场训练赛，只有两个小时，没有昨天毒瘤，但也很毒瘤（还是模拟赛好）

关于中考可以看我的中考游记

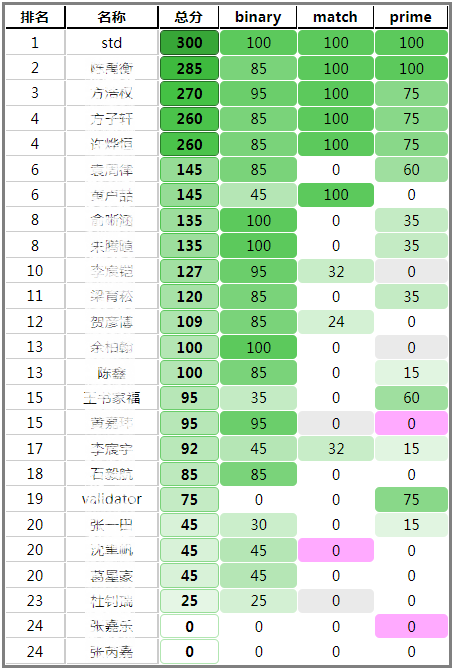
（为了保护隐私，以后都把姓名涂掉）

为什么还是倒数啊~

T1 binary

二分哥
这么简单的T1不明白为什么没有切，当时肯定脑袋抽抽l，奇偶性都没有看出来。

首先我们考虑怎么快速还原这个序列。
很显然的一个贪心策略就是假设序列为 \(a[i]\) ，不断把 \(a_{a_i}\) 与 \(a_i\) 交换直到\(a_i=i\)。
这样做我们发现交换次数是 \(O(n)\) 级别的。
然后我们发现要一个序列交换后形成交换前的序列交换次数只能是偶数。所以该交换次数与Petr或Alex的奇偶性相同。
于是只要判一下奇偶即可。

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1000005;
int aa[maxn];
int main(){
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i)
        scanf("%d", &aa[i]);
    int ans = 0;
    for(int i = 1; i <= n; ++i){
        while(aa[i] != i){
            swap(aa[aa[i]], aa[i]);
            ans++;
        }
    }
    if((n & 1) == (ans & 1)) // 判断奇偶性相同
        puts("Petr");
    else
        puts("Um_nik");
    return 0;
}

T2 match

啥，最大匹配是啥？不知道，溜了，溜了

T3 prime

质数
很有趣的一道数学思维题，暴力15分，打表素数，双指针移动算合，看是否符合目标。（很科学啊）

正解竟然用了 Miller-Rabin 来判断素数，好高级，后面研究一下再回来补一下。