SXYZ-6.27专题比赛
好的,现在正式定义今天的比赛为一场伤心的比赛。
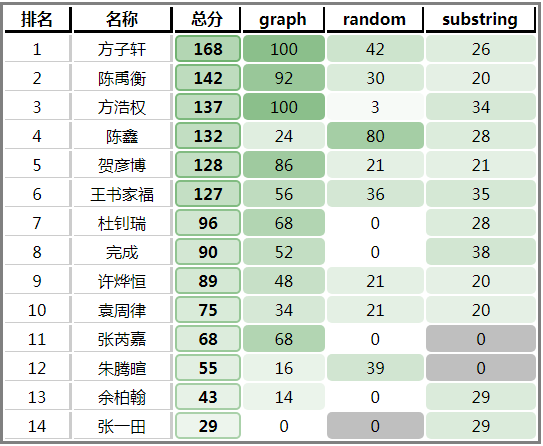
↑这张图片首先能说明一些问题,但这并不是关键。
↓这才是伤心的关键
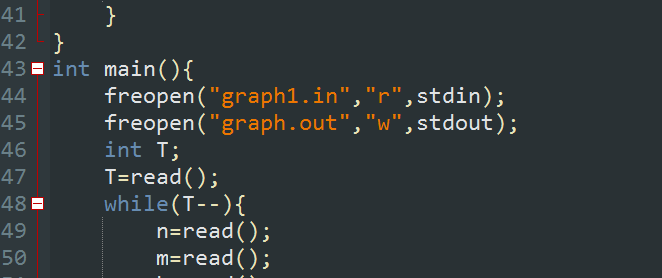
↑第一题文件输入输入爆
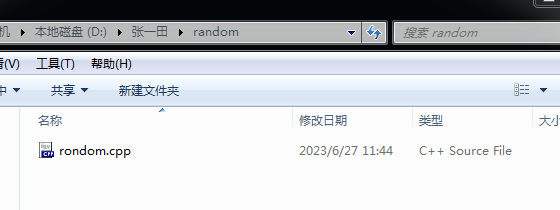
↑第二题文件名直接爆
评语,一个比一个离谱!
然后只是很简单的把这两个小错误改正确以后就有83分了,不知道该喜还是该悲。
上图
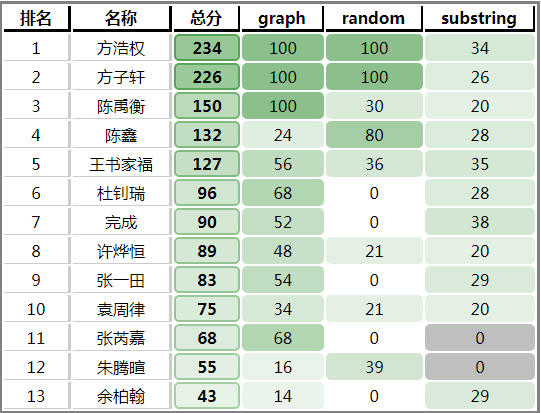
Ps:这是第一次犯这种SB错误,主要是平时自己就很小心。但依旧:
吃一堑,长一智
好的,就在刚刚,一脸雾水听完题目分析出来,又发现一个惊人事实,那就是我T2的文件输入输出名都是错的!!!!
(狂喜)
T1 graph
图
首先考虑暴力做法+优化,拿了54分,思路是遍历每一个点,一每一个点为起点, dfs 深搜 K 个节点,跟 ans 取个最大值,最优解一定在这其中。
54分代码:
#include<bits/stdc++.h>
using namespace std;//听我说谢谢你,因为有你。。。。
#define N 20000
int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=x*10+ch-'0';
ch=getchar();
}
return x*f;
}
int nex[N],first[N],w[N],to[N],tot=0,vis[N];
int n,m,k,ans;
void add(int x,int y,int z){
nex[++tot]=first[x];
first[x]=tot;
to[tot]=y;
w[tot]=z;
}
void dfs(int u,int fa,int st,int sum){
if(st==k){
ans=max(ans,sum);
return ;
}
++st;
for(int e=first[u];e;e=nex[e]){
int v=to[e];
if(v!=fa&&vis[v]==0){
vis[v]=1;
sum+=w[e];
// printf("u%d,v%d,w%d,st%d,sum%d\n",u,v,w[e],st,sum);
dfs(v,u,st,sum);
vis[v]=0;
sum-=w[e];
}
}
}
int main(){
freopen("graph.in","r",stdin);
freopen("graph.out","w",stdout);
int T;
T=read();
while(T--){
n=read();
m=read();
k=read();
tot=0;
ans=0;
memset(first,0,sizeof(first));
memset(vis,0,sizeof(vis));
for(int i=1;i<=m;i++){
int a,b,c;
a=read();b=read();c=read();
add(a,b,c);
add(b,a,c);
}
for(int i=1;i<=n;i++){
dfs(i,0,1,0);
}
if(ans!=0) printf("%d\n",ans);
else printf("-1\n");
}
return 0;
}
思考正解做法,
color coding 对图中的点随机染色,色彩个数为 k,然后进行 dp,设 \(f[i][S]\) 为当前 i 点颜色合集为 S 的权值。
令所有 \(f[i][S] = −inf\),然后对于每个顶点 x 和其颜色 col[x],f[1 << col[x]][x] = 0。然后从小到大枚举状态 S,
每一个状态 S 下枚举边,对于每条边我们记其相邻 2 端为 xx, yy,边权为 zz。
重复执行足够多次以后取最优解。
#include<bits/stdc++.h>
const int N=1e4+5,B=500;
using namespace std;
mt19937 rnd(19260817);
int n,m,k,col[N],S;
struct edge{int x,y,z;}e[N];
int f[N][64];
int check()
{
for(int i=1;i<=n;i++)
{
for(int j=0;j<S;j++)f[i][j]=-2e9;
f[i][1<<col[i]]=0;
}
for(int j=0;j<S;j++)
for(int i=1,xx,yy,zz;i<=m;i++)
{
xx=e[i].x;yy=e[i].y;zz=e[i].z;
if((j>>col[xx])&1)f[xx][j]=max(f[xx][j],f[yy][j^(1<<col[xx])]+zz);
if((j>>col[yy])&1)f[yy][j]=max(f[yy][j],f[xx][j^(1<<col[yy])]+zz);
}
int res=-1;
for(int i=1;i<=n;i++)res=max(res,f[i][S-1]);
return res;
}
int ans;
int T;
int main()
{
freopen("graph.in","r",stdin);
freopen("graph.out","w",stdout);
ios::sync_with_stdio(false);cin.tie(0);
cin>>T;
while(T--){
cin>>n>>m>>k;S=1<<k;
for(int i=1;i<=m;i++)cin>>e[i].x>>e[i].y>>e[i].z;
ans=-1;
for(int i=1;i<=B;i++){
for(int j=1;j<=n;j++)col[j]=rnd()%k;
ans=max(ans,check());
}
cout<<ans<<'\n';
}
return 0;
}
T2 random
随机
这道题考场没写出暴力,啥,暴力都没写出来,主要是图的数据结构只会邻接表,不会以边存图。
来看一看全场做高分80分陈鑫的做法:模拟退货,而且思想异常的朴素,这就是高手与我的区别吗,随机将点排个序,然后遍历一遍,求前第 i 个做删点处理的代价,多做几次求 min。
80分大佬代码:
#include <bits/stdc++.h>
#define eb emplace_back
using namespace std;
using ll = long long;
mt19937 mt(random_device{}());
int t, n, m;
ll a, b;
ll ans;
pair <int, int> ed[45];
vector <int> gra[45];
bool mp[45][45];
bool vis[45];
int bs[45];
ll js() {
ll ans = a * m;
for (int j = 0; j <= n; ++j) {
memset(vis, 0, sizeof(vis));
int totp = j;
for (int i = 1; i <= j; ++i) {
bool flag = 0;
for (auto &k : gra[bs[i]]) {
if (!vis[k]) flag = 1;
vis[k] = 1;
}
if (!flag) --totp;
}
int tot = 0;
for (int k = 0; k < m; ++k) if (vis[k]) ++tot;
ans = min(ans, b * totp + a * (m - tot));
}
return ans;
}
void mnth() {
double T = 100000, dt = 0.99;
while (T > 1e-8) {
int x = mt() % (n - 1) + 1, y = mt() % (n - x) + x + 1;
swap(bs[x], bs[y]);
ll tmp = js();
if (tmp < ans) {
ans = tmp;
} else if (exp(- abs(ans - tmp) / T) * 6553600 < mt() % 6553600) {
swap(bs[x], bs[y]);
}
T *= dt;
}
}
int main() {
freopen("random.in", "r", stdin);
freopen("random.out", "w", stdout);
scanf("%d", &t);
while (t--) {
scanf("%d%d%lld%lld", &n, &m, &a, &b);
for (int i = 1; i <= n; ++i) gra[i].clear();
memset(mp, 0, sizeof(mp));
memset(bs, 0, sizeof(bs));
ans = 1e18;
for (int i = 0; i < m; ++i) {
scanf ("%d%d", &ed[i].first, &ed[i].second);
gra[ed[i].first].eb(i);
gra[ed[i].second].eb(i);
}
for (int i = 1; i <= n; ++i) bs[i] = i;
srand(time(NULL));
random_shuffle(bs + 1, bs + n + 1);
mnth();mnth();mnth();
mnth();mnth();mnth();
mnth();mnth();mnth();
printf("%lld\n", ans);
}
return 0;
}
T3 substring
子串Ⅰ
考场上做了个简单判断,按照二的幂次分别输出0和1,然后随机情况输出0和1,竟然骗 了29.没想到这道题正解竟然是根据特殊性质做的,叫个什么 De Bruijn 序列。跑了,跑了。
不过部分分是可以拿de:
M.A.Martin 于 1934 年证明了以下贪心算法对所有的 n ≥ 2 都可以构造出一个长度
2n 的 De Bruijn 序列:
-
写出 n 个 0。
-
如果在序列尾部添加一个 1 后,和前面相连构成已经出现过的长为 n 的 01 子串,
则在序列尾部添加一个 0,否则在序列尾部添加一个 1。
- 序列若还不够 2n 项,则返回步骤 2。否则序列就是一个长度为 2n 次的 De Bruijn
序列。


