SXYZ-6.26模拟赛
没有爆零,足矣。
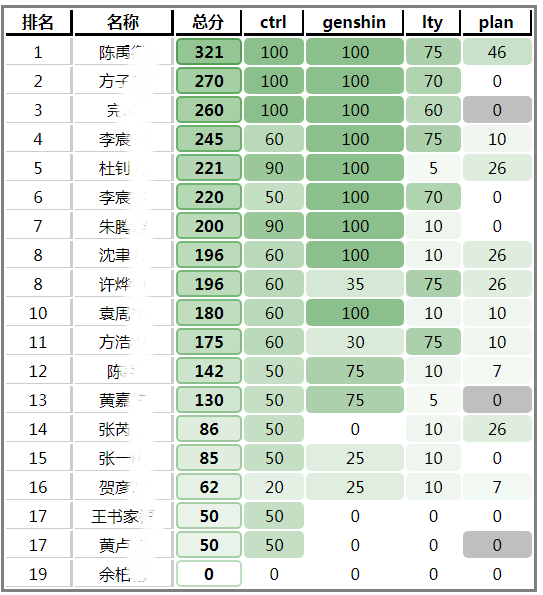
发现绍兴一中机房的一个特点:键盘打得贼响!!
T1 ctrl
啃臭键在哪里
(中文名我都不好意思大打)
第一遍测T1一分都没得啊!
这跟题目描述自相矛盾有关,导致我只是轻微考虑了一下 \(a[i]\) 为负的情况。
但是没有考虑的是 \(p[i]\) 竟然也可以为零
仁者见仁,智者见智吧
一天以后的现在晚上8:00,终于把一二问的正解打出来了。主要是昨天没法测,今天lemon又频频炸掉。还好在super OJ上AK了,回来把题解补上。
T1看了题解后打对了,解题思路很巧妙,与我之前分别算法不同。正解是相对于一种状态(冰之格),把翻:转每一个各自的贡献都放在一个新数组中,情况一共分为四类:
- 翻同种状态(翻冰之格)
- $a[i]\geq0 $ 不选,反转后贡献 \(-p[i]\)
- \(a[i]\leq0\) 初始选,反转后无法选择,贡献为 \(a[i]-p[i]\)
- 翻不同状态(翻火之格)
- \(a[i]\geq0\) 翻转后依然不选(重点,当时没搞懂),贡献为 \(-p[i]\)
- \(a[i]\leq0\) 翻转后选,贡献 \(a[i]-p[i]\)
对于当前情况的贡献数组sort一下,去前m个整数即可,是不是很妙!!
这是AC代码:
#include<bits/stdc++.h>
using namespace std;
#define N 800000
int n,m,p[N],a[N],b[N],fa[N],fb[N];
long long suma=0,sumb=0;
int main(){
freopen("ctrl.in","r",stdin);
freopen("ctrl.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=n;i++) scanf("%d",&p[i]);
for(int i=1;i<=n;i++){
scanf("%d",&b[i]);
if(b[i]==1&&a[i]>=0) suma+=a[i];
if(b[i]==0&&a[i]>=0) sumb+=a[i];
}
for(int i=1;i<=n;i++){
if(b[i]==1){
if(a[i]<0) fa[i]=-p[i];
else fa[i]=-a[i]-p[i];
}
else{
if(a[i]<0) fa[i]=-p[i];
else fa[i]=a[i]-p[i];
}
if(b[i]==0){
if(a[i]<0) fb[i]=-p[i];
else fb[i]=-a[i]-p[i];
}
else{
if(a[i]<0) fb[i]=-p[i];
else fb[i]=a[i]-p[i];
}
}
sort(fa+1,fa+1+n);
sort(fb+1,fb+1+n);
int ma=m,mb=m;
for(int i=n;i>=1;i--){
if(fa[i]>0&&ma>0) suma+=fa[i],ma--;
if(fb[i]>0&&mb>0) sumb+=fb[i],mb--;
}
printf("%lld",max(suma,sumb));
return 0;
}
T2 genshin
原神,启动!
这道题刚刚才调对,思路就是疯狂分类讨论,我的答题思路没错,但因为if过多,加上多重样例,被卡掉了。
简单说一下思路,以黑白相邻的填充方法填充整个区间,发现角落里的贡献是2,边上贡献是3,其余贡献是4。发现用这些数可以任意组成 \(1\)~\(2*n*(n-1)\) 中除了 \(1\) ,和 \(2*n*(n-1)-1\) 外,其他均可用2,3,4组和而成。中间还要注意,我是以4位基数,而四的个数只足够完全覆盖一般,也就是 \(n*n(n-1)\),可以发现剩下一般与前一半是对称的。所以这道题就做出来了。判断输出方法可能有待改进。
以下是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n4,n2,n3,sum,n,m,mm;
int check(){
int m4=0,m2=0,m3=0;
mm=m;
int f=0;
if(m>n*(n-1)){
mm=(2*n*(n-1)-m);
f=1;
}
if(mm%2==1){
m3=1;
mm-=3;
}
m4=min(n4,mm/4);
m2=(mm-m4*4)/2;
// cout<<" "<<m3<<" "<<n3;
if(f){
n4-=m4;n3-=m3;n2-=m2;
}
else{
n4=m4;n3=m3;n2=m2;
}
return 1;
}
int main(){
freopen("genshin.in","r",stdin);
freopen("genshin.out","w",stdout);
int T;
scanf("%d",&T);
while(T--){
scanf("%d%d",&n,&m);
if(n==1||m==1||m>2*n*(n-1)||m==2*n*(n-1)-1){
printf("Impossible\n");
continue;
}
if(m<=n){
printf("Possible\n");
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(i==1&&j<=m-1) printf("1");
else printf("0");
}
printf("\n");
}
continue;
}
int halfn=(n*n+1)/2;
if(n%2==0){
n2=2;n3=(n/2-1)*4;n4=halfn-n3-n2;
}
else {
n2=4;n3=((n+1)/2-2)*4;n4=halfn-n2-n3;
}
// printf("n:%d,n2:%d,n3:%d,n4:%d\n",n,n2,n3,n4);
if(check()){
printf("Possible\n");
int flag=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
flag=flag^1;
if(i==1&&j==1&&n2>0){ printf("1"),--n2;continue;}
if(i==1&&j==n&&n2>1){ printf("1"),--n2;continue;}
if(i==n&&j==1&&n2>1){ printf("1"),--n2;continue;}
if(i==n&&j==n&&n2>0){ printf("1"),--n2;continue;}
if(flag==1&&i==1&&j!=1&&j!=n&&n3>0){ printf("1"),--n3;continue;}
if(flag==1&&j==1&&i!=1&&i!=n&&n3>0){ printf("1"),--n3;continue;}
if(flag==1&&i==n&&j!=1&&j!=n&&n3>0){ printf("1"),--n3;continue;}
if(flag==1&&j==n&&i!=1&&i!=n&&n3>0){ printf("1"),--n3;continue;}
if(flag==1&&i!=1&&j!=1&&i!=n&&j!=n&&n4>0){ printf("1"),--n4;continue;}
printf("0");
}
printf("\n");
if(n%2==0) flag=flag^1;
}
}
}
return 0;
}
备:这道题改出来确实不容易,完全坚定自己思路肝出来的一道题,祭。
T3 Ity
雨田天宇
这道题解决方法偏数学数论,代码没有打出来。但是有思路。
考场暴力有十分,非常朴素,暴力枚举每一种a,排完序后求贡献,时间复杂度 \(O(!n*nlogn*n)\) 很明显,这个暴力过于朴素。
对绝对值进行转化 \(\sum^n_{i=1}\sum^m_{j=1}(a_i \leq j)\oplus(a_{n-i+1} \leq j)\)
交换一下 \(\sum^m_{j=1}\sum^n_{i=1}(a_i \leq j)\oplus(a_{n-i+1} \leq j)\)
枚举 i ,枚举 j,计算贡献。
T4 Plan
不会,当时题都没看,溜了,溜了~


