整理一些学过的数据结构和算法

匆匆忙忙中学了很多算法，但基本都是打个板子就跑路了，有些算法有个人比较深入和独特的见解，但大部分，只是实现例题的需求，对算法的作用似懂非懂，所以写篇博客整理一下。

---

无旋平衡树（treap）

---

高级数据结构：树和堆

可以允许的操作：插入，删除，查询某数排名，查询某排名的树（第K大），求某数的前驱，后驱（X的前一个数或后一个）

特点：使用随机数pri对每一个数划分优先级，实现堆。键值key对每一个数排序，实现树，满足每一个结点的左儿子比他小，右儿子比他大。

核心：分裂与合并（split&merge）

---

分块

---

区间信息维护与查询

可以允许的操作：单点更新，区间更新，区间查询

特点：O根号类暴力算法，简单快捷，效率较差

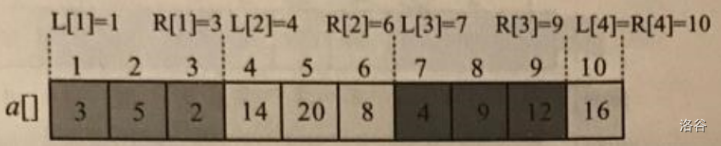
核心：打懒标记add[ ],和区块和sum[ ]

---

可持久化线段树

---

可以允许的操作：查询区间内第K小的数

---

补充：

前置：权值线段树

节点范围是一个区间，节点储存该值域内的元素个数，如图

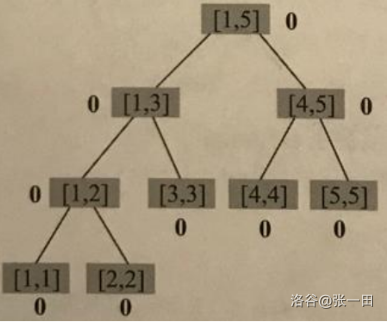
如此，每加入一个数，就会产生一个新的权值线段树，但都分开存储，占用的空间太大了，于是：

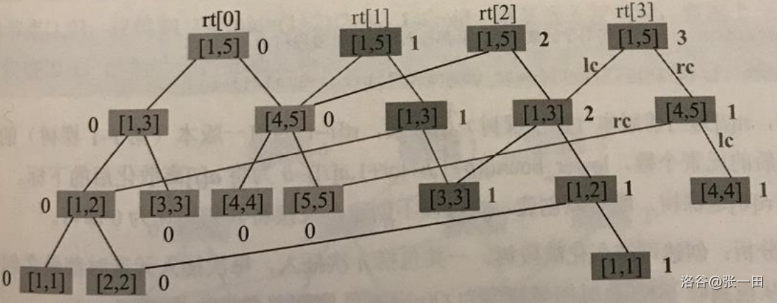
可持久化线段树来喽！

每插入一个节点，新建一个根节点，将改变了的节点重建，其他重复节点沿用。

实例：依次插入{3,1,4,2,3,5,3,4}

---

树上差分

---

序列查分（略）

顾名思义：差分

可以允许的操作：统计若干操作后点（边）被使用（经过了）多少次

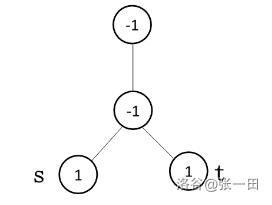
核心：从S走到T，

sum[s]++;
sum[t]++;
sum[LCA(s,t)]--;
sum[fa[LCA(s,t)][0]]--

经典例题：松鼠的新家洛谷P3258

可持久化字典树（Tire）

---

解决问题：异或和问题，求最大异或和
思路：每次在字典树中找相反位

前置题目，用字典树解决最大异或和The XOR-longest Path
因为这道题还是比较巧妙，所以说两句，因为开始我也没想出来怎么用字典树。
因为是一棵树，所以两点之间路径长是固定的，以任意一个点为根DFS遍历整棵树，求出根到每个点的路径长f[ ]，所以问题变成求两个f[ ]异或值最大，用字典树解决。

可持久化字典树核心操作：插入（insert），查询（query）。
上易懂图

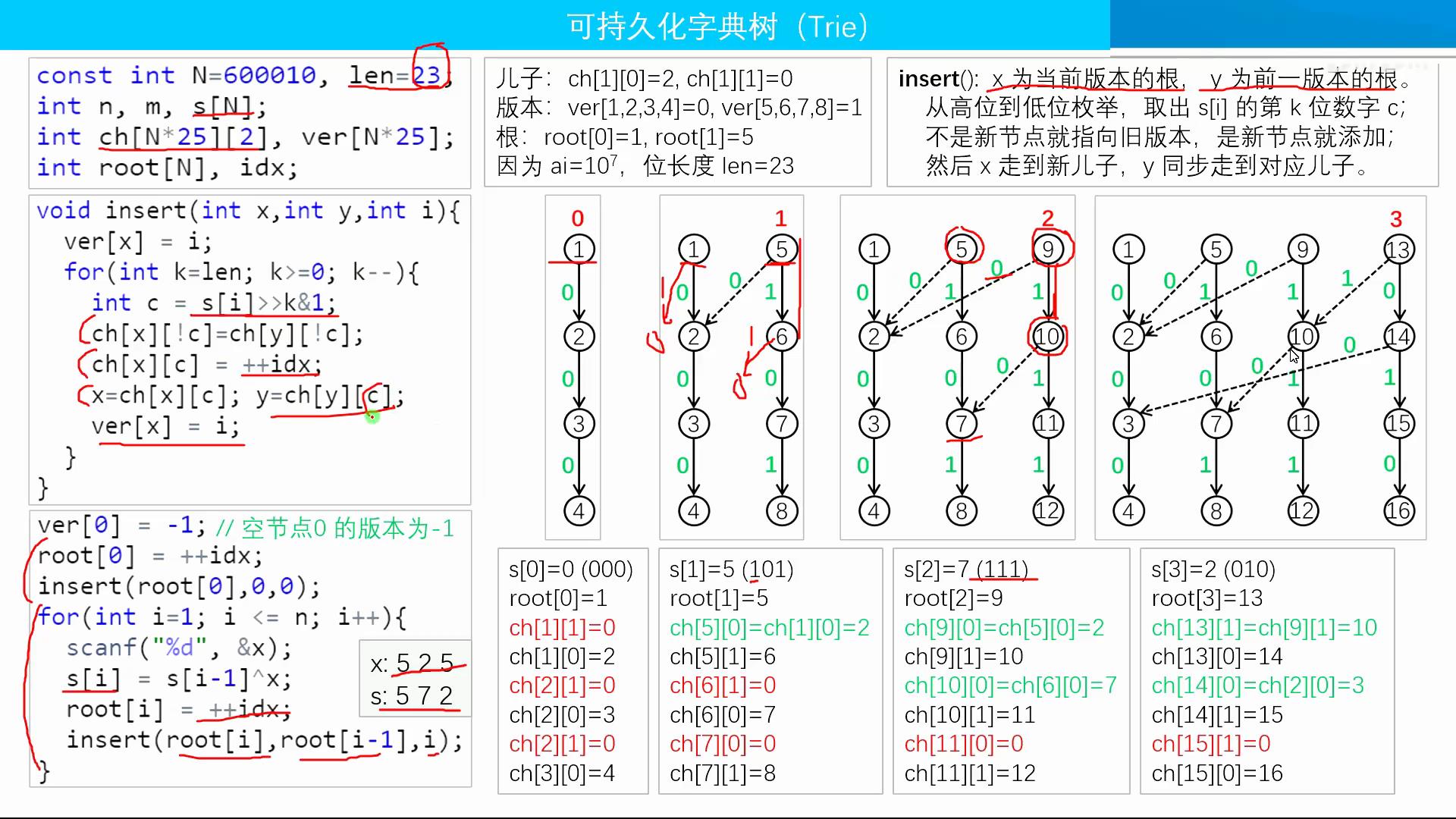
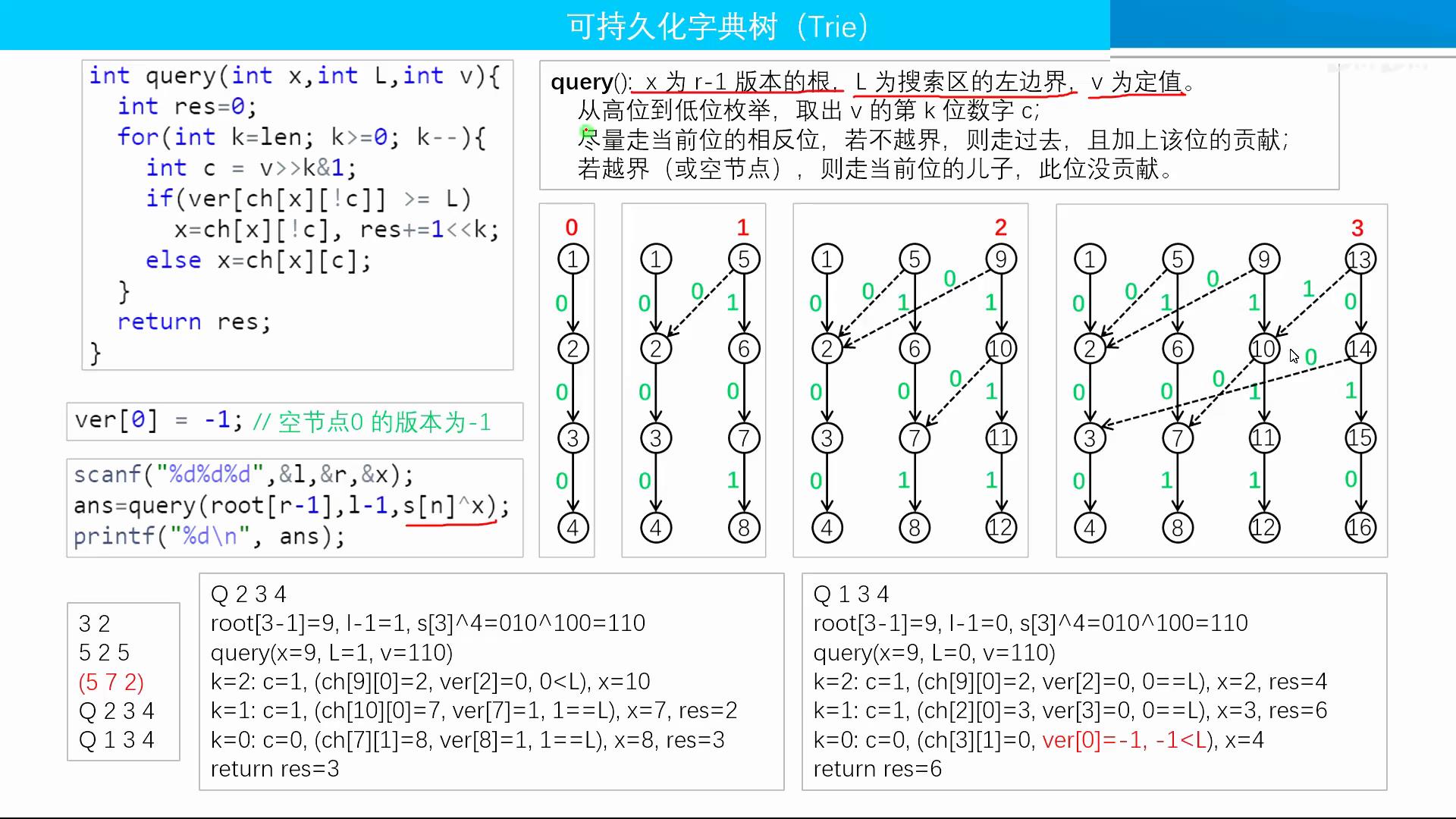
清晰易懂，我甚至感觉我不需要多讲什么了。

---

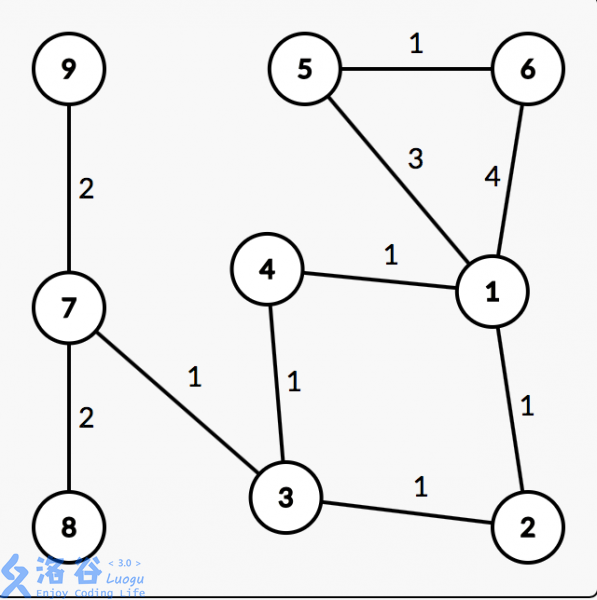
圆方树（仙人掌图）

无向仙人掌图的定义：

任意一条边至多只出现在一条简单回路的无向连通图称为仙人掌。

---

Update日志：

2023.3.25第一次更新了三个知识点
2023.5.1第二次更新了可持久化字典树，并移植到博客园上