Josephus问题：ArrayList实现
编号为1,2,3...n的人一词围成一圈，从第k个人开始报数（从1开始），数到m的人退出。接着下一个人又从1开始报数，数到m的人退出，以此类推。问：剩下的人的编号是多少？
为了更加清晰理解题意，举例说明
编号若为1到7，m为3，那么第一次被去掉的数为4。意思是起点是1，移动了3次，那么移动结束到了4、
ArrayList的listIterator这个迭代器，有三个属性，一个是cursor游标，一个是expectedModCount，一个是lastRet游标移动过程中经过的值。
还有就是要理解cursor游标的位置和元素的位置，游标的位置是元素之间的，特殊的，第一个游标在第一个元素之前，最后一个游标在最后一个元素之后。如图所示，所以游标构造器，如果是无参数的，游标位置在0，如果是有参的，那么参数最大值是list.size()。
理解lastRet，关键在于理解游标的移动过程，迭代器有两个方法next（），和previous（），都会移动游标，返回一个元素。
如果当前游标位置在0，使用了next方法，那么游标位置往后移动到了1，中间经过的元素为1，所以lastRet的值为1，next方法返回值1.
如果当前游标位置在3，使用了previous方法，那么游标位置往前移动到了2，中间经过的元素为3，所以lastRet的值为3，previous方法返回值3.
package three;
import java.util.ArrayList;
import java.util.ListIterator;
public class passGame {
public static void pass(int m, int n)
{
int i, j, mPrime, numLeft;
ArrayList<Integer> L = new ArrayList<Integer>();
for (i=1; i<=n; i++)
L.add(i);
ListIterator<Integer> iter = L.listIterator();
Integer item=0;
numLeft = n;//剩下的个数，初值为数组长度
mPrime = m % n;//为余数
for (i=0; i<n; i++)
{
mPrime = m % numLeft;//游标需要往前移动的次数
if (mPrime <= numLeft/2)//余数小于等于长度的一半
{
if (iter.hasNext())
item = iter.next();//把游标指到第一个人手里，相当于数数前的准备工作
for (j=0; j<mPrime; j++)//再次移动了mPrime次游标
{
if (!iter.hasNext())//如果到达链表最后元素，则回到起点
iter = L.listIterator();
item = iter.next();
}
}
else//余数大于长度的一半（如果这个次数大于长度一半，那么不如从后往前走）
{
for (j=0; j<numLeft-mPrime; j++)
{
if (!iter.hasPrevious())//如果到达了链表开头第一个元素，那么游标放到最后
iter = L.listIterator(L.size());
item = iter.previous();
}
}
System.out.print("Removed " + item + " ");
iter.remove();
if (!iter.hasNext())//如果到达链表最后元素
iter = L.listIterator();//赋值无参数的迭代器，默认游标位置是0
System.out.println();
for (Integer x:L)
System.out.print(x + " ");
System.out.println();
numLeft--;//每次循环后，剩余长度-1
}
System.out.println();
}
public static void main(String[] args) {
// TODO Auto-generated method stub
pass(3,7);
}
}
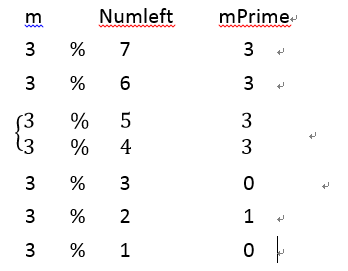
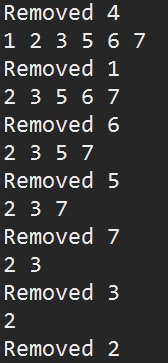
如果m为3，n为7，那么程序运行过程如上左图，只有大括号的两次才进入else，即mPrime大于了Numleft的一半。
程序运行结果如上右图。
m取余numLeft为mPrime，即需要往后走的次数，只有两种情况：
一种是numLeft>m，那么余数就是m（前四行），即剩余长度>m。
另一种是numLeft<=m,那么余数就是小于m的（后三行），即剩余长度<=m，这种情况因为链表剩余长度太短，整个链表会被至少走一遍，而这一遍可以不用走，省略掉。比如，3 % 3 =0，因为剩余长度是3，移动次数也是3，移动完就是第一个元素，所以，就不用移动了，就是0步。
计算完往后走的次数后，还得考虑以下两种情况（是否往前走更快速）：
如果mPrime <= numLeft/2，那么就正常得往后走mPrime次。
如果mPrime <= numLeft/2，那么往后走mPrime次，不如往前走numLeft-mPrime次。
