JAVA实现二项队列
二项队列和其他优先队列的区别在于,它是具有一定顺序的树的集合,即森林。
它具有一个数组,每个数组元素存每棵树,通过存每棵树的根节点的引用。
数组中,0索引的那颗树存1个元素,1索引的那颗树存2个元素,以此类推。
二项队列的设计思想完全利用了二进制的原理。而其中merge函数的switch case判断也是利用二进制的原理。而二项队列中的最重要的操作,合并操作,也可以通过将两个二进制数相加来理解。
插入操作就是特殊的合并。
删除最小功能也可以说是特殊的合并:找到最小元素所在的那棵树,去掉根,这样就分解出了一个森林。
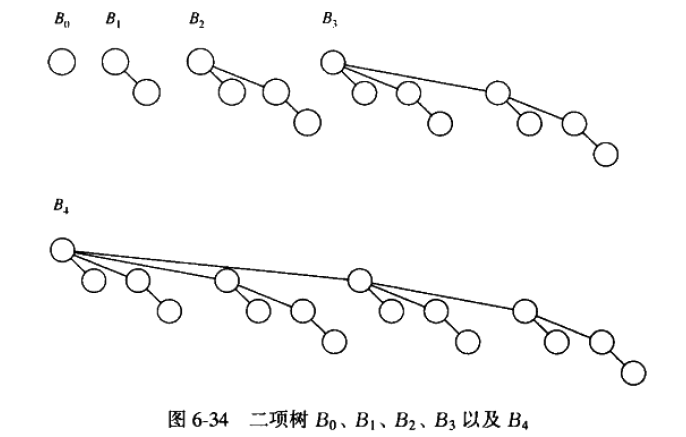
二项树从小到大举例:
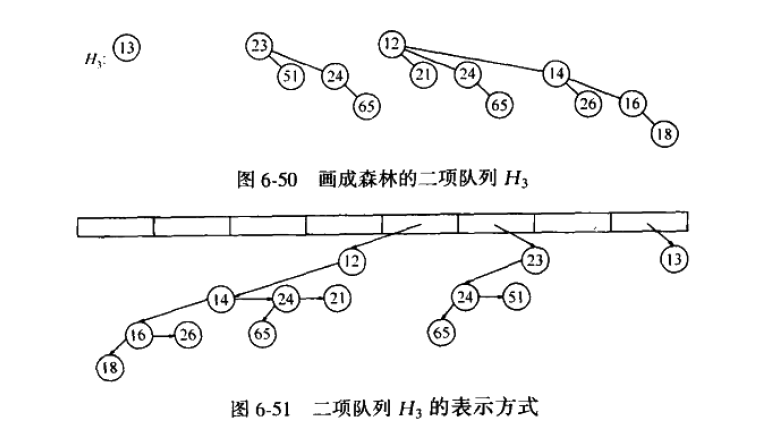
兄弟孩子表示法举例:
代码之后,还有图解,帮助理解。
代码如下,可运行,应该没有错误,注意写的注释才是最重要的,帮助理解:
package six;
// BinomialQueue class
//
// CONSTRUCTION: with no parameters or a single item
//
// ******************PUBLIC OPERATIONS*********************
// void insert( x ) --> Insert x
// Comparable deleteMin( )--> Return and remove smallest item
// Comparable findMin( ) --> Return smallest item
// boolean isEmpty( ) --> Return true if empty; else false
// void makeEmpty( ) --> Remove all items
// vod merge( rhs ) --> Absord rhs into this heap
// ******************ERRORS********************************
// Throws UnderflowException as appropriate
/**
* Implements a binomial queue.
* Note that all "matching" is based on the compareTo method.
* @author Mark Allen Weiss
*/
class UnderflowException extends Exception { };
public final class BinomialQueue<AnyType extends Comparable<? super AnyType>>
{
/**
* Construct the binomial queue.
*/
public BinomialQueue( )
{
theTrees = new BinNode[ DEFAULT_TREES ];//生成了一个node数组,这里有警告是java泛型数组无法创建的问题
//即无法通过普通方法创建泛型数组
makeEmpty( );
}
/**
* Construct with a single item.
*/
public BinomialQueue( AnyType item )
{
currentSize = 1;
theTrees = new BinNode[ 1 ];//生成了一个node数组
theTrees[ 0 ] = new BinNode<>( item, null, null );
}
private void expandTheTrees( int newNumTrees )
{
BinNode<AnyType> [ ] old = theTrees;//获得自身数组的长度
int oldNumTrees = theTrees.length;
theTrees = new BinNode[ newNumTrees ];//将传进来的参数作为新数组的长度
//以下两个循环,如果新长度比旧长度大,那么两个循环都执行,新数组为旧数组加上null元素
//如果小或等于,那么只执行第一个循环,新数组为旧数组除掉后面几个元素
//但是实际只有两个情况,新长度比旧长度大1,或者新长度和旧长度一样,但情况还是上面的两种情况
for( int i = 0; i < Math.min( oldNumTrees, newNumTrees ); i++ )
theTrees[ i ] = old[ i ];
for( int i = oldNumTrees; i < newNumTrees; i++ )
theTrees[ i ] = null;
}
/**
* Merge rhs into the priority queue.
* rhs becomes empty. rhs must be different from this.
* @param rhs the other binomial queue.
*/
public void merge( BinomialQueue<AnyType> rhs )
{
if( this == rhs ) // Avoid aliasing problems
return;
currentSize += rhs.currentSize;//获得size之和
if( currentSize > capacity( ) )//如果size之和大于了从最高位到最低位的树容量之和,即最高位已经不能满足
{//如果进去if,则说明容量不够
int newNumTrees = Math.max( theTrees.length, rhs.theTrees.length ) + 1;
//取二者最高位加1就行,道理同两个四位数加起来最多是个五位数
expandTheTrees( newNumTrees );//扩展树,传的参数是新的森林的树的个数,即最高位是第几位
}
BinNode<AnyType> carry = null;//进位
for( int i = 0, j = 1; j <= currentSize; i++, j *= 2 )//currentSize已经是size之和,如果在j=currentSize结束
//那么就是最高位的那棵树把所有元素都装进去了,别的位都没有树
{
BinNode<AnyType> t1 = theTrees[ i ];//遍历老数组元素,老数组可能被增长
BinNode<AnyType> t2 = i < rhs.theTrees.length ? rhs.theTrees[ i ] : null;//遍历新数组,如果到头,就为null
int whichCase = t1 == null ? 0 : 1; //旧数组元素如果为
whichCase += t2 == null ? 0 : 2;//新数组元素如果为
whichCase += carry == null ? 0 : 4;//进位如果为
switch( whichCase )//充分利用二进制数的原理来判断
{
case 0: /* No trees 双方元素都为空*/
case 1: /* Only this 旧元素有,新元素没有,但没有进位,所以也不需要操作*/
break;
case 2: /* Only rhs 即只有新元素*/
theTrees[ i ] = t2;//把新元素按照位置赋值给旧元素
rhs.theTrees[ i ] = null;
break;
case 4: /* Only carry 只有进位*/
theTrees[ i ] = carry;//把进位赋值按照位置赋值给旧元素
carry = null;
break;
case 3: /* this and rhs 旧元素和新元素,无进位*/
carry = combineTrees( t1, t2 );
theTrees[ i ] = rhs.theTrees[ i ] = null;
break;
case 5: /* this and carry 旧元素和进位*/
carry = combineTrees( t1, carry );
theTrees[ i ] = null;//进位已被赋值,不用清空
break;
case 6: /* rhs and carry 新元素和进位*/
carry = combineTrees( t2, carry );
rhs.theTrees[ i ] = null;
break;
case 7: /* All three 旧元素和新元素和进位都有*/
theTrees[ i ] = carry;
carry = combineTrees( t1, t2 );
rhs.theTrees[ i ] = null;//进位和旧元素已被赋值,不用清空
break;
}
}
for( int k = 0; k < rhs.theTrees.length; k++ )
rhs.theTrees[ k ] = null;//感觉此循环不需要,因为之前循环已经清空了
rhs.currentSize = 0;
//对于以上三行代码,不如直接调用rhs的makeEmpty函数来代替
}
/**
* Return the result of merging equal-sized t1 and t2.
*/
private BinNode<AnyType> combineTrees( BinNode<AnyType> t1, BinNode<AnyType> t2 )
{
if( t1.element.compareTo( t2.element ) > 0 )//比较两个点的大小,递归传递让第一个参数的值更小
return combineTrees( t2, t1 );
t2.nextSibling = t1.leftChild;//根据孩子兄弟表示法来连接链接
t1.leftChild = t2;
return t1;
}
/**
* Insert into the priority queue, maintaining heap order.
* This implementation is not optimized for O(1) performance.
* @param x the item to insert.
*/
public void insert( AnyType x )
{
merge( new BinomialQueue<>( x ) );//调用只有一个元素的构造参数,插入就是特殊的合并
}
/**
* Find the smallest item in the priority queue.
* @return the smallest item, or throw UnderflowException if empty.
*/
public AnyType findMin( ) throws UnderflowException
{
if( isEmpty( ) )
throw new UnderflowException( );//throw到了最终的那个函数,必须有throws
return theTrees[ findMinIndex( ) ].element;//最小元素肯定是某颗树的根
}
/**
* Find index of tree containing the smallest item in the priority queue.
* The priority queue must not be empty.
* @return the index of tree containing the smallest item.
*/
private int findMinIndex( )
{
int i;
int minIndex;
for( i = 0; theTrees[ i ] == null; i++ )//这里意思是找到第一个有树的位置,它有可能是最小位置
;//如果第一位含有树,那么不符合循环条件,i直接=0
for( minIndex = i; i < theTrees.length; i++ )//循环比较,如果更小就更新minIndex
if( theTrees[ i ] != null &&
theTrees[ i ].element.compareTo( theTrees[ minIndex ].element ) < 0 )
minIndex = i;
return minIndex;//返回数组索引,比正常看减一
}
/**
* Remove the smallest item from the priority queue.
* @return the smallest item, or throw UnderflowException if empty.
*/
public AnyType deleteMin( ) throws UnderflowException
{
if( isEmpty( ) )
throw new UnderflowException( );
int minIndex = findMinIndex( );
AnyType minItem = theTrees[ minIndex ].element;
BinNode<AnyType> deletedTree = theTrees[ minIndex ].leftChild;//除了没有根的所有链表
// Construct H''
BinomialQueue<AnyType> deletedQueue = new BinomialQueue<>( );//构造一个新的二项队列
deletedQueue.expandTheTrees( minIndex );//如果是第4位,数组索引是3,扩展到只有三颗树,刚好装下
//因为第4位的那棵树装8个元素,去掉根还有7个,前三棵树的大小=1+2+4=7,刚好装下,不过每个数组元素都是null
deletedQueue.currentSize = ( 1 << minIndex ) - 1;//道理之前讲过
for( int j = minIndex - 1; j >= 0; j-- )//如果是第4位,数组索引是3。从数据结构上看除去根还有三棵树
//三棵树构成数组,数组最大索引为3-1=2,所以minIndex - 1
{
deletedQueue.theTrees[ j ] = deletedTree;//第一次循环肯定是具有儿子最多的那颗子树,所以赋值给最大索引
deletedTree = deletedTree.nextSibling;//把下一个兄弟赋值给deletedTree,为下一次循环做准备
deletedQueue.theTrees[ j ].nextSibling = null;//赋值给数组元素后,每个根就应该没有兄弟链了
}
// Construct H'
theTrees[ minIndex ] = null;//最小根所在的那棵树,已经被分解完毕,则需要赋值为null
currentSize -= deletedQueue.currentSize + 1;//因为deletedQueue少了根,所以再加1就好了
merge( deletedQueue );//合并
return minItem;
}
/**
* Test if the priority queue is logically empty.
* @return true if empty, false otherwise.
*/
public boolean isEmpty( )
{
return currentSize == 0;
}
/**
* Make the priority queue logically empty.
*/
public void makeEmpty( )
{
currentSize = 0;
for( int i = 0; i < theTrees.length; i++ )
theTrees[ i ] = null;
}
private static class BinNode<AnyType>
{
// Constructors
BinNode( AnyType theElement )
{
this( theElement, null, null );
}
BinNode( AnyType theElement, BinNode<AnyType> lt, BinNode<AnyType> nt )
{
element = theElement;
leftChild = lt;//高度最高的儿子节点,正常表示时每个节点有几个儿子,但实际存储时只有一个儿子
nextSibling = nt;//高度略小的兄弟
}
AnyType element; // The data in the node
BinNode<AnyType> leftChild; // Left child
BinNode<AnyType> nextSibling; // Right child
}
private static final int DEFAULT_TREES = 1;
private int currentSize; // # items in priority queue在堆中有多少个元素
private BinNode<AnyType> [ ] theTrees; // An array of tree roots森林的根有多少个,即总能知道最高位是多少
/**
* Return the capacity.
*/
private int capacity( )
{
return ( 1 << theTrees.length ) - 1;//假设最高位为第n位,那么1 << (n-1)就是最高位的那颗树的容量
//但要求的是前n位即n颗树的容量和,所以(1 << n)-1刚好是容量和,根据二进制数的性质
//比如前五位,16-1=8+4+2+1
}
public static void main( String [ ] args ) throws UnderflowException
{
int numItems = 10000;
BinomialQueue<Integer> h = new BinomialQueue<>( );
BinomialQueue<Integer> h1 = new BinomialQueue<>( );
int i = 37;
System.out.println( "Starting check." );
for( i = 37; i != 0; i = ( i + 37 ) % numItems )
if( i % 2 == 0 )
h1.insert( i );//h1全是偶数
else
h.insert( i );//h全是奇数
h.merge( h1 );
for( i = 1; i < numItems; i++ )
if( h.deleteMin( ) == i )//你会发现输入从1开始到9999
System.out.println( "Oops! " + i );
System.out.println( "Check done." );
}
}
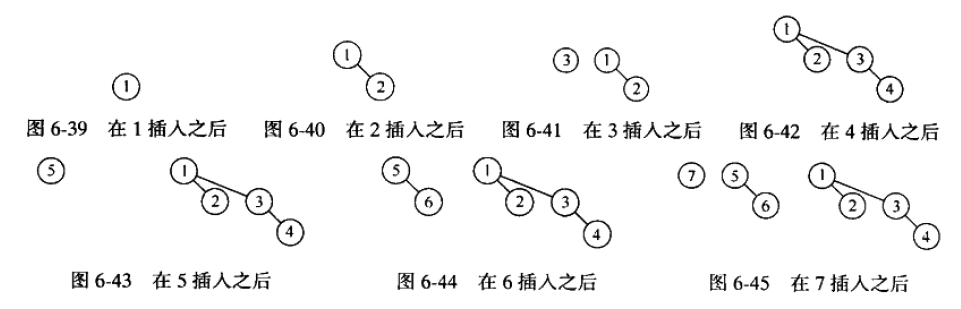
1-8的插入过程:
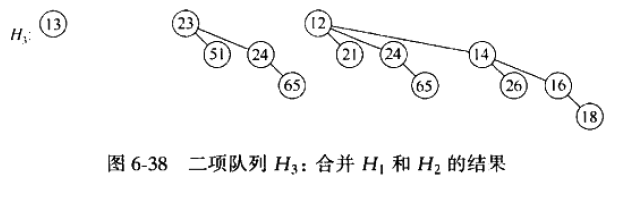
合并两个二项队列的过程:
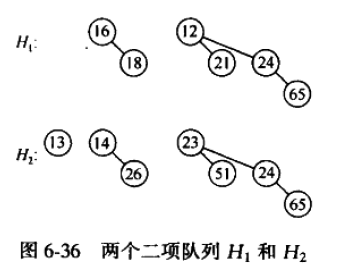
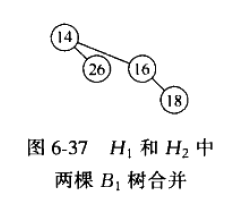
但是最终结果不对,应该说和我代码的过程不一样,因为在代码中,图6-37这颗新树作为进位赋值给carry,在最终结果中,第三个位置即含有4个元素的那棵树应该就是图6-37这颗新树。而最终结果中的那颗包含8个元素的那颗新树应该是由H1和H2中的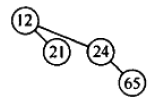
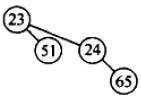
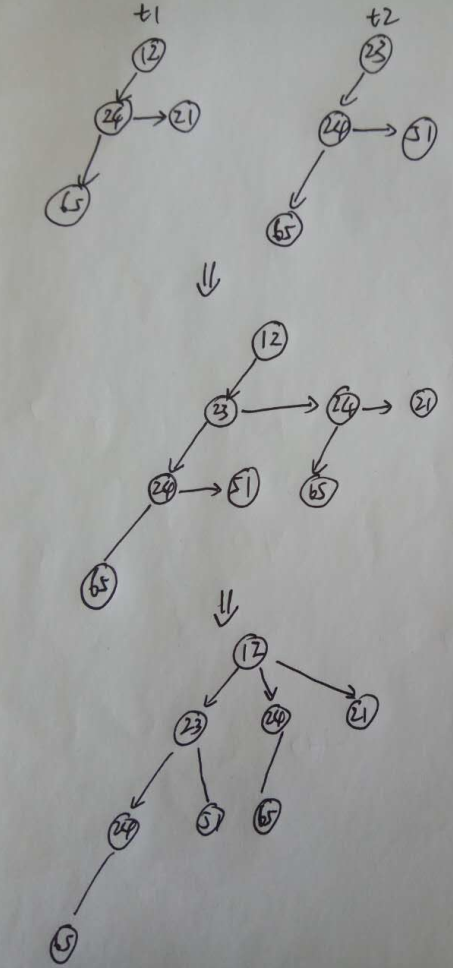
而合并两棵树时的链接变化过程如下(t1,t2——t1根更小):
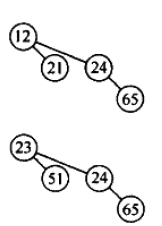
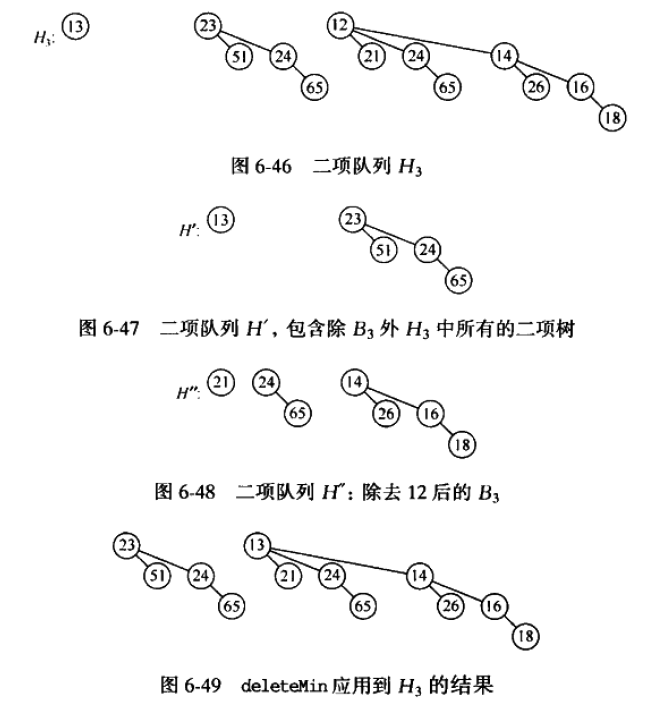
而删除过程如下:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号