phthon3 常见相似度计算
此博客参考了常用的相似度计算方法原理及实现
并将里面的python2代码,改成了python3代码。
1、欧几里得距离(Eucledian Distance)
def Eucledian(x,y):
result = sqrt(sum([pow((a-b),2) for a,b in zip(x,y)]))
return result2、曼哈顿距离(Manhattan Distance)
def Manhattan(x,y):
result = sum([abs(a-b) for a,b in zip(x,y)])
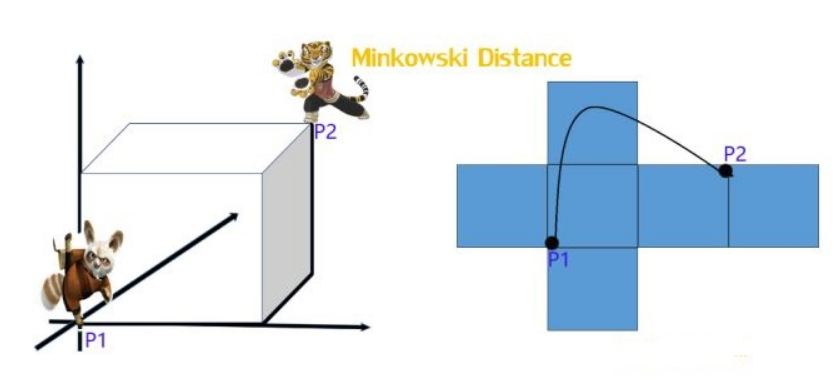
return result3、明可夫斯基距离(Minkowski distance)
公式:
从公式我们可以看出,
- 当p==1,“明可夫斯基距离”变成“曼哈顿距离”
- 当p==2,“明可夫斯基距离”变成“欧几里得距离”
- 当p==∞,“明可夫斯基距离”变成“切比雪夫距离”
def Minkowski(x,y,p):
sumvalue = sum([pow(abs(a-b),p) for a,b in zip(x,y)])
mi = pow(sumvalue,Fraction(1,p))
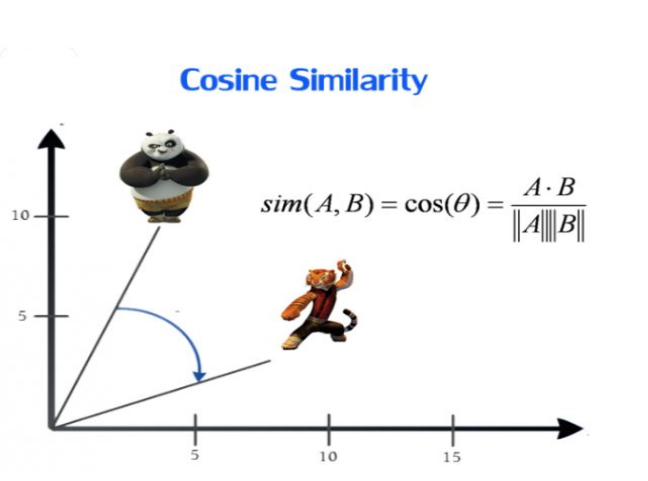
return mi4、(余弦相似度)Cosine Similarity
余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比距离度量,余弦相似度更加注重两个向量在方向上的差异,而非距离或长度上。
def consine_dis(x,y):
dot = sum([a*b for a,b in zip(x,y)])
denom = np.linalg.norm(x) * np.linalg.norm(y)
result = dot/denom
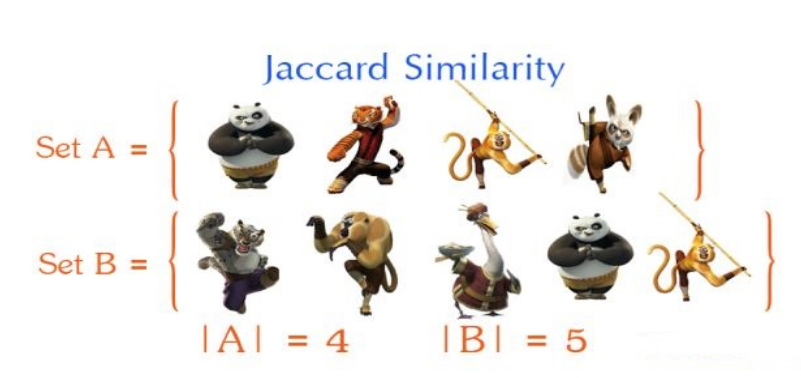
return result5、Jaccard Similarity
Jaccard系数主要用于计算符号度量或布尔值度量的个体间的相似度,因为个体的特征属性都是由符号度量或者布尔值标识,因此无法衡量差异具 体值的大小,只能获得“是否相同”这个结果,所以Jaccard系数只关心个体间共同具有的特征是否一致这个问题。def jaccard(x,y):
intersection = set(x)&set(y)
union = set(x)|set(y)
return len(intersection)/len(union)下面是完整代码:
from math import *
from fractions import Fraction
import numpy as np
def Eucledian(x,y):
result = sqrt(sum([pow((a-b),2) for a,b in zip(x,y)]))
return result
def Manhattan(x,y):
result = sum([abs(a-b) for a,b in zip(x,y)])
return result
def Minkowski(x,y,p):
sumvalue = sum([pow(abs(a-b),p) for a,b in zip(x,y)])
mi = pow(sumvalue,Fraction(1,p))
return mi
print(Eucledian([0,0],[3,4]))
print(Manhattan([0,0],[3,4]))
print(Minkowski([0,0],[3,4],1))
print(Minkowski([0,0],[3,4],2))
def consine_dis(x,y):
dot = sum([a*b for a,b in zip(x,y)])
denom = np.linalg.norm(x) * np.linalg.norm(y)
result = dot/denom
return result
print(consine_dis([0,1],[1,0]))
def jaccard(x,y):
intersection = set(x)&set(y)
union = set(x)|set(y)
return len(intersection)/len(union)
print(jaccard([1,2,3],[1,2,4]))
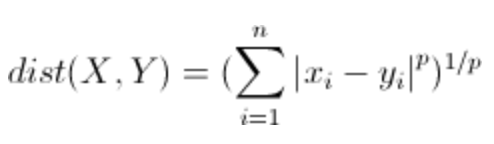

 浙公网安备 33010602011771号
浙公网安备 33010602011771号