Floyd算法详解——证明无后效性——寻找最小环

• 代码
• 原理分析
• 动态规划
• 滚动数组（证明无后效性）
• 一个例子
• 负权边 负权环
• 代码实现
  • 无负权环
  • 有负权环
  • 有负权边但未形成负权环
  • 寻找最小环
  • path二维数组

代码

Floyd算法代码非常简洁，它是一种基于动态规划的多源最短路径算法（即可以求出每个点对之间的最短路径）。
初步分析来看，代码就是个三层嵌套循环，然后就是k层循环在最外层。其实记住这些，就够使用了，但研究算法还是不求甚解比较好。

    private void floyd() {
        for (int k = 0; k < n; k++) {
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    a[i][j] = Math.min(a[i][j], a[i][k] + a[k][j]);
                }
            }
        }

原理分析

假设节点序号是从1到n。
假设f[0][i][j]$f[0][i][j]$是一个n*n的矩阵，第i行第j列代表从i到j的权值，如果i到j有边，那么其值就为ci,j$c_{i,j}$（边ij的权值）。如果没有边，那么其值就为无穷大。

f[k][i][j]$f[k][i][j]$代表（k的取值范围是从1到n），在考虑了从1到k的节点作为中间经过的节点时，从i到j的最短路径的长度。

比如，f[1][i][j]$f[1][i][j]$就代表了，在考虑了1节点作为中间经过的节点时，从i到j的最短路径的长度。

分析可知，f[1][i][j]$f[1][i][j]$的值无非就是两种情况，而现在需要分析的路径也无非两种情况，i=>j，i=>1=>j$i=>j，i=>1=>j$：
【1】f[0][i][j]$f[0][i][j]$：i=>j$i=>j$这种路径的长度，小于，i=>1=>j$i=>1=>j$这种路径的长度
【2】f[0][i][1]+f[0][1][j]$f[0][i][1]+f[0][1][j]$：i=>1=>j$i=>1=>j$这种路径的长度，小于，i=>j$i=>j$这种路径的长度

形式化说明如下：
f[k][i][j]$f[k][i][j]$可以从两种情况转移而来：
【1】从f[k−1][i][j]$f[k-1][i][j]$转移而来，表示i到j的最短路径不经过k这个节点
【2】从f[k−1][i][k]+f[k−1][k][j]$f[k-1][i][k]+f[k-1][k][j]$转移而来，表示i到j的最短路径经过k这个节点

总结就是：f[k][i][j]=min(f[k−1][i][j],f[k−1][i][k]+f[k−1][k][j])$f[k][i][j]=min(f[k-1][i][j],f[k-1][i][k]+f[k-1][k][j])$
从总结上来看，发现f[k]$f[k]$只可能与f[k−1]$f[k-1]$有关。

动态规划

从动态规划的角度分析，题目需要合理的定义状态，划分阶段。

我们定义f[k][i][j]$f[k][i][j]$为考虑从1到k这些节点后，所能得到的最短路径的长度。
f[k][i][j]$f[k][i][j]$可以从f[k−1][i][j]$f[k-1][i][j]$转移而来，表示i$i$到j$j$的最短路径不经过k$k$这个节点。
f[k][i][j]$f[k][i][j]$也可以从f[k−1][i][k]+f[k−1][k][j]$f[k-1][i][k]+f[k-1][k][j]$转移而来，表示i$i$到j$j$的最短路径经过k$k$这个节点。

考虑以上状态的定义，是否满足最优子结构和无后效性原则。
最优子结构：在图中，显而易见，最短路径的子路径仍然是最短路径。比如一条从1到5的最短路径为1=>2=>3=>4=>5，那么1=>2=>3一定是1到3的最短路径，3=>4=>5一定是3到5的最短路径。形式化说明则是，从j到j的最短路径一定是由从i到k的最短路径再合上从k到j的最短路径组成的。

上面这个例子虽然方便理解，但如果要结合Floyd算法和上述例子分析的话，上述例子是把一个有4截的最短路径，分为有2截的最短路径加起来，那么Floyd算法的k层循环则是每次只加1截最短路径。

所谓无后效性原则，指的是这样一种性质：某阶段的状态一旦确定，则此后过程的演变不再受此前各状态及决策的影响。也就是说，“未来与过去无关”，当前的状态是此前历史的一个完整总结，此前的历史只能通过当前的状态去影响过程未来的演变。

无后效性：从上述定义可以看出f[k]$f[k]$的状态完全是从f[k−1]$f[k-1]$转移过来，所以我们只要把k放到最外层循环中，就可以保证无后效性。

滚动数组（证明无后效性）

可以发现，整个程序一直在对同一个二维数组进行操作，而不是因为最外层循环有k层，就建立k个二维数组。这是因为这个二维数组可以在更新的过程一直重复利用，而且按照程序流程走，不会出现错误的情况。
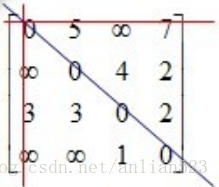
假设初始二维数组f[0]$f[0]$为：

最外层循环k从1开始，f[1][i][j]$f[1][i][j]$只和f[0]$f[0]$有关。
有第一种情况f[1][i][j]$f[1][i][j]$=f[0][i][j]$f[0][i][j]$
和第二种情况f[1][i][j]$f[1][i][j]$=f[0][i][1]+f[0][1][j]$f[0][i][1]+f[0][1][j]$这两种情况。

参与计算的值：指等号右边的值

下面分析在k=1时的最外层循环中：
第一种情况中，参与计算的值就是它本身（因为使用的是同一个二维数组，而ij$ij$又是一样的）（符合无后效性：f[1]$f[1]$的状态完全是从f[0]$f[0]$转移过来）
第二种情况中，参与计算的值由两部分组成f[0][i][1]+f[0][1][j]$f[0][i][1]+f[0][1][j]$。
f[0][i][1]$f[0][i][1]$是第1列元素（i从1变化到4，所以是第1列）且f[0][1][j]$f[0][1][j]$是第1行元素（j从1变化到4，所以是第1行）。
蓝线代表对角线元素。

既然k=1确定下来了，再确定i和j，i和j无非就是下面的情况：
(1,1)(1,2)(1,3)(1,4)(2,1)(2,2)...(4,4)$(1,1)(1,2)(1,3)(1,4)(2,1)(2,2)...(4,4)$
括号内的取值代表(i,j)$(i,j)$。且循环是按照上面的情况，依次顺序执行。

那么k=1层循环中的某个时刻，这个二维数组的元素有的是属于f[1]$f[1]$的，有的是属于f[0]$f[0]$。比如，有可能是(1,1)(1,2)(1,3)(1,4)$(1,1)(1,2)(1,3)(1,4)$元素是属于f[1]$f[1]$的，(2,1)(2,2)...(4,4)$(2,1)(2,2)...(4,4)$是属于f[0]$f[0]$。因为循环还没有执行完毕嘛。

现在需要做的证明是，因为有f[1]$f[1]$的状态完全是从f[0]$f[0]$转移过来，所以当你计算任意的f[1][i][j]$f[1][i][j]$的过程中，参与计算的值应该是都属于f[0]$f[0]$的，而不是属于f[1]$f[1]$的（即证明无后效性）。

为了证明，现作证明的准备，分析上面提到的第二种情况中参与计算的值的组成的两部分f[0][i][1]+f[0][1][j]$f[0][i][1]+f[0][1][j]$，假设(i,j)$(i,j)$现在确定下来为(2,3)$(2,3)$（且这里假设符第二种情况），那么有f[1][2][3]=f[0][2][1]+f[0][1][3]$f[1][2][3]=f[0][2][1]+f[0][1][3]$

但由于程序是顺序执行的，(2,1)$(2,1)$和(1,3)$(1,3)$肯定是在(2,3)$(2,3)$之前就执行了，意思就是现在我们已经找不到f[0][2][1]$f[0][2][1]$和f[0][1][3]$f[0][1][3]$的值，因为已经被f[1][2][1]$f[1][2][1]$和f[1][1][3]$f[1][1][3]$覆盖掉了啊，既然如此，再按照f[1][2][3]=f[0][2][1]+f[0][1][3]$f[1][2][3]=f[0][2][1]+f[0][1][3]$计算，实际是计算的是f[1][2][3]=f[1][2][1]+f[1][1][3]$f[1][2][3]=f[1][2][1]+f[1][1][3]$，那岂不是违背了我们要做的证明（即无后效性）。

但其实并没有违背，因为f[0][2][1]$f[0][2][1]$和f[1][2][1]$f[1][2][1]$是一样的，同样，f[0][1][3]$f[0][1][3]$和f[1][1][3]$f[1][1][3]$也是一样的。因为f[1][2][1]=f[0][2][1]+f[0][1][1]$f[1][2][1]=f[0][2][1]+f[0][1][1]$，但f[0][1][1]=0$f[0][1][1]=0$（图中对角线的元素都为0），所以就有，实际计算的f[1][2][3]=f[1][2][1]+f[1][1][3]$f[1][2][3]=f[1][2][1]+f[1][1][3]$并不违背无后效性。

进一步分析推广，得出，在红线上的元素对于f[1][i][j]=f[0][i][j]$f[1][i][j]=f[0][i][j]$永远成立。

证明准备完毕，继续证明。情况无非两种，第一种情况和第二种情况。
第一种情况：f[1][i][j]=f[0][i][j]$f[1][i][j]=f[0][i][j]$，等号左边的元素的都是k=1，等号右边的元素都是k=0，符合证明。
第二种情况：f[1][i][j]=f[0][i][1]+f[0][1][j]$f[1][i][j]=f[0][i][1]+f[0][1][j]$.参与计算的值的左边元素和右边元素，都是属于红线上的元素，根据上述证明的准备，得知参与计算的值的元素不管有没有被覆盖掉（从f[0]$f[0]$变到f[1]$f[1]$）,其值与f[0]$f[0]$相等，即不变。即等号右边的元素都是k=0，符合证明。

所以，只用一个二维数组，即滚动数组，是可以的。因为就算反复只用一个数组，计算值的过程中，也一直保持了正确性，即保持了无后效性。
同理分析k=2，k=3，k=4时的最外层循环，也同样能证明在程序运行的过程中，保持了无后效性。

一个例子

假设节点现在从1到5。然后现在已知，1到5的最短路径为1=>4=>3=>2=>5.
现在把重点放在1和5，让i=1，j=5.
最外层循环k从k=1循环到k=5，现在我们只关注每层k循环里面对从1到5的最短路径作了什么贡献：
【1】当k=1时，即考虑中间经过为[1]，没有贡献
【2】当k=2时，即考虑中间经过为[1,2]，虽然没有直接得出1到5的最短路径，但记录下来了从2到5的最短路径
【3】当k=3时，即考虑中间经过为[1,2,3]，虽然没有直接得出1到5的最短路径，但记录下来了从3到5的最短路径
【4】当k=4时，即考虑中间经过为[1,2,3,4]，虽然没有直接得出1到5的最短路径，但记录下来了从4到5的最短路径
【5】最终找到最短路径
这个过程就好比是一个双向搜索的过程，从两端向中间搜索。这个也跟最优子结构有关，最短路径的子路径必定也为最短路径。

负权边 负权环

负权边：权重为负数的边。
负权环：源点到源点的一个环，环上权重和为负数。

Floyd算法只能在不存在负权环的情况下使用。如果有负权环，那么最短路径将无意义，因为我们可以不断走负权环，这样最短路径值便成为了负无穷。但可以处理带负权边但是无负权环的情况。

代码实现

无负权环

length =5
value = [[float("inf") for i in range(length)] for j in range(length)]
for i in range(length):
    value[i][i] = 0

path = [[-1 for i in range(length)] for j in range(length)]
#print(value)
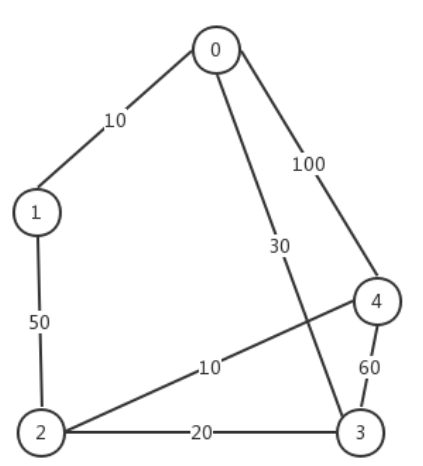
value[0][1] = 10
value[1][0] = 10
value[0][3] = 30
value[3][0] = 30
value[0][4] = 100
value[4][0] = 100
value[1][2] = 50
value[2][1] = 50
value[2][3] = 20
value[3][2] = 20
value[2][4] = 10
value[4][2] = 10
value[3][4] = 60
value[4][3] = 60
for k in range(length):
    for i in range(length):
        for j in range(length):
            temp = value[i][k] + value[k][j]
            if(temp < value[i][j]):
                value[i][j] = temp
                path[i][j] = k
print(value)
print(path)
def get(i,j):
    print('从'+str(i)+'到'+str(j)+'的最短路径长度为'+str(value[i][j]))
    def recursion(i,j):
        if(path[i][j]==-1):#终点
            return ' ' + str(i) + '=>' + str(j) + ' '
        else:
            k = path[i][j]
            return recursion(i,k)+recursion(k,j)
    print(recursion(i,j))
get(1,4)

有负权环

原图为无向图，现改一个边，从2到4的边改为-70，从4到2的边还是不变，这样原图就变成了一个有向图。
所以，2=>4=>2已经构成了一个负权环，其和为-60.
注意3=>2=>4=>2=>3是负权环，其和为-20.

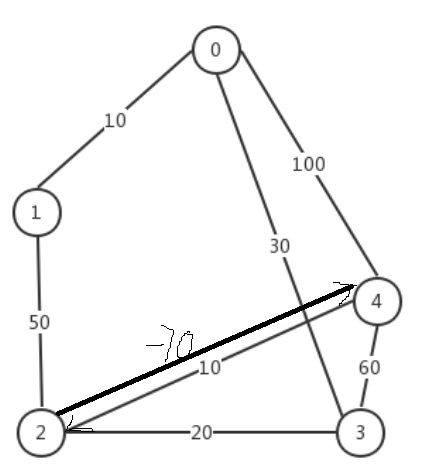
代码改成value[2][4] = -70，改这一行就行。运行结果为：


报错原因：因为path[1,4]的值为4，所以执行递归函数时一直会recursion(1,4)，一直到超出递归次数限制。此时为什么程序输出1=>4的最短路径为-80，是因为1=>4的最短路径为1=>3=>2=>4=>2=>4=30+20-70+10-70=-80。但此时path二维数组已经失去了它的作用，不能用来找到上一个节点，因为负权环的存在。
通过value二维数组的值，可以判断出哪些点构成了负权环，对角线元素本来应该为0，但由于有了负权环，就有value[2][2],value[3][3],value[4][4]不为0，所以就是2,3,4这三个节点构成了负权环的节点。

通过判断对角线元素，可以得出，负权环的构成节点。

有负权边但未形成负权环

代码改成value[0][1] = -10，get(0,4)。此时没有形成负权环。运行结果为：

只要没有形成负权环，那么程序就不会出错。

寻找最小环

环即一条路径的起点和终点是同一个点。
之前的代码，令value的对角线元素的初值为0，现如果将所有节点的初值都设为无穷大，那么在get(i,i)（起点终点为同一个点）时，就能获得从i到i的最小环，因为如果没有环，那么从i到i的路径长肯定还是为float("inf")，但如果有环，则肯定value[i][i]的值肯定会被替换，而且在k的循环中，更小的环会替换掉旧的环，所以，通过这样，可以获得最小环。
我们甚至可以通过，在每k层循环中，检测对角线元素，一旦发现不为float("inf")，便打印出当前形成的环。这样就能得到所有的环了。

length =5
value = [[float("inf") for i in range(length)] for j in range(length)]
#这里不需要令对角线元素为0
path = [[-1 for i in range(length)] for j in range(length)]
value[0][1] = 10
value[1][0] = 10
value[0][3] = 30
value[3][0] = 30
value[0][4] = 100
value[4][0] = 100
value[1][2] = 50
value[2][1] = 50
value[2][3] = 20
value[3][2] = 20
value[2][4] = 10
value[4][2] = 10
value[3][4] = 60
value[4][3] = 60
for k in range(length):
    for i in range(length):
        for j in range(length):
            temp = value[i][k] + value[k][j]
            if(temp < value[i][j]):
                value[i][j] = temp
                path[i][j] = k
print(value)
print(path)
def get(i,j):
    print('从'+str(i)+'到'+str(j)+'的最短路径长度为'+str(value[i][j]))
    def recursion(i,j):
        if(path[i][j]==-1):#终点
            return ' ' + str(i) + '=>' + str(j) + ' '
        else:
            k = path[i][j]
            return recursion(i,k)+recursion(k,j)
    print(recursion(i,j))
get(0,0)

我这个例子不够好，导致能找到的最小环都是只有两个节点的，读者可以自行设计例子，同样能够找出最小环。

path二维数组

这个二维数组的功能是用来记录最短路径中间经过的节点。它有两种赋初值方式：
1.path = [[-1 for i in range(length)] for j in range(length)]
如果是这样的赋初值，那么recursion函数的终点应为if(path[i][j]==-1)
2.path = [[i for i in range(length)] for j in range(length)]
如果是这样的赋初值，那么recursion函数的终点应为if(path[i][j]==j)
即为：