Bellman-ford算法详解——负权环分析
算法描述
输入:图(V,E)和起点original
输出:从original到其他任意节点的最短路径(长度和最短路径构成)
附上两个友情链接:programiz bellman-ford,geeksforgeeks bellman-ford
适用条件
Bellman-ford算法适用于单源最短路径,图中边的权重可为负数即负权边,但不可以出现负权环。
负权边:权重为负数的边。
负权环:源点到源点的一个环,环上权重和为负数。
算法复杂度:O(VE)
算法步骤
dist[]:从original到其他顶点的最短路径长初始为无穷大,自然地,从original到original的距离为0。代表从original到各个顶点的最短路径长度。
pre[]:代表该点在最短路径中的上一个顶点。
1.初始化:除了起点的距离为0外(dist[original] = 0),其他均设为无穷大。
2.迭代求解:循环对边集合E的每条边进行松弛操作,使得顶点集合V中的每个顶点v的距离长逐步逼近最终等于其最短距离长;
3.验证是否负权环:再对每条边进行松弛操作。如果还能有一条边能进行松弛,那么就返回False,否则算法返回True
代码实现
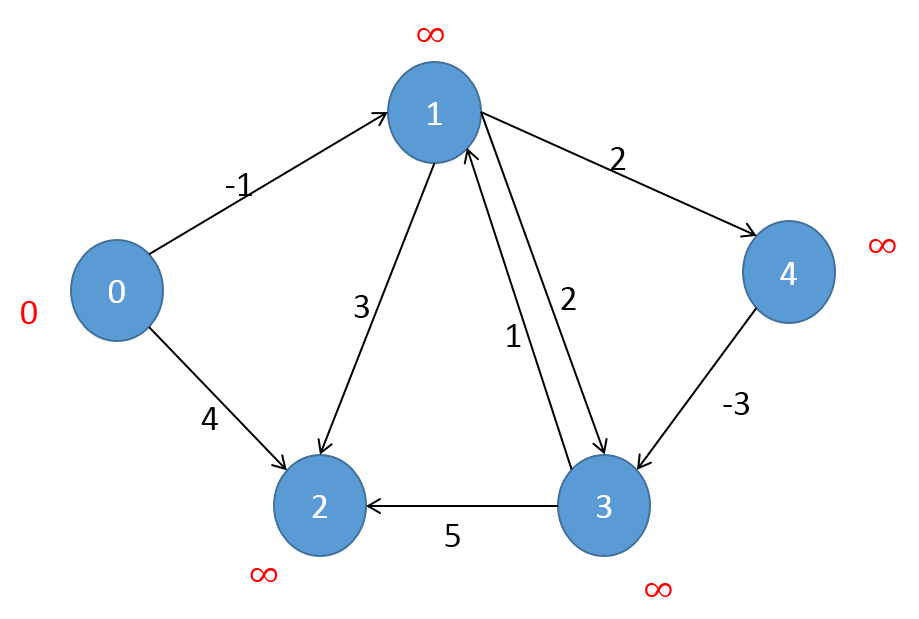
使用如图所示的图结构,其中红色数字代表从起点到各顶点的最短路径长。令0作为起点。
class Edge():
def __init__(self,u,v,cost):
self.u = u
self.v = v
self.cost = cost
nodenum = 5
edgeList = []
dis = [float("inf")]*nodenum
pre = [-1]*nodenum
edgeList.append(Edge(0,1,-1))
edgeList.append(Edge(1,2,3))
edgeList.append(Edge(3,1,1))
edgeList.append(Edge(1,3,2))
edgeList.append(Edge(1,4,2))
edgeList.append(Edge(0,2,4))
edgeList.append(Edge(3,2,5))
edgeList.append(Edge(4,3,-3))
edgenum = len(edgeList)
original = 0
def Bellman_Ford(original):
#令起点到自身的距离为0
for i in range(nodenum):
if(i == original):
dis[i] = 0
print(dis,'\n')
for i in range(nodenum-1):
for j in range(edgenum):
if(dis[edgeList[j].v] > dis[edgeList[j].u] + edgeList[j].cost):
dis[edgeList[j].v] = dis[edgeList[j].u] + edgeList[j].cost
pre[edgeList[j].v] = edgeList[j].u
print('dis',dis)
print('pre',pre,'\n')
flag = True
for i in range(edgenum):
if(dis[edgeList[i].v] > dis[edgeList[i].u] + edgeList[i].cost):
flag = False
break
return flag
print(Bellman_Ford(original))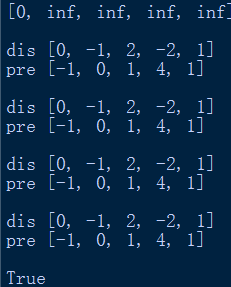
运行结果如上。
算法分析
Bellman_Ford函数里最重要的就是那个双重循环(迭代求解)。
外层循环只nodenum-1次,因为最短路径就算包括所有顶点(这些顶点肯定是不重复的),那么边最多也就有nodenum-1个。而外层循环在算法中的含义就是,每执行一次外层循环,那么便最短路径的边的个数加1,所以外层循环只nodenum-1次。
内层循环代表,从当前记录的最短路径信息之上,继续记录新的最短路径信息(当然,信息也可能维持不变,因为之前的信息已经找到了最短路径)。
而验证是否负权环时,考虑两种情况:
1.负权环的节点个数小于nodenum
2.负权环的节点个数等于nodenum
第一种情况下,在迭代求解的双重循环中,在外层循环的某一层循环开始,负权环对程序就会已经开始错误的影响了。比如,到一个顶点的最短路径长,从那次循环执行完毕后,每次循环都在减小,每次减小负权环的权值和。并且,从那次循环执行完毕后,pre数组会出现环,因为pre数组寻找最短路径是找到-1才停下来,但由于负权环,利用pre数组寻找之前顶点会永远找不到-1(而是会陷入一个环中)。
第二种情况下,在迭代求解的双重循环执行完毕,都不会出现负权环,但由于这种情况下,是有包括所有节点的负权环,包括所有节点的负权环必定有nodenum条边,但之前的迭代求解只执行nodenum-1次(外层循环的次数),那么再执行一次,就能暴露出这个包括所有节点的负权环。
一般情况下,负权环的节点个数小于nodenum。
边的处理顺序
从上述代码中,可以发现迭代求解的第一层外层循环就已经求解出了所有最短路径了,但程序还是循环了4次,但就算这样,循环4次也是必须的。
出现上述这种“浪费时间”的情况,是因为由于,边的处理顺序是最佳顺序,意思就是,每记录一次最短路径的信息,就为下一次记录最短路径信息作好了准备,以至于在第一次外层循环中,就把所有最短路径都记录下来。
如果我们稍微改变一下,边的顺序,就会发现程序在第一次迭代求解中(第一层外层循环),还没有记录下来所有的最短路径信息。
改变边的顺序如下:
edgeList.append(Edge(1,4,2))
edgeList.append(Edge(0,2,4))
edgeList.append(Edge(3,2,5))
edgeList.append(Edge(3,1,1))
edgeList.append(Edge(1,3,2))
edgeList.append(Edge(4,3,-3))
edgeList.append(Edge(0,1,-1))
edgeList.append(Edge(1,2,3))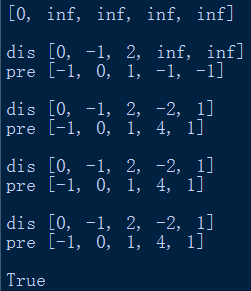
因为例子的原因,没有达到,直到最后一次迭代求解执行完毕才记录下来所有的最短路径信息,的效果。
负权环
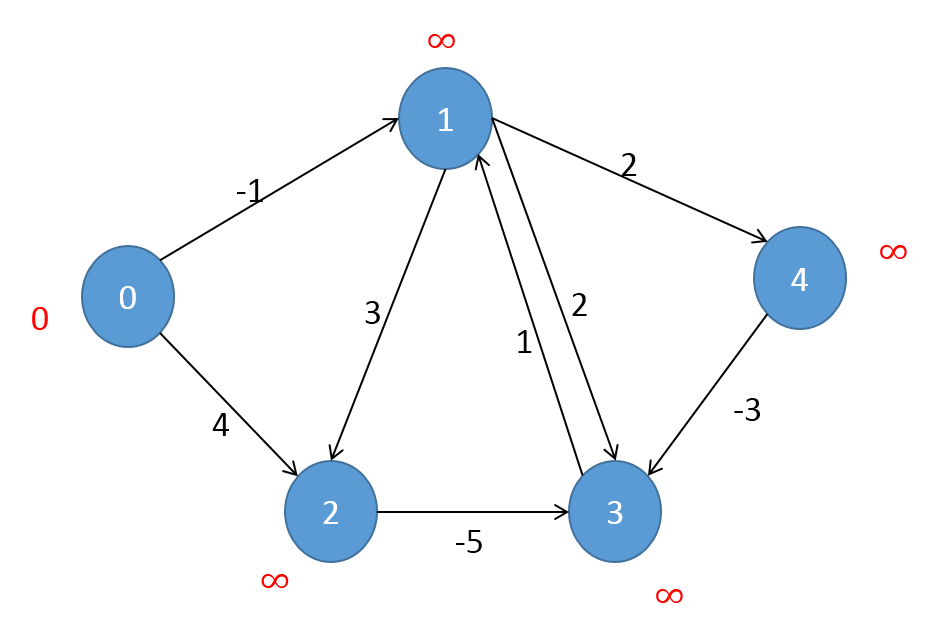
对原例子修改一条边,2和3之间的边改成,方向从2到3,权值为-5。这样123就形成了一个负权环,而且这种负权环属于:负权环的节点个数小于nodenum。
edgeList.append(Edge(0,1,-1))
edgeList.append(Edge(1,2,3))
edgeList.append(Edge(3,1,1))
edgeList.append(Edge(1,3,2))
edgeList.append(Edge(1,4,2))
edgeList.append(Edge(0,2,4))
#edgeList.append(Edge(3,2,5))
edgeList.append(Edge(2,3,-5))
edgeList.append(Edge(4,3,-3))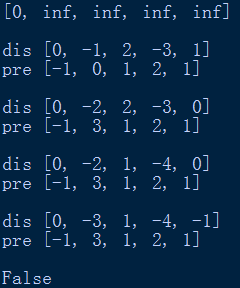
从运行结果可知,从第二次迭代求解开始,dis和pre数组就开始错误了。
比如,出现[-1, 3, 1, 2, 1] 中的这种312的死循环(使用如下代码的get函数,只要参数为3,1,2中的其中一个,那么get内的递归函数就会一直递归,因为到达不了递归终点,最终超过递归次数限制),利用pre数组来找最短路径就会无限循环了。
比如,从第二次迭代求解开始,dis数组的某个值会减小,减去的数都是负权环的和-1。
得到最短路径
利用递归,从终点找到起点。
def get(i):
print('从'+str(original)+'到'+str(i)+'的最短路径为'+str(dis[i]))
def recursion(i):
if(i == -1):
return ''
result = str(i)
return recursion(pre[i])+'=>'+result
print(recursion(i))
get(3)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号