有向图检测环——普通方法、着色法
Detect Cycle in a Directed Graph
未优化
给定有向图如上,环是[1,3,4]。
思路:分别对每个点进行深度遍历,在遍历的过程中,一旦发现当前要存入的元素已经在祖先数组中时,就发现环了,此时打印。当没有打印结果时就代表没有环。
from collections import defaultdict
d = defaultdict(list)#默认值为list的dict
#当做邻接表来使用
d[0] = [1,2]
d[1] = [3]
d[2] = [4]
d[3] = [4]
d[4] = [1]
def recursion(temp):
li = d[temp[-1]]
if(not li):
return
for i in li:
if(i not in temp):
temp.append(i)
recursion(temp)
temp.remove(i)
else:
print(temp)
return
temp = []#深度递归中间变量,存遍历过的祖先
for key in d:
temp.append(key)
recursion(temp)
temp.remove(key)
运行结果如上,每次打印结果都包含[1,3,4]三个元素,也说明了环是[1,3,4],但要知道环到底是哪几个元素,还得需要有个前驱数组(存每个数的前驱)。
优化后
但我现在觉得现在发现环后,下一次循环就不需要再执行了,所以就加个标志位在循环里判断。改进代码如下:
from collections import defaultdict
d = defaultdict(list)#默认值为list的dict
#当做邻接表来使用
d[0] = [1,2]
d[1] = [3]
d[2] = [4]
d[3] = [4]
d[4] = [1]
flag = False
def recursion(temp):
global flag
li = d[temp[-1]]
if(not li):
return
for i in li:
if(i not in temp):
temp.append(i)
recursion(temp)
temp.remove(i)
else:
print(temp)
flag = True
return
temp = []#深度递归中间变量,存遍历过的祖先
for key in d:
if(flag == True):
break
temp.append(key)
recursion(temp)
temp.remove(key)
运行结果如上,只打印了第一次循环的。但实际上,这里还是有多余的执行(打印了两行就能看出,在打印第一行就已经检测到环了),完美的解决方案在下面。
geeksforgeeks的代码
geeksforgeeks有给出了另一种设计方法,虽然基本思路都是一样的。但原代码有两个数组visited和recStack,前者代表是否被访问过,后者代表是否在递归栈中,但实际上只需要后者就行,所以对原代码进行了改动(只留下recStack数组)。
from collections import defaultdict
class Graph():
def __init__(self,vertices):
self.graph = defaultdict(list)
self.V = vertices
def addEdge(self,u,v):
self.graph[u].append(v)
def isCyclicUtil(self, v, recStack):
# Mark current node as visited and
# adds to recursion stack
recStack[v] = True
# Recur for all neighbours
# if any neighbour is visited and in
# recStack then graph is cyclic
for neighbour in self.graph[v]:
if recStack[neighbour] == False:
if self.isCyclicUtil(neighbour, recStack) == True:
return True
elif recStack[neighbour] == True:
return True#递归终点之一,代表找到环
#如果没有环,那么以上循环会以递归树执行,而且不会return,所以会返回下面的终点
# The node needs to be poped from
# recursion stack before function ends
recStack[v] = False
return False#递归终点之一,代表没有环
# Returns true if graph is cyclic else false
def isCyclic(self):
recStack = [False] * self.V
for node in range(self.V):
if self.isCyclicUtil(node,recStack) == True:#为真代表有环
return True
return False
g = Graph(5)
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 3)
g.addEdge(4, 1)
g.addEdge(2, 4)
g.addEdge(3, 4)
if g.isCyclic() == 1:
print ("Graph has a cycle")
else:
print ("Graph has no cycle")
看完这个代码,才知道原来还可以这么设计递归(又是个国外大佬==)。
分析思路:
以0作为起点的递归为例,如果没有环,那么在每个递归分支的末端,在递归末端的这个节点肯定没有邻居了,那么递归函数体内循环根本不会执行,直接返回后面那个递归终点即False,这个结果会返回到这句if self.isCyclicUtil(neighbour, recStack) == True(返回到上一层递归了),不符合条件所以继续向下执行完这层递归没有执行完的部分(由于深度递归,每层递归都会留下后半截没有执行,然后等着程序回溯回来执行后半截),执行后半截又会返回后一个终点,程序又会继续返回到上一层递归。这么一直重复直到执行所有的递归分支。
需要强调,最后返回的False,是第一层递归自己的后一个终点的False,而不是递归回溯时一层一层返回来的False。其实也是,每一层递归返回的False,都是它自己递归层后一个终点的False,而不是它深度递归返回的False。
根据上一段的解释,所以递归内部就不能直接return self.isCyclicUtil(neighbour, recStack),因为这样程序就不能回溯了。那么每次也就无法执行完所有分支了。
以0作为起点的递归为例,如果有环,那么当检测到环时,从最后一层开始时,逐层返回true,一直到最后一层返回true,而且每层递归都不会执行后半截,因为直接return了。
总结:如果没有检测到环,就会继续执行直到完成所有递归分支;当检测到环时,就会一层一层直接return true,不会再执行多余的分支。
geeksforgeeks的原版代码
2019.2.23新增。
这才是原版代码,上一章的代码由于删除掉了visited数组,会导致代码会多做不需要的深度遍历。多亏评论区一位博友的提醒。
from collections import defaultdict
class Graph():
def __init__(self,vertices):
self.graph = defaultdict(list)
self.V = vertices
def addEdge(self,u,v):
self.graph[u].append(v)
def isCyclicUtil(self, v, visited, recStack):
# visited数组元素为true,标记该元素被isCyclicUtil递归调用链处理中,或处理过
# recStack数组元素为true,表示该元素还在递归函数isCyclicUtil的函数栈中
visited[v] = True
recStack[v] = True
# 深度遍历所有节点。
for neighbour in self.graph[v]:
if visited[neighbour] == False: # 如果该节点没有被处理过,那么继续调用递归
if self.isCyclicUtil(neighbour, visited, recStack) == True: # 如果邻接点neighbour的递归发现了环
return True # 那么返回真
elif recStack[neighbour] == True: # 如果neighbour被处理中(这里强调了不是处理过),且还在递归栈中,说明发现了环
return True
recStack[v] = False # 函数开始时,V节点进栈。所以函数结束时,V节点出栈。
return False # v的所有邻接点的递归都没有发现环,则返回假
# 如果该图有环,返回真;否则假
def isCyclic(self):
visited = [False] * self.V
recStack = [False] * self.V
for node in range(self.V): # 分别以每个节点作为起点,然后开始深度遍历
if visited[node] == False: # 这里为真,说明之前的深度遍历已经遍历过该节点了,且那次遍历没有发现环
if self.isCyclicUtil(node,visited,recStack) == True: #如果发现环,直接返回
return True
return False #如果分别以每个节点作为起点的深度遍历都没有发现环,那肯定是整个图没有环
g = Graph(4)
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 2)
g.addEdge(2, 0)
g.addEdge(2, 3)
g.addEdge(3, 3)
if g.isCyclic() == 1:
print "Graph has a cycle"
else:
print "Graph has no cycle"
注释写得很详细了,讲讲重要的点吧:
visited数组元素,只有进入递归函数,就会置为true,且不会复原。这恰好就是visited数组元素的含义,代表着该节点正在递归函数的递归调用过程中,又或者,在之前的递归调用过程已经被处理过(isCyclic函数的之前某一次循环)。recStack数组元素,代表着,递归函数开始时,V节点进栈(visited[v] = True)。所以递归函数结束时,V节点出栈(recStack[v] = False)。所以整个递归调用过程开始前,recStack数组全为False;整个递归调用过程结束后,recStack数组也全为False。- 递归过程中,如果这次递归调用不会发现环,那么邻接点的recStack应该是False。
- isCyclic函数的循环里的
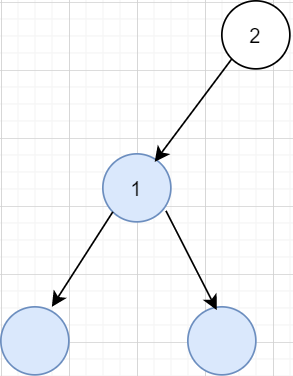
if visited[node] == False:判断,其实和下图的意思一样:假设上一次循环从1节点开始深度遍历,且没有发现环,这会使得1和1的所有儿孙的visited数组都被标记为True,如果这次循环从1的左孩子开始,由于visited为True,不会到这个if分支。
- isCyclicUtil递归函数里的
if visited[neighbour] == False:分支和elif recStack[neighbour] == True:分支,还是看上图,假设递归函数传入的V是2节点,这里会判断2的所有邻居,会发现2的邻居1,这个1它visited为True,但recStack为False,所以这两个分支都不会进入。意思就是,之前的递归过程已经发现从1开始的深度遍历并不会发现环,所以这里不需要从1开始继续深度遍历了。 - isCyclicUtil递归函数里的
elif recStack[neighbour] == True:分支,进入这个分支说明,该邻居visited为True,且recStack为True。看下图,只要是从3、4、5、6开始的深度遍历,在递归调用过程中,最终都会发现这种情况。而且在发现环的情况,visited被设置为True的时机,肯定是在此次递归关联的整个递归调用链中被设置的,而不可能是以前的递归调用链中被设置的。

Detect Cycle in a directed graph using colors
着色法。此方法和上面方法类似(递归设计方法一样),只是数组不再只有两种状态(真或假,代表是否在递归栈中),而是有三种状态(白,灰,黑三种颜色)。代码来自geeksforgeeks,但有个错误,就是每次循环都得初始化color数组(都变为white),我给改过来了。
WHITE : Vertex is not processed yet. Initially
all vertices are WHITE.
GRAY : Vertex is being processed (DFS for this
vertex has started, but not finished which means
that all descendants (ind DFS tree) of this vertex
are not processed yet (or this vertex is in function
call stack)
BLACK : Vertex and all its descendants are
processed.
While doing DFS, if we encounter an edge from current
vertex to a GRAY vertex, then this edge is back edge
and hence there is a cycle.
白色代表此节点还没有被处理。
灰色代表此节点正在被处理,或者说他的儿孙们还没有被处理,或者说它当前这层递归的后半截还还有被执行。
黑色代表此节点以及其所有儿孙都已经被处理过了。
当深度遍历时,如果到达了一个灰色的节点,说明有环。
from collections import defaultdict
class Graph():
def __init__(self, V):
self.V = V
self.graph = defaultdict(list)
def addEdge(self, u, v):
self.graph[u].append(v)
def DFSUtil(self, u, color):
# GRAY : This vertex is being processed (DFS
# for this vertex has started, but not
# ended (or this vertex is in function
# call stack)
color[u] = "GRAY"
for v in self.graph[u]:
if color[v] == "GRAY":
return True#终点之一,检测到环
if color[v] == "WHITE" and self.DFSUtil(v, color) == True:
return True#递归过程
color[u] = "BLACK"
return False#终点之一,没检测到环
def isCyclic(self):
for i in range(self.V):
color = ["WHITE"] * self.V
if color[i] == "WHITE":
if self.DFSUtil(i, color) == True:
return True
return False
# Driver program to test above functions
g = Graph(5)
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 3)
g.addEdge(4, 1)
g.addEdge(2, 4)
g.addEdge(3, 4)
if(g.isCyclic()):
print ("Graph has a cycle")
else:
print ("Graph has no cycle")





 浙公网安备 33010602011771号
浙公网安备 33010602011771号