无向图检测环——Union-Find、Union By Rank and Path Compression
Union-Find
思路
给定无向图如下。
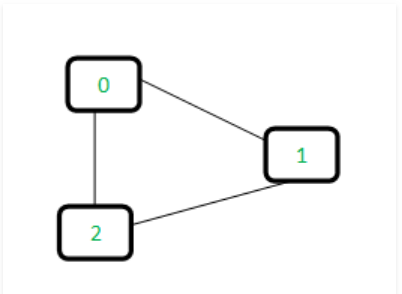
1.初始时,将无向图的n个节点作为n个子树(每个子树里面只有一个点,原文叫subset,但我觉得叫子树能更好理解),有一个n大小的parent数组,存每个节点的父节点是谁,初始时都为-1。
2.算法会遍历图中每条边,然后将该边的两个点所在的子树合并成一个新的子树。
3.合并子树时,先判断两个点的所在子树的根节点(若子树只有一个节点,则根节点就是它自己,若子树有多个节点,则一直找父亲,直到节点的父亲为-1,就找到了该子树的根节点)。
4.若两个根节点不一样,则没有检测到环,将一个根节点作为另一个根节点的父亲,这样就将两个点的所在子树合并成一个新的子树(也许你会问,到底是谁做谁的父亲呢,这里是都可以,程序要么写成第一个作第二个的父亲,或者反之)
5.若两个根节点一样即代表在同一颗子树,则检测到环,因为只有在有环的情况下,才会有一条边的两个点的所在子树是同一颗子树。
根据实际无向图分析思路:
初始时,每个节点的父节点都是-1(即代表每个节点都是一颗子树)

处理边0-1,0和1所在子树合并成一颗新子树,新子树包括0,1,根节点为1

处理边1-2,1和2所在子树合并成一颗新子树,新子树包括0,1,2,根节点为2

最后处理边0-2,发现0和2所在子树居然是同一颗子树,检测到环。
代码
代码来自geeksforgeeks,我很可耻得把代码扒下来了。
# Python Program for union-find algorithm to detect cycle in a undirected graph
# we have one egde for any two vertex i.e 1-2 is either 1-2 or 2-1 but not both
from collections import defaultdict
#This class represents a undirected graph using adjacency list representation
class Graph:
def __init__(self,vertices):
self.V= vertices #No. of vertices
self.graph = defaultdict(list) # default dictionary to store graph
# function to add an edge to graph
def addEdge(self,u,v):
self.graph[u].append(v)
# A utility function to find the subset of an element i
def find_parent(self, parent,i):#递归地寻找父亲节点,想象subset是一颗子树,直到找到根节点
if parent[i] == -1:
return i
if parent[i]!= -1:
return self.find_parent(parent,parent[i])
# A utility function to do union of two subsets
def union(self,parent,x,y):#结合两颗子树
x_set = self.find_parent(parent, x)
y_set = self.find_parent(parent, y)
parent[x_set] = y_set
# The main function to check whether a given graph
# contains cycle or not
def isCyclic(self):
# Allocate memory for creating V subsets and
# Initialize all subsets as single element sets
parent = [-1]*(self.V)
# Iterate through all edges of graph, find subset of both
# vertices of every edge, if both subsets are same, then
# there is cycle in graph.
for i in self.graph:
for j in self.graph[i]:
x = self.find_parent(parent, i)
y = self.find_parent(parent, j)
if x == y:
return True
self.union(parent,x,y)
# Create a graph given in the above diagram
g = Graph(3)
g.addEdge(0, 1)
g.addEdge(1, 2)
g.addEdge(2, 0)
#这里每条边只存一次
if g.isCyclic():
print( "Graph contains cycle")
else :#这里返回值为None,
print( "Graph does not contain cycle ")Union By Rank and Path Compression
思路
通过排名和路径压缩来结合。
讲解与代码来自geeksforgeeks。
The above union() and find() are naive and the worst case time complexity is linear. The trees created to represent subsets can be skewed and can become like a linked list. Following is an example worst case scenario.
上一个思路使用的两个方法union() and find(),最差的时间复杂度是线性,也就是O(n)。建立的子树能够被倾斜以成为一个链表。
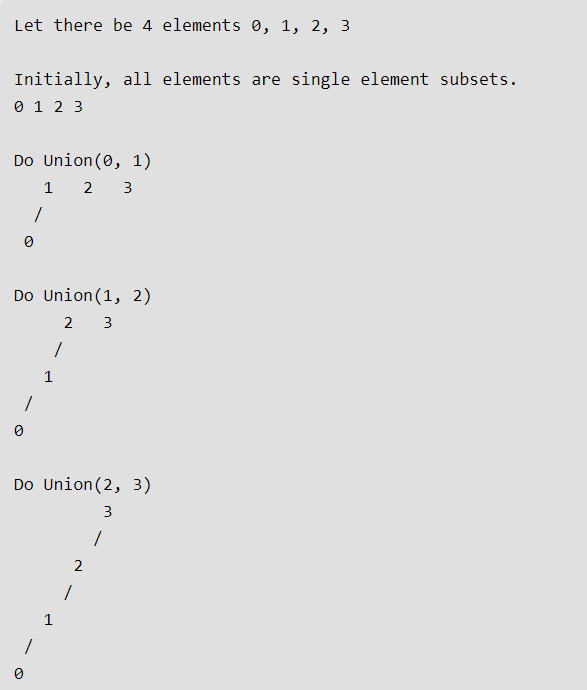
从上图可以看出,这是最差的情况。很有可能,每次寻找根节点时,都得从子树的最底下那个节点开始寻找直到根节点,这样就会造成时间复杂度为线性的。
The above operations can be optimized to O(Log n) in worst case. The idea is to always attach smaller depth tree under the root of the deeper tree. This technique is called union by rank. The term rank is preferred instead of height because if path compression technique (we have discussed it below) is used, then rank is not always equal to height. Also, size (in place of height) of trees can also be used as rank. Using size as rank also yields worst case time complexity as O(Logn) (See this for proof)
以上操作可以被优化为O(Log n)即使在最差情况。主要思想是,将更小深度的子树,给添加到更大深度的子树上去。这个技术叫union by rank。术语rank用来代替高度,是因为路径压缩技术(下面会讲到)被使用后,rank就不一定一直会等于高度的。当然,size也可以用代替高度,来当做rank的评判标准,同样能降低最差情况的时间复杂度。

如上图所示,这样构建的子树就不会像之前一样,深度特别大,而是一直保持深度为1。这样的子树来寻找根节点就会很快。
The second optimization to naive method is Path Compression. The idea is to flatten the tree when find() is called. When find() is called for an element x, root of the tree is returned. The find() operation traverses up from x to find root. The idea of path compression is to make the found root as parent of x so that we don’t have to traverse all intermediate nodes again. If x is root of a subtree, then path (to root) from all nodes under x also compresses.
第二个优化就是路径压缩。主要思想是去偏平化子树,当find方法被使用时,方法会找到当前节点x所在子树的根节点xroot,再让xroot成为x的父节点(如果已经是了就不用了),这样我们就遍历那些中间的节点了。

如上图所示,当find(3)被调用后,就将3找到的根节点9作为3新的父节点,这样就实现了路径压缩,当然,子树的深度也减小了。
The two techniques complement each other. The time complexity of each operation becomes even smaller than O(Logn). In fact, amortized time complexity effectively becomes small constant.
代码
代码来自geeksforgeeks。由于代码是C++的,由于本人没学过看着稍微有点费劲,看懂以后我给改成python的了。
原C++代码如下:
// A union by rank and path compression based program to detect cycle in a graph
#include <stdio.h>
#include <stdlib.h>
// a structure to represent an edge in the graph
struct Edge
{
int src, dest;
};
// a structure to represent a graph
struct Graph
{
// V-> Number of vertices, E-> Number of edges
int V, E;
// graph is represented as an array of edges
struct Edge* edge;
};
struct subset
{
int parent;
int rank;
};
// Creates a graph with V vertices and E edges
struct Graph* createGraph(int V, int E)
{
struct Graph* graph = (struct Graph*) malloc( sizeof(struct Graph) );
graph->V = V;
graph->E = E;
graph->edge = (struct Edge*) malloc( graph->E * sizeof( struct Edge ) );
return graph;
}
// A utility function to find set of an element i
// (uses path compression technique)
int find(struct subset subsets[], int i)
{
// find root and make root as parent of i (path compression)
if (subsets[i].parent != i)
subsets[i].parent = find(subsets, subsets[i].parent);
return subsets[i].parent;
}
// A function that does union of two sets of x and y
// (uses union by rank)
void Union(struct subset subsets[], int x, int y)
{
int xroot = find(subsets, x);
int yroot = find(subsets, y);
// Attach smaller rank tree under root of high rank tree
// (Union by Rank)
if (subsets[xroot].rank < subsets[yroot].rank)
subsets[xroot].parent = yroot;
else if (subsets[xroot].rank > subsets[yroot].rank)
subsets[yroot].parent = xroot;
// If ranks are same, then make one as root and increment
// its rank by one
else
{
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
// The main function to check whether a given graph contains cycle or not
int isCycle( struct Graph* graph )
{
int V = graph->V;
int E = graph->E;
// Allocate memory for creating V sets
struct subset *subsets =
(struct subset*) malloc( V * sizeof(struct subset) );
for (int v = 0; v < V; ++v)
{
subsets[v].parent = v;
subsets[v].rank = 0;
}
// Iterate through all edges of graph, find sets of both
// vertices of every edge, if sets are same, then there is
// cycle in graph.
for(int e = 0; e < E; ++e)
{
int x = find(subsets, graph->edge[e].src);
int y = find(subsets, graph->edge[e].dest);
if (x == y)
return 1;
Union(subsets, x, y);
}
return 0;
}
// Driver program to test above functions
int main()
{
/* Let us create the following graph
0
| \
| \
1-----2 */
int V = 3, E = 3;
struct Graph* graph = createGraph(V, E);
// add edge 0-1
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
// add edge 1-2
graph->edge[1].src = 1;
graph->edge[1].dest = 2;
// add edge 0-2
graph->edge[2].src = 0;
graph->edge[2].dest = 2;
if (isCycle(graph))
printf( "Graph contains cycle" );
else
printf( "Graph doesn't contain cycle" );
return 0;
}看完以后我发现一个问题,就是,明明说好了有路径压缩的,但是程序却没有体现出来。在函数Union中,当xroot和yroot被找到后,应该有以下操作的:
if(xroot != subsets[x].parent)
{
subsets[x].parent = xroot
}
if(yroot != subsets[y].parent)
{
subsets[y].parent = yroot
}本人写的python的代码,给定无向图如下:
from collections import defaultdict
class subset:
def __init__(self,i):
self.parent = i
self.rank = 0
def __repr__(self):#方便打印看具体的值
return 'parent'+str(self.parent)+'rank'+str(self.rank)
class Graph:
def __init__(self,vertices):
self.V= vertices
self.graph = defaultdict(list)
def addEdge(self,u,v):
self.graph[u].append(v)
def find_parent(self, subsets,i):#递归地寻找父亲节点,想象subset是一颗子树
if subsets[i].parent == i:#这里返回根节点的条件是,等于自身
return i
if subsets[i].parent != i:
return self.find_parent(subsets,subsets[i].parent)
def union(self,subsets,x,y):#根据rank结合两颗子树
xroot = self.find_parent(subsets, x)
yroot = self.find_parent(subsets, y)
#进行路径压缩
if(xroot != subsets[x].parent):
subsets[x].parent = xroot
if(yroot != subsets[y].parent):
subsets[y].parent = yroot
if(subsets[xroot].rank < subsets[yroot].rank):
subsets[xroot].parent = yroot
elif(subsets[xroot].rank > subsets[yroot].rank):
subsets[yroot].parent = xroot
else:
subsets[yroot].parent = xroot
subsets[xroot].rank += 1
def isCyclic(self):
subsets = []
for i in range(self.V):
subsets.append(subset(i))
for i in self.graph:
for j in self.graph[i]:
x = self.find_parent(subsets, i)
y = self.find_parent(subsets, j)
print(subsets)
if x == y:
return True
self.union(subsets,x,y)
g = Graph(5)
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 3)
g.addEdge(4, 1)
g.addEdge(3, 4)
#这里每条边只存一次
if g.isCyclic():
print( "Graph contains cycle")
else :#这里返回值为None,
print( "Graph does not contain cycle ")
程序分析:
find方法判定根节点的标准,变成是否为自身,之前为是否为-1,都一样。
只有在两颗子树的rank相同时才会增加rank。
增加rank只给子树的根节点增加,也就是说,看子树除根节点以外的点的rank是没有意义的。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号