归并排序 改进归并

归并排序

归并排序的主要思想是：分治（divide-and-conquer）策略，首先是分，先把问题拆分成规模很小的问题；然后是治，将子问题的答案合并成一个更大的小问题的答案，直到合并成问题本身的答案。

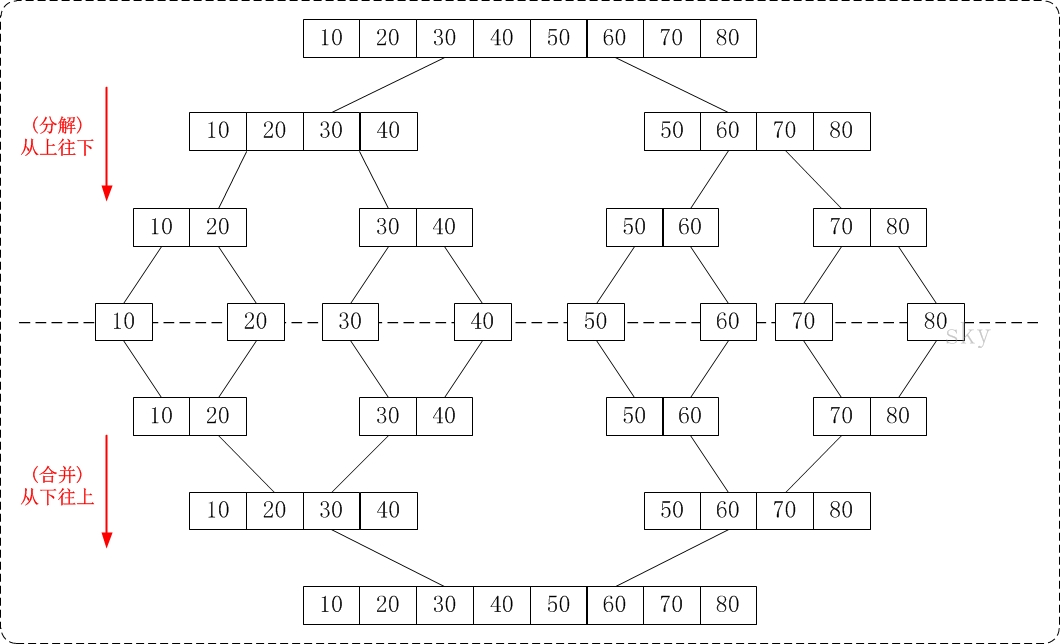
分解的过程就是一颗二叉树，既然是二叉树，递归深度也就知道了是$\log_2n$。

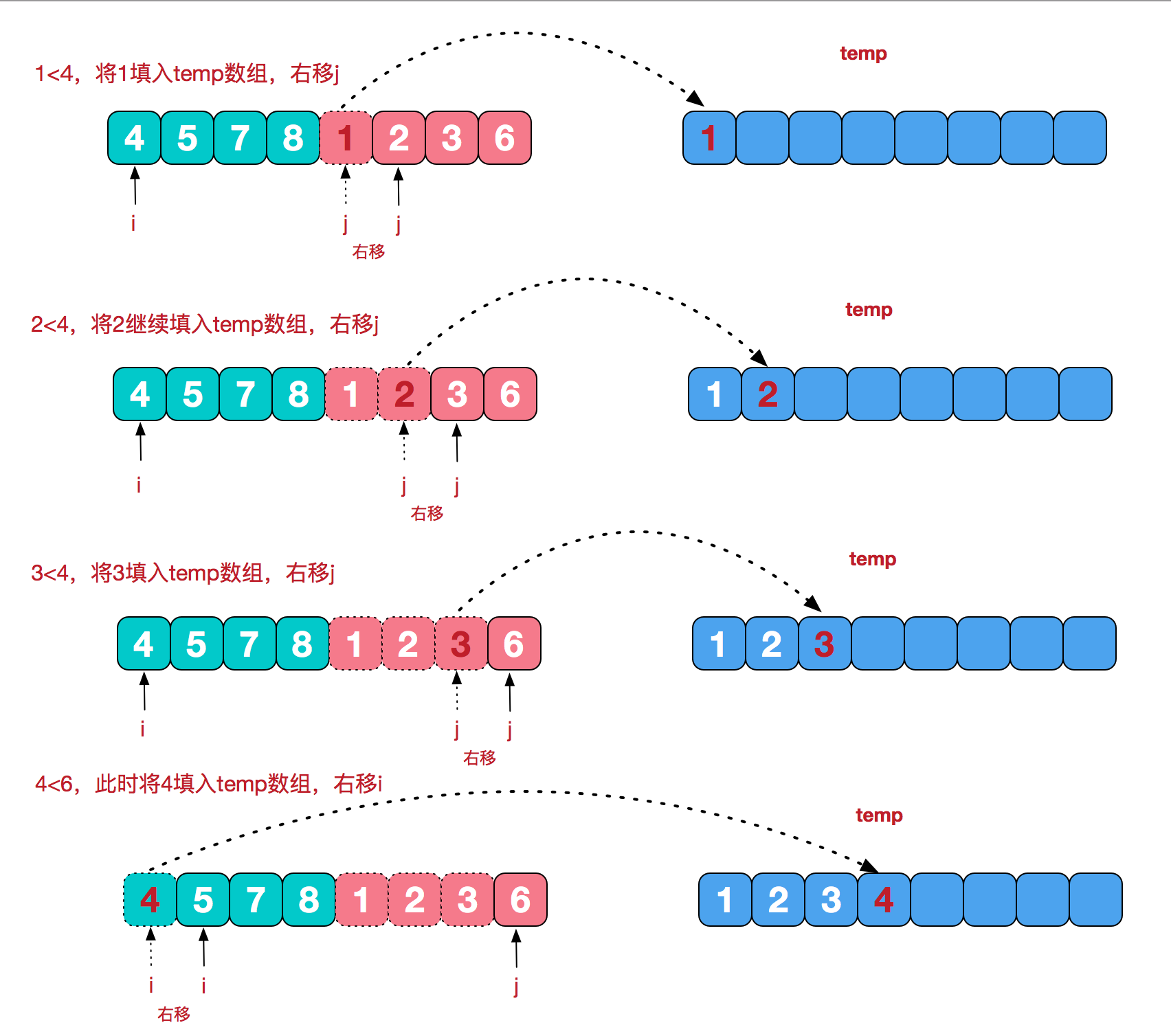
再来看合并的过程，分别会有两个指针指向两个子序列的开头。还会有一个副本数组暂存数据。有两种情况：
1）如果两个指针指向的元素都是子序列中的元素，那么比较两个元素，将较小元素放入副本数组，后移对应指针。
2）如果只有一个指针指向的元素还是子序列中的元素，那么就将指针指向元素放入副本数组，后移对应指针。

def merge(start,former,latter,end,src,des):
    #分治策略的治
    gap = end -start +1
    i = start
    j = latter
    for step in range(gap):
        if (i<=former) and (j<=end):#两个子序列都没复制完，得判断大小
            if src[i] <= src[j]:# =保证算法稳定
                des[start+step] = src[i]#把前子序列元素复制到副本数组
                i += 1#指针后移
            else:
                des[start+step] = src[j]#把后子序列元素复制到副本数组
                j += 1#指针后移
        elif (i<=former):#前子序列还没复制完
            des[start+step] = src[i]
            i += 1
        elif (j<=end):#后子序列还没复制完
            des[start+step] = src[j]
            j += 1
    #最后一个循环必须有，因为每次治的时候都是以src的两个子序列有序为前提
    #des只是暂时放一下，因为归并排序性质所以必须有一个副本存在
    for step in range(gap):
        src[start+step] = des[start+step]

def merge_sort(start,end,src,des):
    #分治策略的分，既然是分，只需要start end，再看二者距离看可以分不
    #如果可以分，就分开；不然就是递归终点
    if start < end:
        mid = (start+end)//2
        merge_sort(start,mid,src,des)
        merge_sort(mid+1,end,src,des)
        merge(start,mid,mid+1,end,src,des)
    #当start>=end，递归终点，是一个空壳函数，然后两个空壳函数返回上一层
    #执行上一层函数的最后一句merge，是对两个长度为1的有序序列进行合并

def copy_array(arr):
    return [None for i in range(len(arr))]

arr = [9,8,4,5,7,1,3,6,2]
temp = copy_array(arr)#数组副本
n = len(arr)

merge_sort(0,n-1,arr,temp)
print(arr)

重要的话都写到注释里了。再提一下：
1）merge_sort函数代表“分”操作，是递归实现，递归终点是一个空壳函数。因为是递归，所以是到了终点才能开始返回，所以就能实现将问题分解成最小规模的子问题后才开始合并子问题的答案。

改进归并排序

会有两种特殊情况，明显需要特殊处理：
1）前子序列的最大值<=后子序列的最小值,直接返回
2）后子序列的最大值<=前子序列的最小值，虽然不能直接返回，但也需要特殊处理。就是先复制后子序列，再复制前子序列。

def merge(start,former,latter,end,src,des):
    gap = end -start +1
    i = start
    j = latter
    if src[former] <= src[latter]:
        #前子序列的最大值<=后子序列的最小值,直接返回
        #print('第一种情况')
        return
    elif src[end] <= src[start]:
        #后子序列的最大值<=前子序列的最小值，也需要特殊处理
        #print('第二种情况')
        for step in range(gap):
            if j<=end:
                des[start+step] = src[j]
                j += 1
            elif i<=former:
                des[start+step] = src[i]
                i += 1
    else:
        #正常的归并操作
        for step in range(gap):
            if (i<=former) and (j<=end):
                if src[i] <= src[j]:# =保证算法稳定
                    des[start+step] = src[i]
                    i += 1
                else:
                    des[start+step] = src[j]
                    j += 1
            elif (i<=former):
                des[start+step] = src[i]
                i += 1
            elif (j<=end):
                des[start+step] = src[j]
                j += 1
    for step in range(gap):
        src[start+step] = des[start+step]

def merge_sort(start,end,src,des):
    if start < end:
        mid = (start+end)//2
        merge_sort(start,mid,src,des)
        merge_sort(mid+1,end,src,des)
        merge(start,mid,mid+1,end,src,des)


def copy_array(arr):
    return [None for i in range(len(arr))]

arr = [1,2,3,4,7,8,5,6]
result = copy_array(arr)
n = len(arr)

merge_sort(0,n-1,arr,result)
print(arr)