逆序数问题 使用归并排序

在一个排列中，如果一对数的前后位置与大小顺序相反，即前面的数大于后面的数，那么它们就称为一个逆序。一个排列中逆序的总数就称为这个排列的逆序数。
比如3 4 1 2这个数组有4对逆序：分别是[3,1] [4,1] [3,2] [4,2]。
本文使用归并排序来求逆序数。

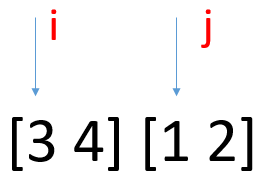
假设归并排序已经进行到了如上这个状态，正要把两个长度为2的有序子序列，合并成一个长度4的有序序列。
i指向前子序列。j指向后子序列。很明显，当j指向元素小于i指向元素时，就肯定是产生了逆序对了。而逆序对的个数则与i指向元素在前子序列中的位置有关，是从i开始到前子序列的最后元素的个数（包括i和最后元素来统计），通俗地讲，就是如果j比i小，那么j肯定也比i之后的元素还小（当然这里是指在前子序列中的范围）。
如上图，1比3小，那么1必然也比3后面的元素4小。

def merge(start,former,latter,end,src,des):
    gap = end -start +1
    i = start
    j = latter
    count = 0
    for step in range(gap):
        if (i<=former) and (j<=end):
            if src[i] <= src[j]:
                des[start+step] = src[i]
                i += 1
            else:#只有进入else才代表有逆序对
            	#j元素比i元素小，那么j肯定也比前子序列中的i后面的元素小
                des[start+step] = src[j]
                j += 1
                count += latter - i#记录下来前子序列i之后元素个数，包括i
        elif (i<=former):
            des[start+step] = src[i]
            i += 1
        elif (j<=end):
            des[start+step] = src[j]
            j += 1
    for step in range(gap):
        src[start+step] = des[start+step]
    return count

def merge_sort(start,end,src,des):

    if start < end:
        count = 0
        mid = (start+end)//2
        count += merge_sort(start,mid,src,des)#加上左子序列的逆序对数
        count += merge_sort(mid+1,end,src,des)#加上右子序列的逆序对数
        count += merge(start,mid,mid+1,end,src,des)#再加上左右子序列合并时，发现的逆序对数
        return count
    return 0#递归终点返回0

def copy_array(arr):
    return [None for i in range(len(arr))]

arr = [9,8,4,5,7,1,3,6,2]
temp = copy_array(arr)
n = len(arr)

num = merge_sort(0,n-1,arr,temp)
#print(arr)
print(num)

代码改自本人另一篇博客归并排序 改进归并，其中的基本归并排序的代码。