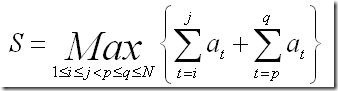【原】 POJ 2593 Max Sequence 动态规划 解题报告

 

http://poj.org/problem?id=2593

 

Maximum Sequence
求数组两段不重叠的连续子数组的最大和
详见2479

 

Description

Give you N integers a1, a2 ... aN (|ai| <=1000, 1 <= i <= N).

You should output S.

Input

The input will consist of several test cases. For each test case, one integer N (2 <= N <= 100000) is given in the first line. Second line contains N integers. The input is terminated by a single line with N = 0.

Output

For each test of the input, print a line containing S.

Sample Input

5

-5 9 -5 11 20

0

Sample Output

40

 

#include <stdio.h>
#include <iostream>

using namespace std ;


const int N = 100000 ;

int a[N] ;
int maxsofar[2][N] ;

void run2593()
{
    int n,val ;
    int i,j ;
    int maxendinghere ;
    int max ;
    int sum ;

    while(  scanf( "%d", &n ) && n!=0 )
    {
        scanf( "%d", &a[0] ) ;
        maxendinghere = a[0] ;
        maxsofar[0][0] = a[0] ;
        for( i=1 ; i<n ; ++i )
        {
            scanf( "%d", &a[i] ) ;
            maxendinghere = std::max( a[i] , maxendinghere+a[i] ) ;
            maxsofar[0][i] = std::max( maxsofar[0][i-1] , maxendinghere ) ;
        }

        maxendinghere = a[n-1] ;
        maxsofar[1][n-1] = a[n-1] ;
        max = maxsofar[0][n-2] + a[n-1] ;
        for( i=n-2 ; i>0 ; --i )
        {
            maxendinghere = std::max( a[i] , a[i]+maxendinghere ) ;
            maxsofar[1][i] = std::max( maxsofar[1][i+1] , maxendinghere ) ;
            sum = maxsofar[0][i-1] + maxsofar[1][i] ;
            max = max>sum ? max : sum ;
        }
        printf( "%d\n" , max ) ;
    }
}