蒙特卡洛方法试验的一般过程和经典例子

本文首发于：算法社区，转发请注明出处。

前言

蒙特卡洛方法是基于概率统计为基础的近似解求解方法，它是通过大量试验来使近似解逼近准确解，而大量的试验又是基于大数极限理论，试验越多，其解越精确，误差也就越小。下面分别讲述蒙特卡洛试验的解题步骤、实际使用中需要的注意点，最后给出一个最经典的例子（求 \(\pi\) 值）作为本文的结束点。

蒙特卡洛方法（或试验）解题的步骤

1. 人为构造或描述问题的概率过程
2. 从已知概率分布中进行抽样（随机变量抽样）
3. 求各统计量的估计
4. 使用统计量的估计最终求近似解

在实际使用中需要的注意点

• 要列出所求问题相关的变量
• 把变量进行分类：随机变量和非随机变量，非随机变量又分为自变量和因变量
• 随机变量涉及了概率分布
• 通过随机变量和非随机变量构造所要求解的统计量
• 通过随机变量的抽样求统计量的估计值
• 使用估计值来替代统计量，从而求得问题的近似解
• 说明：蒙特卡洛方法中，必有随机变量和概率

实例（最经典pi值求解过程-浦丰氏问题）

在十九世纪后期，曾有很多人以任意投掷一根针到地面上，将针与地面上两条平行线相交的频率作为与该
两条平行线相交概率的近似值，然后根据这一概率的理论值求出圆周率 pi 的近似值。

说明：这里的相交不是延长线的相交，而是针与平行线接触，有交点。

首先我们来正确的描述和模拟这个问题

这里我借用了文献上的图片：

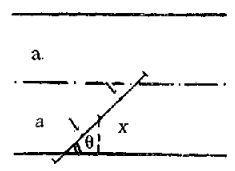
变量说明：\(2a\) 表示两条平行线的距离，图中虚线是在两平行线的中间，即 \(a\) 的位置, \(2l\) 是这根针的长度， \(l\) 是这个针的半长，\(x\) 表示针中心位置到平行线的 y 轴坐标值，\(\theta\) 是针与平行线交叉角度

从图中所示，我们可以知道，平面上针的位置是由针中心的坐标位置 和 针与平行线的夹角 \(\theta\) 决定的。任意投针，意味着 \(x\) 和 \(\theta\) 都是任意的（它们是随机变量）。\(\theta\)的范围为 \(\left [ 0, \pi \right ]\)，\(x\) 的范围为\(\left [ 0, a \right ]\)。

此时相交的条件为：

\(x\le l\sin \theta,0\le x\le a,0\le \theta \le \pi\)

随机变量 \(x\) 和 \(\theta\) 取值的随意性，说明它们是随机数，是在范围内的随机数，所以它们的分布密度分别为：

\[\begin{align} f_1\left ( x \right ) & = \begin{cases} \frac{1}{a},0\le x\le a \\ 0,其他, \end{cases} \notag\\ f_2\left ( \theta \right ) & = \begin{cases} \frac{1}{\pi },0\le \theta\le \pi \\ 0,其他. \end{cases} \notag \end{align}\]

细心的读者可能已经发现， \(x\) 和 \(\theta\) 是相互独立的，并且都是服从各自区间上的均匀分布的随机变量。所以这二维随机变量的概率密度为

\[f\left ( x,\theta \right ) =f_1\left ( x \right ) f_2\left ( \theta \right ) \]

最后定义一个综合随机变量（用于计算概率的）

\[s\left ( x_i,\theta_i \right ) =\begin{cases} 1,x_i\le l\sin \theta_i \\ 0,其他 \end{cases}\]

意思是相交则为 1，否则为 0

开始抽样和求估计值

如果投掷 N 次，那么相交的频率为

\[\bar{s}_N=\frac{1}{N}\sum_{i=1}^{N} s\left ( x_i,\theta_i \right ) \]

是相交概率的估计值。

而根据二维随机变量的概率计算公式来求相交概率是

\[p=\iint s\left ( x,\theta \right ) f\left ( x,\theta \right ) dxd\theta =\int_{0}^{\pi } \frac{1}{\pi} d\theta\int_{0}^{l\sin \theta }\frac{1}{a}dx=\frac{2l}{a\pi} \]

通过估计值求解的近似值

于是就有

\[\pi=\frac{2l}{ap} \approx \frac{2l}{a\bar{s}_N } \]

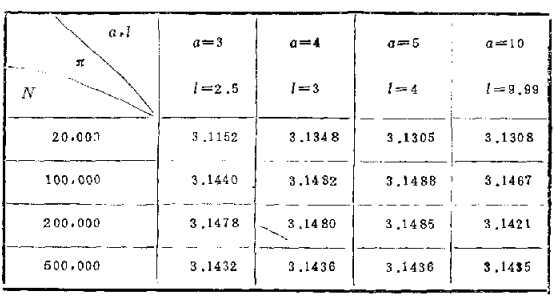
计算机模拟计算的结果

结论

蒙特卡洛试验的本质是用概率过程来描述问题，并且使得概率（或某个统计量）是这个解的某个参数，最后通过概率或统计量的估计值来计算这个解的近似值。最好的方式就是概率或统计量本身就是解的值。根据上述过程，我们注意到：用正确的概率模型来描述问题非常重要（就是用概率方式来描述），其次，分清随机变量其及服从的分布也是至关重要的一步，基本的关键点就是这些了。