[配翻译]A Fixed-Point Introduction by Example
本文首发于 dspstack.com,转载请注明出处,谢谢。
作者:Christopher Felton,翻译:ALLEN
翻译感想
翻译一篇文章,不仅需要专业上的知识,更需要的是耐心,和琢磨作者原文的真正含义,以负责任的态度对待每一篇文章,因为心里想着如何能让读者获取到正确的知识
翻译如有不当,还请大家指正
Introduction(介绍)
The finite-word representation of fractional numbers is known as fixed-point. Fixed-point is an interpretation of a 2's compliment number usually signed but not limited to sign representation. It extends our finite-word length from a finite set of integers to a finite set of rational real numbers [1]. A fixed-point representation of a number consists of integer and fractional components. The bit length is defined as:
译:分数的有限字长的表示称为定点。定点数是 2 的补码的一种解释,补码通常是有符号的但不限于有符号的表示。定点数把有限字长从整数的有限集合拓展到有理实数的有限集合[1]。数字的定点表示由整数部分和小数部分组成。其位长定义为:
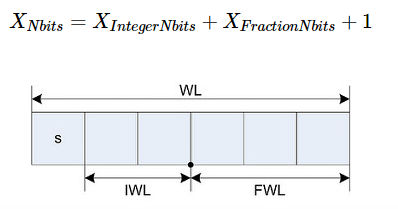
IWL is the integer word length, FWL is the fractional word length, and WL is the word length. For 2's compliment fixed-point representation WL = 1 + IWL + FWL.With this representation the range of the number is \([-2^{IWL},2^{IWL})\) and a step size (resolution) of \(2^{-FWL}\) [2]. The fixed-point number is defined by its format wl, iwl, fwl or its properties range, resolution, and bias.
译:IWL 是整数部分的字长,FWL 是小数部分的字长,以及 WL 是整个字长。对于2的补码定点表示则有:WL = 1 + IWL + FWL。所以该数的区间为 \([-2^{IWL},2^{IWL})\) 并且其步长(分辨率)为 \(2^{-FWL}\) [2]。定点数由它的格式:字长,整数部分字长和小数部分字长 或 它的属性:值区间,分辨率 和 误差 定义。
As described, a fixed-point number is defined by its range and resolution, instead of the number of bits. When designing a fixed-point system it is logical to use range and resolution requirements and algorithmically resolve the number of bits when it comes time to implement the design. In other words, start with range and resolution when designing / specifying and move to the number of bits required when implementing.
译:正如之前所讲,定点数由它的区间和分辨率定义,而不是数的位数。所以在设计一个定点系统时,当需要实现这个设计时使用区间和分辨率作为必要条件并且从算法上解决数的位数的这种做法是合理的。换言之,设计 / 约束条件 以区间和分辨率入手,实现设计时再转到需要的数的位数上。
Typically, a short hand is used to represent the format. The Q-format is common when discussing fixed-point processors. I will not use the Q-format because it is not as flexible and can be confusing with the notation used in older fixed-point processor documents [3]. Here I will use an explicit notation, W=(wl,iwl,fwl). This notation defines the number of integer bits, fraction bits, and the total bit length. Example, W=(4,0,3) is a 4-bit number with three fractional bits and a sign bit (the sign bit is implicit). All fixed-point numbers in this post will be 2's complement representation (sign bit is always present).
译:典型地,用速记方式来表示数的格式。当讨论定点处理器时,Q-格式是普遍使用的。但我不会使用Q-格式,因为这种格式不够灵活并且会与在旧的定点处理器说明书上使用的记号相混淆[3]。这里,我会使用一个显式记号,W=(wl,iwl,fwl)。这个记号定义了整数bit位数,小数bit位数和整个数的bit位数。比如,W=(4,0,3) 是一个3个小数bit位和一个符号位(符号位是隐含的)的4-bit位的数字。本文的所有定点数都是2的补码表示(即符号位一直存在的)。
WHY USE FIXED-POINT(为什么要使用定点)
Why use fixed-point representation? Why not simply normalize all values to an integer range and deal with integers. Depending on your point of view this might be obvious or not. I have found many designers prefer to normalize all values to integers but this produces very unreadable code and documentation. Fixed-point is normally used for convenience (similar to the use of exp(jω) ). Example, if I am looking at source code and I see:
译:为什么要使用定点表示?为什么不直接把所有值标准化到一个整数区间然后来处理整数。取决于你的观点,这可能是显而易见的,或者不是。我发现许多设计师更喜欢把所有值标准化到整数,但是这样产生了相当程度上无法阅读的代码和文档。通常定点使用是为了方便(类似于指数 exp(jw) 的使用)。比如,如果我正在看代码并且看到:
c0 = fixbv(0.0032, min=-1, max=1, res=2**-15)
c1 = fixbv(-0.012, min=-1, max=1, res=2**-15)
I can easily relate this back to the coefficients of a filter but if I see the integer use only:
译:我可以很容易地把这些代码关联到一个滤波器的系数,但是如果我看到只使用整数的代码:
c0 = intbv(0x0069, min=-2**15, max=2**15)
c1 = intbv(-0x0189, min=-2**15, max=2**15)
additional information (documentation) is required. The integer only is difficult to understand what the values are intended to represent. In addition to the representation benefits, tools to handled rounding and overflow are common with fixed-point types.
译:额外的信息(文档)是必需的。只有整数很难理解这些值试图表达的含义。除了表达带来的好处,处理取舍和溢出的工具带有定点类型也是普遍的。
Now that we have given the basic definition of a fixed-point binary word and given a couple reasons why fixed-point might be used. Let's take a look at some fractional values converted to a fixed-point type. Table 1 is an example of
fixed-point representations.
译:现在我们已经给出了定点二进制字的基本定义并且给出了一些为什么定点需要使用的理由。让我们来看看一些转成定点的小数值。表1 是定点表示的一个例子。
表1
二进制 十六进制 十进制 浮点小数 定点小数 实际值 0100000000000000 4000 16384 0.50000000 0.50000000 1/2 0010000000000000 2000 8192 0.25000000 0.25000000 1/4 0001000000000000 1000 4096 0.12500000 0.12500000 1/8 0000100000000000 0800 2048 0.06250000 0.06250000 1/16 0000010000000000 0400 1024 0.03125000 0.03125000 1/32 0000001000000000 0200 512 0.01562500 0.01562500 1/64 0000000100000000 0100 256 0.00781250 0.00781250 1/128 0000000010000000 0080 128 0.00390625 0.00390625 1/256 0000000001000000 0040 64 0.00195312 0.00195312 1/512 0000000000100000 0020 32 0.00097656 0.00097656 1/1024 0000000000010000 0010 16 0.00048828 0.00048828 1/2048 0000000000001000 0008 8 0.00024414 0.00024414 1/4096 0000000000000100 0004 4 0.00012207 0.00012207 1/8192 0000000000000010 0002 2 0.00006104 0.00006104 1/16384 0000000000000001 0001 1 0.00003052 0.00003052 1/32768 0010101010101011 2AAB 10923 0.33333000 0.33334351 0.33333 0101101001111111 5A7F 23167 0.70700000 0.70700073 0.707 0000000000001010 000A 10 0.0003141592 0.00030518 0.0003141592 0000000000000011 0003 3 0.000086476908 0.00009155 0.000086476908
b7 b6 b5 b4 b3 b2 b1 b0
S F F F F F F F
0 1 0 1 1 0 0 1
+-1 1/2 1/4 1/8 1/16 1/32 1/64 1/128
Value = + 1/2 + 1/8 + 1/16 + 1/128 which equals
= + 0.5 + 0.125 + 0.0625 + 0.0078125
= 0.6953125
The previous two examples illustrate how to represent a fractional value using fixed-point nomenclature. In general the value of the binary word is the following if the integer and fractional parts are treated as separate bit-vectors (i.e. don't share a bit index):
译:前面的两个例子说明了怎样使用术语定点来表示一个小数值。一般地,如果整数部分和小数部分使用独立的bit向量(即不共用一个bit位下标),那么二进制字的值为如下:
\(\sum_{k=0}^{IWL-1}b_I[k]2^k+\sum_{k=0}^{FWL-1}b_F[k]2^{-(k+1)}\)
In the above equations, it assumes the bit magnitude increases with the bit index. If visualized the fractional word would be flipped relative to the depiction above.
译:在上述方程中,假设位大小随着位下标增加而增加。如果对字结构可视化,小数字相对于上述的描述要翻转过来。
Multiplication and Addition Examples(乘法和加法例子)
The following are fixed-point examples for multiplication and addition. Fixed-point subtraction can be calculated in a similar manner to a 2's complement subtraction (addition with a negative). The difference being the "point" bookkeeping required which is the same as addition. For addition and subtraction the points need to be aligned before the operation (bookkeeping). The "point" bookkeeping is usually calculated at design time and not run time (I say usually because there is the idea of block fixed-point but that is beyond the scope of this post).
译:接下来是定点数的乘法和加法例子。定点数的减法可以以类似于2的补码相减(和一个负数相加)的方式操作。不同之处在于和加法一样的“点”记。对于加法和减法,这些点在操作(记录)之前需要对齐。“点”记经常在设计阶段计算而不是在运行阶段(我说经常因为存在块定点的思想,但是这个已经超出了本文的范围)。
MULTIPLICATION(乘法)
Fixed-point multiplication is the same as 2's compliment multiplication but requires the position of the "point" to be determined after the multiplication to interpret the correct result. The determination of the "point's" position is a design task. The actual implementation does not know (or care) where the "point" is located. This is true because the fixed-point multiplication is exactly the same as a 2's complemented multiplication, no special hardware is required.
译:定点乘法与2的补码乘法是一样的,但是乘法之后需要确定“点”的位置来获得正确的计算结果。“点”的位置的确定是一个设计任务。实际实现不需要知道(或者关心)“点”位于哪里。确实如此,因为定点数相乘正好与2的补码乘法是一致的,不需要特殊的硬件。
The following is an example and illustrates 6.5625(W=(8,3,4))∗4.25(W=(8,5,2))
译:下面是一个例子并且展示了 6.5625 ( W = (8, 3, 4) ) ∗ 4.25 ( W = (8, 5 ,2 ) )
0110.1001 == 6.5625
000100.01 == 4.25
01101001
x 00010001
------------
01101001
00000000
00000000
00000000
01101001
00000000
00000000
00000000
--------------------
x000011011111001 == 0000011011.111001 == 27.890625
The number of bits required for the product (result) is the multiplicand's WL + the multiplier's WL (WLmultiplicand+WLmultiplier). It is typical for the results of multiplication (and addition) to be resized and the number of bits reduced. In fixed-point this makes intuitive sense because the smaller fractional bits are discarded and the value is rounded based on the discarded bits. Additional hardware is commonly included to perform the rounding task and reduce the number of bits to a reasonable data-path bus width.
译:乘积(结果)需要的比特位数是被乘数的 WL + 乘数的 WL (WLmultiplicand + WLmultiplier)。对乘法(和加法)的结果调整大小是典型做法,并且比特位数被缩减。在定点数中这个是有道理的,因为较小的小数位被舍弃并且这个值是基于舍弃之后的比特位数进行四舍五入的。额外的硬件通常包含进来来执行四舍五入的任务并将比特位数缩减到一个合理的数据路径总线宽度。
ADDITION(加法)
Addition is a little more complicated because the points need to be aligned before performing the addition. Using the same numbers from the multiplication problem:
译:加法稍微复杂点,因为这些点需要在相加之前对齐。使用乘法例子的相同数字:
0110.1001 == 6.5625
000100.01 == 4.25
0110.1001
+ 000100.01
-------------
001010.1101 == 10.8125
When adding (subtracting) two numbers an additional bit is required for the result. When adding more than two numbers all of the same WL width, the number of bits required for the result is WL+log2(N) where N is the number of elements being summed.
译:当对两个数字进行相加(相减)时,其结果需要额外的比特位的。当对多于两个相同 WL 宽度的数进行相加时,其结果需要的比特位个数是 WL+log2(N) ,其中 N 是被相加元素的个数。
0110.1001 == 6.5625
000100.01 == 4.25
0110.1001
+ 000100.01
-------------
001010.1101 == 10.8125
小结
Fixed-point representation is convienent and useful when dealing with signal processing implementations. This post is a basic introduction to fixed-point numbers. For a more comprehensive coverage of the subject see the references for more information.
译:当处理信号处理实现时,定点表示是方便和有用的。本文是对定点数的基本介绍。对于这个主题更广泛的覆盖可参考引用文献来获得更多的信息
[1]: Yates, Randy, "Fixed-Point Arithmetic: An Introduction"
[2]: K.B. Cullen, G.C.M. Silvestre, and .J. Hurley, "Simulation Tools for Fixed Point DSP Algorithms and Architectures"
[3]: Texas Instruments Example
[4]: Ercegovac, Milos Lang, Thomas, "Digital Arithmetic"
[5]: Kuo, Lee, Tian, "Real-Time Digital Signal Processing"



