本文首发于 算法社区, 转载请注明出处，谢谢。
写在前面
统计学是个好东东，说它是个好东东，因为统计学不像其他有些学科，它不仅在科研领域应用广泛，在平常的生活中我们也会经常碰到。当然我们要研究的主要还是在科研领域的应用。
本文讲讲经典的隐含马尔可夫模型，同时说明本文所讲的马尔可夫模型所用的记号都偏向于信号处理的。
隐含马尔可夫模型
隐含马尔可夫模型（HMM）是一个二元变量离散时间过程 \(\left ( X_{n},Y_{n} \right )\)，其中 \(X_{n}\) 和 \(Y_{n}\) 是两个有限维数的实数随机向量，分别定义如下：
\(X_{n},n\ge 0\)，是一个马尔可夫随机过程，即对于任意函数 \(f\) ，由 \(\left \{ X_{s};s\le n \right \}\)（过去直到 \(n\) 的值）产生的\(f\left ( X_{n+1} \right )\)条件期望 \(\sigma\) 等于由\(\left \{ X_{n} \right \}\)产生的 \(f\left ( X_{n+1} \right )\) 条件期望 \(\sigma\)。如果条件概率分布具有概率密度，则可被写为：
\[p_{X_{n+1}|X_{0:n}}\left ( x_{n+1};x_{0:n} \right ) = p_{X_{n+1}|X_{n}}\left ( x_{n+1};x_{n} \right ) （3-1）
\]
\(Y_{n},n\ge 0\)，是一个随机过程，给定 \(X_{0},...,X_{n-1}\) 的 \(Y_{0},...,Y_{n-1}\) 条件概率分布是条件 \(X_{k}\) 的 \(Y_{k}\) 概率分布的乘积。如果条件概率分布具有概率密度，则可被写为：
\[p_{Y_{0:n}|X_{0:n}}\left ( y_{0:n};x_{0:n} \right ) = \prod_{k=0}^{n} p_{Y_{k}|X_{k}}\left ( y_{k};x_{k} \right ) （3-2）
\]
初始的实数随机向量 \(X_{0}\) 具有已知概率分布律。如果这个初始概率分布具有概率密度，那么它会被记为 \(p_{X_{0}}\left ( x_{0} \right )\) 。
接下来联合概率分布的表达式可以因为之前的假设被缩减为：
\[p_{X_{0:n},Y_{0:n}}\left ( x_{0:n},y_{0:n} \right ) = \prod_{k=0}^{n} p_{Y_{k}|X_{k}}\left ( y_{k};x_{k} \right ) \prod_{k=1}^{n} p_{X_{k}|X_{k-1}}\left ( x_{k};x_{k-1} \right ) p_{X_{0}}\left ( x_{0} \right ) （3-3）
\]
对于式（3-3），我们做些证明：
使用贝叶斯公式和式（3-2），我们有：
\[p_{X_{0:n},Y_{0:n}}\left ( x_{0:n},y_{0:n} \right ) = p_{Y_{0:n}|X_{0:n}}\left ( y_{0:n},x_{0:n} \right ) p_{X_{0:n}}\left ( x_{0:n} \right ) \\
=\prod_{k = 0}^{n} p_{Y_{k}|X_{k}}\left ( y_{k};x_{k} \right ) p_{X_{0:n}}\left ( x_{0:n} \right )
（3-3-1）\]
再使用贝叶斯公式和式（3-1），我们可以写为：
\[\begin{align}
p_{X_{0:n}}\left ( x_{0:n} \right ) & = p_{X_{n}|X_{0:n-1}}\left ( x_{n};x_{0:n-1} \right ) p_{X_{0:n-1}}\left ( x_{0:n-1} \right ) \notag\\
&=p_{X_{n}|X_{n-1}}\left ( x_{n};x_{n-1} \right ) p_{X_{0:n-1}}\left ( x_{0:n-1} \right ) \notag
\end{align}\]
重复这个过程，我们就有：
\[p_{X_{0:n}}\left ( x_{0:n} \right ) = \prod_{k=1}^{n} p_{X_{k}|X_{k-1}}\left ( x_{k};x_{k-1} \right ) p_{X_{0}}\left ( x_{0} \right ) （3-3-2）
\]
把式（3-3-2）代入式（3-3-1）即得证。
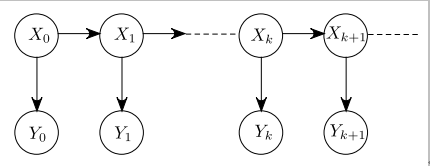
式（3-3）也许可通过有向非循环图（directed acyclic graph, DAG）来表示，如图3.1所示。
图 3.1 HMM的有向非循环图（DAG）
使用编码规则表示：
\[P\left \{ X_{0:n},Y_{0:n} \right \} = \prod_{i\in \upsilon }^{} P\left \{ i|parent\left ( i \right ) \right \}
\]
其中 \(\upsilon\) 表示图中所有节点的集合。注意到一个 HMM 的 DAG 是一棵树。在更一般的例子中，我们会谈到动态贝叶斯网络。
实际应用说明
在实际应用中，变量 \(Y_{0:n}\) 代表观测值和变量 \(X_{0:n}\) 代表“隐含”变量。我们的目标是基于观测值对隐含变量做出推测。在更一般用语中，我们因此需要计算形如 \(p_{X_{n_{1}:n_{2}}|Y_{m_{1}:m_{2}}}\left ( x_{n_{1}:n_{2}};y_{m_{1}:m_{2}} \right )\) 的条件概率密度。因此，如果我们希望“抽取”关于基于观测值 \(Y_{0:n}\) 的 \(X_{n}\) 的所有信息，我们需要确定概率密度$p_{X_{n}|Y_{0:n}} \left ( x_{n};y_{0:n} \right ) $。接着，任意函数 \(f\left ( X_{n} \right )\) 可使用条件期望来计算：
\[E\left \{ f\left ( X_{n} \right )|Y_{0:n} \right \} =\int f\left ( x \right ) p_{X_{n}|Y_{0:n}}\left ( x;Y_{0:n} \right ) dx
\]
它是一个观测值的“可测量的”函数。
有这个先验知识，这个问题就变得简单了。我们只是需要应用贝叶斯公式并且可以写为：
\[p_{X_{n_{1}:n_{2}}|Y_{m_{1}:m_{2}}}\left ( x_{n_{1}:n_{2}};y_{m_{1}:m_{2}} \right ) =\frac{p_{X_{n_{1}:n_{2}},Y_{m_{1}:m_{2}}}\left ( x_{n_{1}:n_{2}},y_{m_{1}:m_{2}} \right ) }{p_{Y_{m_{1}:m_{2}}}\left ( y_{m_{1}:m_{2}} \right )}
\]
注意到分子和分母可通过在一段时间内积分求得联合概率密度。比如，我们有
\[p_{X_{n}|Y_{0:n}}\left ( x_{n};y_{0:n} \right ) =\frac{\int p_{X_{0:n},Y_{0:n}}\left ( x_{0:n},y_{0:n} \right )dx_{0:n-1} }{\int p_{X_{0:n},Y_{0:n}}\left ( x_{0:n},y_{0:n} \right )dx_{0:n}}
\]
说明：联合概率密度和条件概率密度的关系，分子积分后是 \(X_{n}\) 和 \(Y_{0:n}\) 的联合概率密度，而分母积分后是 \(Y_{0:n}\) 的联合概率密度，所以相除就是条件概率密度。这也是隐含马尔可夫的计算关键所在。
小结
本文只是隐含马尔可夫模型的基本介绍。从模型定义和概率密度计算方面做了一定程度的介绍，虽然公式比较多，估摸着大家应该能看懂，如有疑问可在评论区留言。其实重点还在于其原理的理解和应用。
