二维声波传播方程的有限差分模拟

本文首发于 算法社区 dspstack.com，转载请注明出处，谢谢。

二维声波传播方程的有限差分解法

• 二维声波方程在Oxz平面表示：
  
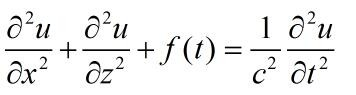
• 有限差分表示：
  

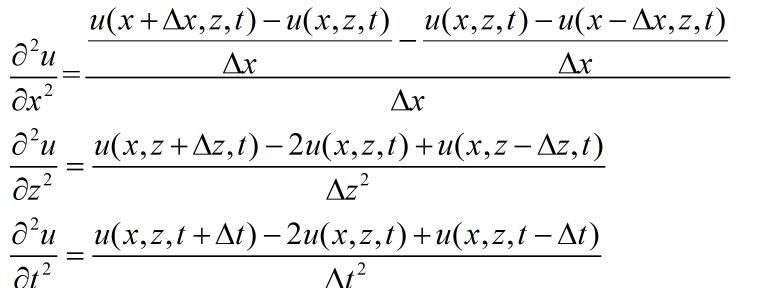
其中f(t)表示源函数，我们用Ricker作为激发源。

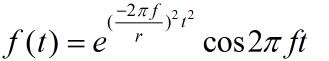
• 离散化的二维声波方程
  
• matlab示例
  x,z向共201个节点，节点间隔h=8m,时间采样点位400，采样间隔为0.001s。假设声音传播速度为3km/s，激发源在i=100,j=100处。Ricker主频为20Hz,频带控制参数r=3.

clc;
clear;
Nx=201; Nz=201; Nt=400;%设置采样点数，采样时间点数
h=8;    %x方向和z方向的步长
dt=0.001;   %时间步长
c=3000;    %波传播速度为3km/s
f=20;         %震源频率
gama=3;  %频带控制参数
A=(dt*c)^2/h^2;
u=zeros(Nx,Nz,Nt);
for k=2:Nt-1
    for i=3:Nx-2
        for j=3:Nz-2
            if i==100&j==100
                u(i,j,k+1)=exp(-(2*pi*f*k*dt/gama).^2).*cos(2*pi*f*k*dt);
        %在(100km，100km)处设置一个振动源
            else u(i,j,k+1)=A*(u(i+1,j,k)+u(i-1,j,k)+u(i,j+1,k)+u(i,j-1,k)-4*u(i,j,k))-u(i,j,k-1)+2*u(i,j,k);
            end
            u(3,j,k+1)=u(4,j,k+1);
        end
    end
end
filename='二维波场快照.gif';
for k=1:4:Nt
pcolor(u(:,:,k))
shading interp;
colormap('bone');
axis equal;
axis([0,200,0,200]);
set(gca,'Ydir','reverse');
xlabel('x'); ylabel('z');
title('顶部为自由边界条件，其他为透射边界的二维声波传播快照');
if(k==201) keyboard; end
f=getframe(gcf); % 捕获画面
imind=frame2im(f);
[imind,cm] = rgb2ind(imind,256);
   if k==1
        imwrite(imind,cm,filename,'gif', 'Loopcount',inf,'DelayTime',0.05); %采用延迟时间为0.05秒写入给定的文件
    else
        imwrite(imind,cm,filename,'gif','WriteMode','append','DelayTime',0.1); %采用延迟时间为0.1秒写入给定的文件
    end
 end

• 参考万永革地震学导论