Andrew Ng ML课程SVM部分学习记录——SVM核函数
核函数
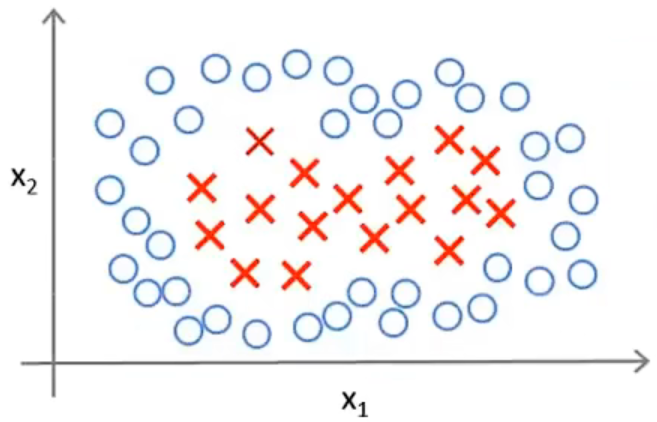
对于线性不可分的情况,可以借助核函数构造非线性分类器.
先选定部分标记点(landmarks)

对于一个样本\(x\),设\(f\)度量样本与标记点的相似度:
\[f_1={\mathbf {similarity}}(x,l^{(1)})=\exp(-\frac{\parallel x-l^{(1)}\parallel^2}{2\sigma^2})\\
f_2={\mathbf {similarity}}(x,l^{(2)})=\exp(-\frac{\parallel x-l^{(2)}\parallel^2}{2\sigma^2})\\
f_3={\mathbf {similarity}}(x,l^{(3)})=\exp(-\frac{\parallel x-l^{(3)}\parallel^2}{2\sigma^2})\\
\cdots
\]
这样的相似度函数被称作核函数,这里使用的是高斯核函数(Gaussian kernel function),实际上一眼就能看出这和高斯分布密度函数长得很像。
当\(x\rightarrow l^{(1)}\)时:
\[\lim_{x\rightarrow l^{(1)}}f_1=\exp(0)=1
\]
当\(\parallel x-l^{(1)}\parallel\gg 0\)时:
\[\lim f_1=\exp(-\infty)=0
\]
核函数的图像如下,分别对应\(\sigma=1,\sigma=2,\sigma=3\)的情况
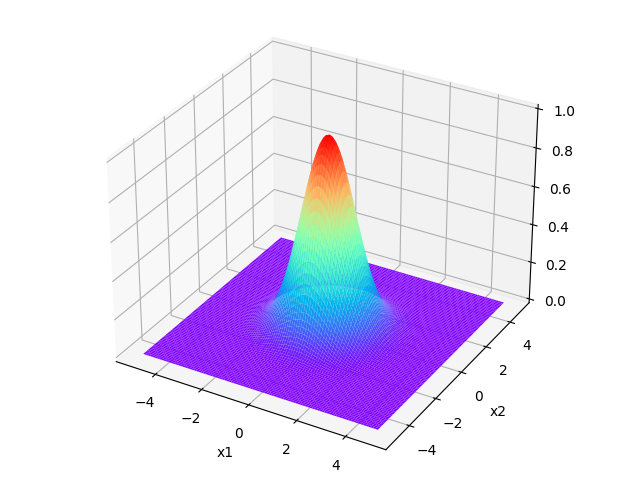
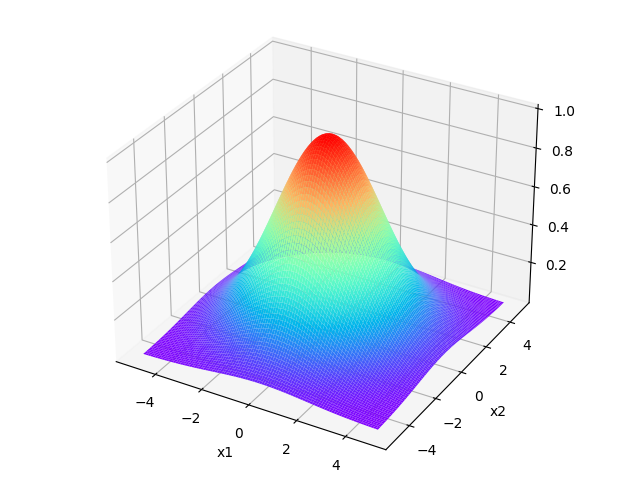
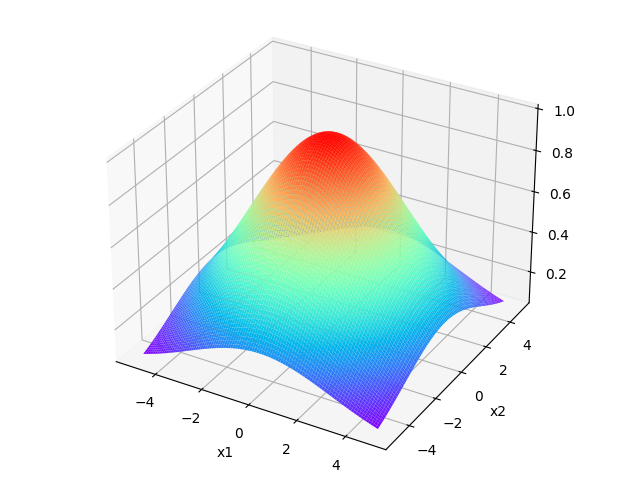
可以看出\(\sigma\)的值越大时,函数值(相似度)的下降越缓慢
令:
\[f=\left[
\begin{matrix}
f_0\\
f_1\\
f_2\\
\cdots\\
f_n
\end{matrix}
\right]
\]
这里\(f_0=1\),然后可以在代价函数中使用\(f\)代替\(x\)进行计算,决策边界形如:
\[\theta^Tf= 0
\]
标记点的选择
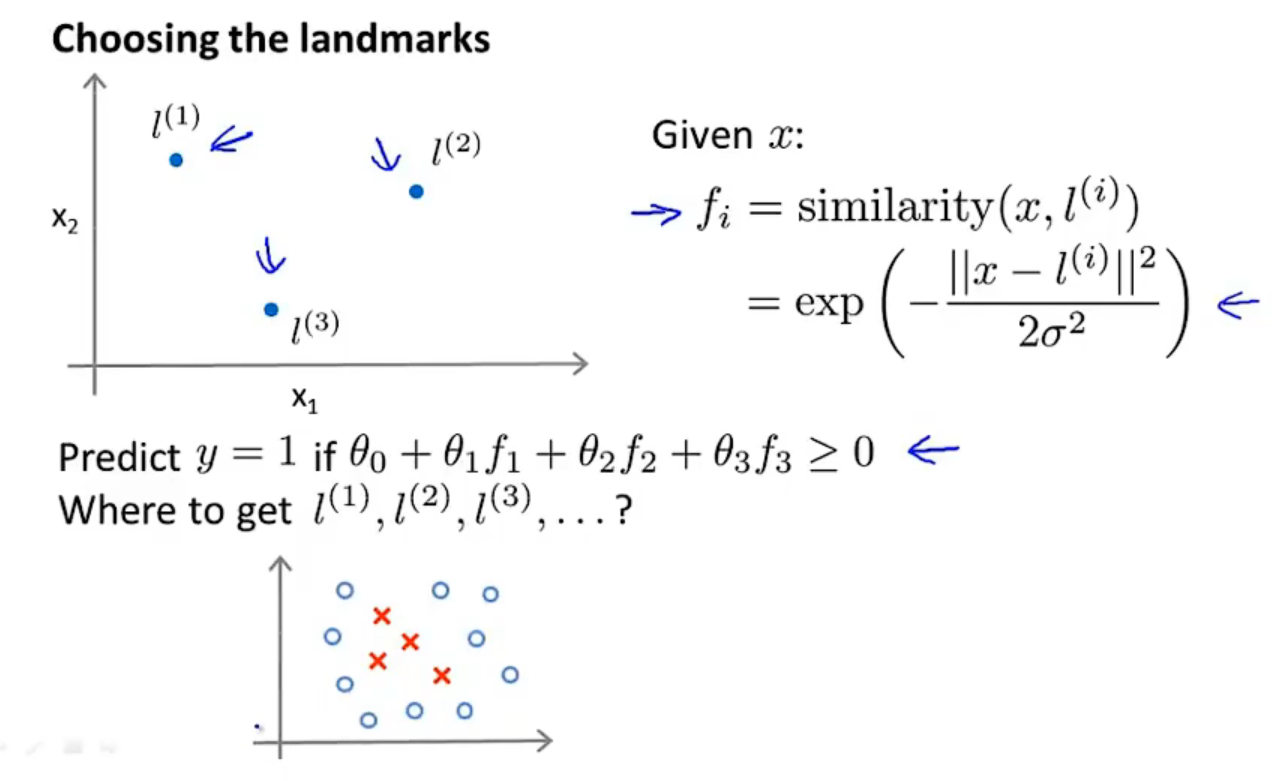
一种选择标记点的方法是,直接令\(l^{(i)}=x^{(i)}\),它对应的向量\(f\):
\[f^{(i)}=
\left[
\begin{matrix}
f_0^{(i)}\\
f_1^{(i)}\\
f_2^{(i)}\\
\cdots\\
f_i^{(i)}\\
\cdots\\
f_n^{(i)}
\end{matrix}
\right]
\]
其中\(f_0^{(i)}=f_i^{(i)}=1\)

