IEEE754标准 详解 转载
本文是我在学习IEEE754时找到的一篇微信文章,写的非常好,公众号是 二进制之路
本文原链接:https://mp.weixin.qq.com/s/mf1mH-aGWgcC6v2R8ijE8A
本文试图深入浅出的讲明白浮点数标准IEEE 754,并分析其精妙的设计原理。通过举例说明、回答为什么,带你渐进的了解浮点数的知识。
温馨提示:本文略为啰嗦,大约需要30分钟,还请耐心阅读,希望对你有所帮助。
十进制与二进制
说明:用小下标表示进制,无下标默认为十进制。例如十进制1表示为1或$ 1_{10} \(,二进制1表示为\) 1_2 $。
先来回顾一下十进制与二进制之间的转换,直接看例子不解释。
12.34 = $1 \times 10^1 $ + $2 \times 10^0 $ + $3 \times 10^{-1} $ + $4 \times 10^{-2} $ = 12.34
$ 101.11_2 $ = $1 \times 2^2 $ + $0 \times 2^1 $ + $1 \times 2^0 $ + $1 \times 2^{-1} $ + $1 \times 2^{-2} $ = 4 + 0 + 1 + 1/2 + 1/4 = 5.75
反过来:
5.75 = 5 + 3/4 = 4 + 1 + 2/4 + 1/4 = \(2^2\) + \(2^0\) + \(2^{-1}\) + \(2^{-2}\) = \(101.11_2\)
十进制小数点向左移动1位相当于将该数除以10,向右移动1位相当于将该数乘以10。
例如11/10=1.1,1.1$\times$10=11。
同理,二进制小数点向左移动1位相当于将该数除以2,向右移动1位相当于将该数乘以2。
例如$ 11_2 \(/2=\) 1.1_2 \(,\) 1.1_2 \times \(2=\) 11_2 $。
请熟记这个基础知识,我们下面还会用到。
科学记数法
科学记数法,是一种数字的表示法,最早由阿基米德提出。
通常,采用科学记数法来表示一个极大或极小的数。
- 一方面可以节省存储空间;
- 另一方面可以较为直观的确认它的大小(一个数的数量级、大小、精确度都较容易看出)。
例如:
0.00000000000000000000000167262158 = 1.67262158$ \times 10^{-24}$
1898130000000000000000000000 = 1.89813$ \times 10^{27}$
等号右边就是科学记数法的表示格式,即:\(a \times 10^n\),通常亦表示为aen。
其中:
- |a|>=1且|a|<10
- n为整数
二进制科学记数法
根据科学记数法的定义,如果用科学记数法来表示二进制数,格式为:
$ a \times 2^n $
其中:
- 指数基数为2
- |a|>=1且|a|<2,也就是说a的范围包含两个区间(-2,-1]、[1,2)
- n为整数
举几个例子,看看如何将二进制数表示为科学记数法的格式。
5.75 = \(101.11_2\) = $ 1.0111_2 \times 2^2 $ (小数点向右移动1位相当于将该数乘以2)
0.1875 = 3/16 = \(2^{-4}\) + \(2^{-3}\) = \(0.0011_2\) = \(1.1_2 \times 2^{-3}\) (小数点向左移动1位相当于将该数除以2)
浮点数
在计算器科学中,浮点是一种对于实数的近似值数值表示法,由一个有效数字(即尾数)加上幂数来表示,通常是乘以某个基数的整数次指数得到。以这种表示法表示的数值,称为浮点数。
可以简单理解为:浮点数是十进制科学记数法在计算机中的二进制表示,即二进制的科学记数法。
浮点数可以用来表示小数,极大或极小的数,占用存在空间少。
IEEE 754规定了四种表示浮点数值的方式
- 单精度(32位)
- 双精度(64位)
- 延伸单精度(43比特以上,很少使用)
- 延伸双精度(79比特以上,通常以80位实现)
二进制浮点数由三部分组成
- 符号位,0表示正数,1表示负数。
- 阶码,规定为实际指数值加上一个偏移值。偏移值为\(2^{n-1}-1\),其中的n为存储指数的比特位长度。
- 尾数,用于存储“有效数字”的小数部分,使用原码表示。

(图片来源:https://zh.wikipedia.org/wiki/IEEE_754)
下面我们将着重分析32位单精度浮点数,如无特殊说明,均针对单精度浮点数。
单精度浮点数,长度为32位:
- 最高的1位是符号位
- 接下来是8位阶码,偏移值为\(2^{8-1}-1=128-1=127\)
- 最后的23位是尾数。
举例说明
正数实例
1)将十进制数转换为浮点数
78 = \(01001110_2\) = \(1.001110_2 \times 2^6\)
分析:
78为正整数,所以符号位为0。
指数为6,因此阶码为6+127=133=\(10000101_2\)。
由于尾数只存储有效数字的小数部分,所以尾数为001110。最高位1规定不显式存储,以隐含方式存在,计算或恢复数值时再把这个1补上。
最终得到的32位浮点数表示为(分段显示方便阅读):
0-10000101-00111000000000000000000
2)将浮点数恢复为十进制数
0-10000101-00111000000000000000000
分析:
符号位为0,说明该数为正数。
阶码为10000101=133,因此实际指数值为133-127=6。
尾数=小数部分0.00111000000000000000000+隐含值1=1.00111000000000000000000。
因此,该浮点数所表示的实际数值为\(1.00111_2 \times 2^6\)=\(01001110_2\)=78
负数实例
将十进制数转换为浮点数:
-16 = \(10010000_2\) = \(-1.0 \times 2^4\) (用原码表示二进制)
分析:
符号位为1
阶码为4+127=131=\(10000011_2\)
尾数为0因此-16的单精度浮点数表示为:1-10000011-00000000000000000000000
浮点数表示步骤
- 将十进制数值转换为二进制数值。
- 将二进制数值转换为科学记数法。其中,二进制表示采用原码表示。
- 确定符号位:如果是正数,符号位为0;如果是负数,符号位为1。
- 计算阶码:将科学记数法的指数值加上偏移值(单精度为127),再转换为8位二进制。
- 计算尾数:忽略有效数字的整数部分1(小数点左边的1),将有效数字的小数部分(小数点右边的值)作为尾数,如果尾数不足23位则右边用0填充至23位。
上面说浮点数是二进制的科学记数法,可能有点不太严谨,但有时便于理解记忆更为重要。
好了,关于IEEE 754浮点数的介绍,我们下面正式开讲。
Why Why Why
重要的事情须问三遍,先来回答几个问题。
指数为什么要加上偏移值?
上面我们已经看到,指数存储的时候需要加上偏移值,但恢复的时候还得再减回来,来回捣腾是否有必要,是否可以直接存储指数,简单明了?
答案是肯定的。
但凡事都是两面的,有利必有弊。要理解这一点,我们得来看看为何要这样设计。
由于科学记数法的指数可为正,可为负。因此,一个数转换为浮点数之后,符号位、阶码这两部分都是带符号的。
如果我们要比较两个浮点数的大小,那么除了要判断比较数值本身的符号位,还需要再判断比较阶码的符号位,最后才是非符号部分的比较。显然,这会复杂化比较逻辑。
在使用了偏移值之后,无论指数部分是正是负,都可以转换为非负数。将真值映射到正数域的数值(真值在数轴上正向平移一个偏移量),称为移码。使用移码来比较两个真值的大小比较简单,只要高位对齐后逐位比较即可,不用考虑符号位问题。
另一个类似的问题是:计算机可以用原码存储负数吗?其实也是可以的,但这会给二进制的运算带来不便,还可能复杂化CPU指令集。
计算机为了设计简单,对于数值的加减运算都是带符号位的,减去一个正数相当于加上一个负数。因此,加法指令就可以实现数值的加减运算。。
如果使用原码进行运算,得到的结果可能是不正确的。例如1-1=\(00000001_2\)+\(10000001_2\)=-2。
而使用补码运算就可以解决这个问题。如果使用原码存储,在进行运算时再转为补码,计算后又要转为原码存储,那还不如直接用补码存储。
为什么偏移值为\(2^{n-1}-1\)而不是\(2^{n-1}\)?
8位二进制有符号数的取值范围是[-128,127],也是32位浮点数指数可能表示的最大取值范围。
8位二进制无符号数的取值范围是[0,255],也是32位浮点数阶码可能表示的最大取值范围。
要使指数为非负数,[-128,127]需要加上偏移值128,得到阶码是[0,255]。
IEEE 754规定阶码0和255为特殊值,有特殊含义(稍后再讲)。
那么,阶码实际能表示的范围是[1,254]。如果偏移值仍为128,那么指数范围变成[-127,126]。
为了让浮点数能够表示更大的取值范围,将指数范围加上1得到范围[-126,127],对应偏移值减去1得到127.
显然,最大指数值增大了,可以表示更大的数值|a|(数轴上离0更远,可以表示更大的值)。但同时,最小指数值也变大了,原来可以表示的最小数值|a|现在却表示不了了(数轴上离0更远,不能表示更小的值)。
那似乎能表示的区间(范围)并没有改变啊,你骗我!
无论如何,阶码的规定如下:
- 阶码的范围是:1 到 \(2^n-2\),对于单精度浮点数是:[1,254]
- 偏移值是:\(2^{n-1}-1\),对于单精度浮点数是:127
- 单精度的实际指数范围是[-126,127]
为什么隐含最高位1?
由于使用科学记数法表示二进制数值时,最高位为固定数值1。因此,通过省略最高位1,浮点数的尾数可以增加1位来更精确的表示数值(23位尾数,能表示24位二进制数)。
浮点数表示形式
前面对于浮点数的介绍,其实指的是浮点数的规格化表示形式。规格化形式,是浮点数最主要的表示形式,日常使用的绝大部分数值都可以用它来表示。
然而,还有一些特殊数值是规格化形式无法表示的,例如0、非常接近0数值。
浮点数的5种表示形式
| 浮点数形式 | 阶码 | 尾数 | 描述 |
|---|---|---|---|
| 零 | 0 | 0 | 阶码是0,尾数的小数部分是0,这个数是±0(正负取决于符号位) |
| 非规格化 | 0 | 非0 | 阶码是0,尾数的小数部分是非0,有效数字的整数部分为固定数值0。非规格化形式用于表示非常接近0的数。(指数偏移值为\(2^{n-1}-2\)) |
| 规格化 | [1,\(2^n-2\)] | 任意 | 阶码位不包含全0和全1,尾数的小数部分为任意数值。有效数字的整数部分为固定数值1,使用隐含的方式表示,因此尾数只存储有效数字的小数部分。(指数偏移值为\(2^{n-1}-1\)) |
| 无穷 | \(2^n-1\) | 0 | 阶码是\(2^n-1\)(阶码位全是1),尾数的小数部分是0,这个数是±∞(正负取决于符号位) |
| NaN | \(2^n-1\) | 非0 | 指数是\(2^n-1\),尾数的小数部分是非0,这个数表示为不是一个数(NaN) |
其中,n为存储指数的比特位长度,对于单精度浮点数n为8。
非规格化形式
一般是某个数字相当接近零时,才需要使用非规格化形式来表示。
IEEE 754标准规定:非规格化形式的浮点数的指数偏移值比规格化形式的浮点数的指数偏移值小1,也就是偏移值为\(2^{n-1}-2\)。
对于单精度浮点数,偏移值为126。因此,实际指数为固定数值-126(阶码0减去偏移值126)。
非规格化形式用于表示那些非常接近于零的数,解决填补了绝对值意义下最小规格数与零的距离,避免了突然式下溢出(abrupt underflow)。
单精度浮点数的各种极值情况
说明:为了方便描述,最大值与最小值指绝对值的大小
| 浮点数形式 | 正负号 | 有效数字 | 实际指数 | 表示数值 |
|---|---|---|---|---|
| 负无穷 | 1 | 1.0 | 128 | -∞ |
| 规格化最大值 | 1 | 2-\(2^{-23}\) | 127 | -(2-\(2^{-23}) \times 2^{127}\) = -3.4e+38 |
| 规格化最小值 | 1 | 1.0 | -126 | -\(2^{-126}\) = -1.18e-38(-1.17549435e-38) |
| 非规格化最大值 | 1 | 1-\(2^{-23}\) | -126 | -(1-\(2^{-23}) \times 2^{-126}\) = -1.18e-38(-1.17549421e-38) |
| 非规格化最小值 | 1 | \(2^{-23}\) | -126 | -\(2^{-23} \times 2^{-126}\) = -1.4e-45 |
| 负零 | 1 | 小数部分是0 | -127 | -0.0 |
| 正零 | 0 | 小数部分是0 | -127 | +0.0 |
| 非规格化最小值 | 0 | \(2^{-23}\) | -126 | \(2^{-23} \times 2^{-126}\) = 1.4e-45 |
| 非规格化最大值 | 0 | 1-\(2^{-23}\) | -126 | (1-\(2^{-23}) \times 2^{-126}\) = 1.18e-38(1.17549421e-38) |
| 规格化最小值 | 0 | 1.0 | -126 | \(2^{-126}\) = 1.18e-38(1.17549435e-38) |
| 规格化最大值 | 0 | 2-\(2^{-23}\) | 127 | (2-\(2^{-23}) \times 2^{127}\) = 3.4e+38 |
| 正无穷 | 0 | 小数部分是0 | 128 | +∞ |
| NaN | 0或1 | 小数部分非0 | 128 | NaN |
关于有效数字中\(2^{-23}\)是怎么来的,举个例子就明白了:
规格化最大值的有效数字=1.11...1(小数点后23个1)=2-0.00...01(小数点后22个0)=2-\(2^{-23}\)
浮点数小结
- 上面的表格从上往下,从负无穷到正无穷(NaN除外),浮点数集合的所有元素都是有序的。
- 规格化形式包含两个区间:[-3.4e+38,-1.18e-38], [1.18e-38,3.4e+38]。但无法表示相当接近0的区间:[0, ±1.18e-38)。
- 非规格化形式也包含两个区间:[-1.18e-38,-1.4e-45], [1.4e-45,1.18e-38]。相比规格化形式而言,可以表示更接近于0的数值。
- 非规格化最大值,与规格化最小值形成了平滑的过渡(相差\(2^{-149}\))。
- 浮点数区分正负0,但两者是相等的。在实际操作上存在一些差别,例如1.0/+0.0=+∞,1.0/-0.0=-∞。
在只有规格化形式的情况下,正数第1小、第2小、第3小和第4小分别为\(2^{-126}\)、\((1+2^{-23}) \times 2^{-126}\)、\((1+2 \times 2^{-23}) \times 2^{-126}\)、\((1+3 \times 2^{-23}) \times 2^{-126}\),两两之间的间距都是\(2^{-149}\)。
然而,规格化最小值与0的间距是\(2^{-126}\),\(2^{-126}\)比\(2^{-149}\)大了\(2^{23}\)倍。原来往0靠近的方向,数值都是逐渐减小的,但到了最小值\(2^{-126}\),下一个数突然就变成0了,这种情况被称为突然式下溢出(abrupt underflow)。
为了解决突然式下溢出(abrupt underflow)问题,IEEE采用了Intel公司力荐的渐进式下溢出(gradual underflow),在浮点数标准中对应的实现就是非规格化的表示形式。
非规格化形式的最小值与0的距离为\(2^{-149}\),刚好与规格化数值的最小间距相等,解决了突然式下溢至0的问题。
写到这里,得说一句我真没骗你!
前面提到为什么偏移值为\(2^{n-1}-1\)而不是\(2^{n-1}\)的时候,问题只解释了一半:对于32位浮点数,阶码实际能表示的范围是[1,254]。如果偏移值仍为128,那么指数范围变成了[-127,126]。为了让浮点数能够表示更大的取值范围,将指数范围加上1得到范围[-126,127],对应偏移值减去1得到127。
而关于另一半的解释,到这里才能说明,因为这关系到非规格化形式。
偏移值由128改为127,让规格化形式能够表示更大的数值。而更小的数值,则可以由非规格化形式来表示。前面已经分析,规格化与非规格化数值之间能够非常平滑的过渡,因为正的规格化最小值为\(2^{-126}\),正的非规格化最大值为(1-\(2^{-23}) \times 2^{-126}\),间距为\(2^{-149}\)。
借用一张图(From:http://senzhangai.github.io),在数轴上表示浮点数如下。
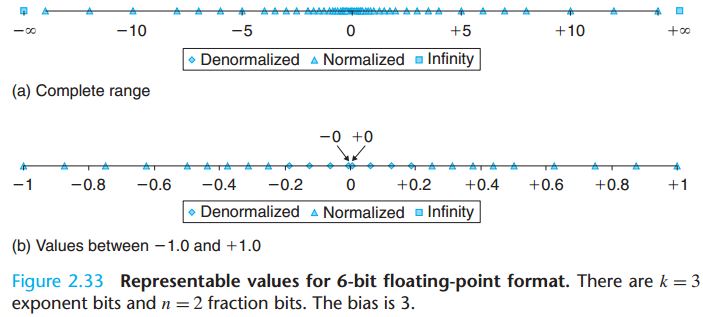
无穷大在两头,0与无穷大之间大部分是规格化数,只有非常接近0的小部分是非规格化数。而且,越是靠近0的地方,数与数之间的间隔越小。相反,越是往无穷大的地方,数与数之间的间隔越大。
当越过非规格式化最小值时,下溢到0。当越过规格式化最大值时,上溢到无穷大。
文章写到这里,终于可以感叹一句:真的是处处有学问,非常的精心设计。不得不说IEEE 754对浮点数的规定真的是相当的精巧、完美!!!
Java中的float
代码:
java
public static void main(String[] args) {
System.out.println(String.format("能表示的最小值:%s,规格化最小值:%s,能表示的最大值:%s", Float.MIN_VALUE, Float.MIN_NORMAL, Float.MAX_VALUE));
System.out.println(String.format("指数范围:[%s,%s]",Float.MIN_EXPONENT, Float.MAX_EXPONENT));
float underflow = Float.MIN_VALUE - ((Double) Math.pow(2, -149)).floatValue();
float overflow = Float.MAX_VALUE + ((Double) Math.pow(2, 103)).floatValue();
System.out.println(String.format("下溢出:%s,上溢出:%s", underflow, overflow));
}
输出结果:
能表示的最小值:1.4E-45,规格化最小值:1.17549435E-38,能表示的最大值:3.4028235E38
指数范围:[-126,127]
下溢出:0.0,上溢出:Infinity
最后,仍有一些想写还没写的内容,然而这篇已经耗费了大量精力,且文章冗长而啰嗦,咱们还是有空再续。
题图:senzhangai.github.io
参考
https://zh.wikipedia.org/wiki/IEEE_754
https://zh.wikipedia.org/zh-hans/浮点数
https://zh.wikipedia.org/wiki/科学记数法
https://zh.wikipedia.org/wiki/NaN
《Java虚拟机规范(Java SE 7)》
《深入理解计算机系统》第2版
《码出高效》Java开发手册



 浙公网安备 33010602011771号
浙公网安备 33010602011771号