HDOJ-三部曲一(搜索、数学)- A Knight's Journey

A Knight's Journey

Time Limit : 2000/1000ms (Java/Other)   Memory Limit : 131072/65536K (Java/Other)

Total Submission(s) : 51   Accepted Submission(s) : 17

Problem Description

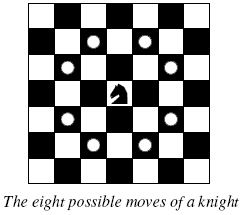Background The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans?
Problem Find a path such that the knight visits every square once. The knight can start and end on any square of the board.

 

Input

The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .

 

Output

The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number. If no such path exist, you should output impossible on a single line.

 

Sample Input

3 1 1 2 3 4 3

 

Sample Output

Scenario #1:

A1

 

Scenario #2:

impossible

 

Scenario #3:

A1B3C1A2B4C2A3B1C3A4B2C4

 

Source

PKU

 

 

第一次写深搜，感觉还不错

 

#include<iostream>
#include<cstring>
using namespace std;
int m,n;
int c;                                           //已走过的步数
bool f;                                          //标记是否找到答案了
int chess[30][30]={0};
int step[2][8]={{-1, 1,-2, 2,-2,2,-1,1},         //每一种可能的走法，注意要按字典序排列
                {-2,-2,-1,-1, 1,1, 2,2}};
char ans1[64];
int ans2[64];
bool move(int i,int j,int k)
{
	if(i+step[0][k]>=0&&i+step[0][k]<m&&j+step[1][k]>=0&&j+step[1][k]<n&&!chess[i+step[0][k]][j+step[1][k]])
	{
		chess[i+step[0][k]][j+step[1][k]]=1;
		return true;
	}
	else 
		return false;
}
void DFS(int i,int j)
{
	
	ans1[c]=j+'A';
	ans2[c]=i+1;

	if(c==m*n)                                    //找到结果，回退
	{
		f=true;
		return;
	}
	for(int t=0;t<8;t++)                         //尝试每一种走法
	{
		if(move(i,j,t))                        
		{
			c++;
			DFS(i+step[0][t],j+step[1][t]);
			if(c==m*n)                           //如果找到结果就一直回退
				return;
			chess[i+step[0][t]][j+step[1][t]]=0; //还原
			c--;
		}
	}
	return;
}

int main()
{
	int T;
	cin>>T;
	int t=T;
	while(T--)
	{
		int i,j,k;
		cin>>m>>n;		
		for(j=0;j<n;j++)
		{
			for(i=0;i<m;i++)
			{	
				c=1;
				memset(chess,0,sizeof(chess));
				chess[i][j]=1;
				f=false;	
				DFS(i,j);
				if(f)
				{
					cout<<"Scenario #"<<t-T<<":"<<endl;
					for(k=1;k<=m*n;k++)
						cout<<ans1[k]<<ans2[k];
					cout<<endl;
					break;
				}
			}
			if(f)
				break;
		}
		if(!f)
		{
			cout<<"Scenario #"<<t-T<<":"<<endl;
			cout<<"impossible"<<endl;
		}
		cout<<endl;
	}
}