傅里叶变换
傅里叶级数很容易理解,而傅里叶变换抽象许多。
傅里叶变换的目的在于,将图像从spatial domain变换到frequency domain。这样就能处理图像中特定频率的信息,并且可以通过傅里叶逆变换还原。
- 第一个角度
来自知乎回答,答主写得非常好,以下全文引用。
傅里叶变换就是除法.
首先通过一个简单的例子来看除法是如何实现变换的:
假设只存在五元和二元硬币,现在有人告诉你他有九块钱,你想知道他有什么硬币。这是一个从钱数到硬币个数的变换。(这里有个问题五元和二元不是正交基,只是方便理解)
9/5 =1余4 --> 包含一个5
4/2=2余0 --> 包含两个2
你立刻就知道他有一个(强度)五元(频率)和两个(强度)二元(频率)。
看,成功从金钱域变换到了硬币域。
傅里叶变换公式的这个写法非常的坑爹,好好的除法非要在指数上加负号!这就是所有不解的来源!
一切误会和不解的来源。
如果这样写:
这才是正确的写法,其中分母是频率为ω的圆周运动:
这就是频率为ω的圆周运动。
然后傅里叶变换就是在用除法求在f(t)中有多少频率为ω的圆周运动,然后把它们加起来,得到f(t)中所有频率ω的分布函数。
总结一下,通过积分,我们把t消除,得到了关于频率的函数,这也就是所有频率的分布函数。完美!
- 第二个角度,来自3b1b。
e^{-iwt} 可以看作在复平面上,以原点为中心,半径为1的一个圆的旋转,旋转的速度或者说,周期由wt决定。而写成wt,则是把t分离出来,w代表了wt/t。wt从0到2π代表旋转了一圈。
而Ce^{-iwt}代表把这个圆半径乘上C,就代表点到原点距离随着t也会改变。那么实际上我们有三个变量,复平面两个再加上t一个。这个时候可以把t拉上到z轴,我们得到了一个曲线,所以复平面上的点是曲线上某点在xy轴上的投影。
待分离频率的函数 f(t)e^{-iwt} 在w确定的情况下,正无穷到负无穷积分,得到的是曲线(不是螺旋,螺旋是C=常数时)在x轴上的投影。积t的分相当于投影到复平面XOY,而积分限关于t=0,x=0对称消去了虚部,也就是说我们实际上投影了两次,第一次在复平面上投影,第二次再把结果投影到x轴上。
- 第三个角度:
我们从傅里叶级数来看,一个连续无周期函数可以被分离成频率分布函数的积分,y轴是权值。如果是离散的,那么就是若干个频率的函数加权求和的结果。而这些函数之间两两正交,那么得到这些函数的分布就很简单,乘以本身再积分就能得到权值。那么我们观察傅里叶变换公式,也是一个意思,想得到某个频率F(w),那么就用原函数f(t)乘以对应的频率,再求积分。这个乘以对应角度2的旋转,积分对应角度2的求质心在x轴上的投影坐标。
- 补充:
实函数表示为傅里叶级数,傅里叶级数本身不包括虚数分量部分,它是角度2里面,旋转曲线在复平面投影的圆的实部,也就是圆的x轴投影。要用欧拉公式统一表示就会扩展到虚数部分,然后为了消去虚数部分,本身1到N的求和就变成了-N到N。变换到积分就是+无穷到-无穷,这样的话,y轴的分量就会完全抵消,也就是说虚部就消失了。(这里隐含的意思是,这个曲线的虚部y轴,关于t=0这个平面奇对称,也就是说幅度一样,方向相反。往上曲线旋转的方向和往下是相反的,这也可以通过欧拉公式得出。另外也可以通过:实函数的FT结果,实部是偶函数,虚部是奇函数,那么两边累加,奇函数相互抵消了)
- 最后总结:
傅里叶变换精确地还原出了原函数的频谱分布。
-
连续函数傅里叶变换:对原函数有限时长的采样导致频谱取值范围无限,除非有限时间内正好得到了原函数的整数个周期(前提是原函数是周期函数,并且是band-limited)。因为连续不可导的两个边沿需要无穷多个频率分量来拟合。
-
DFT:对原函数采样的频率越高,频谱的取值范围就越大,这个可以用采样定理理解。采样时间越长,频谱的精度越高。这个和前面这部分对称的。



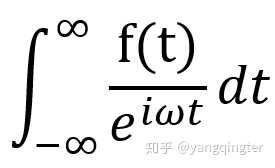
 这就是频率为ω的圆周运动。
这就是频率为ω的圆周运动。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号