循环队列的实现

用数组和链表都可以实现队列，其中用数组实现的队列是顺序队列，用链表实现的队列是链式队列。顺序队列和链式队列的实现都比较好理解。

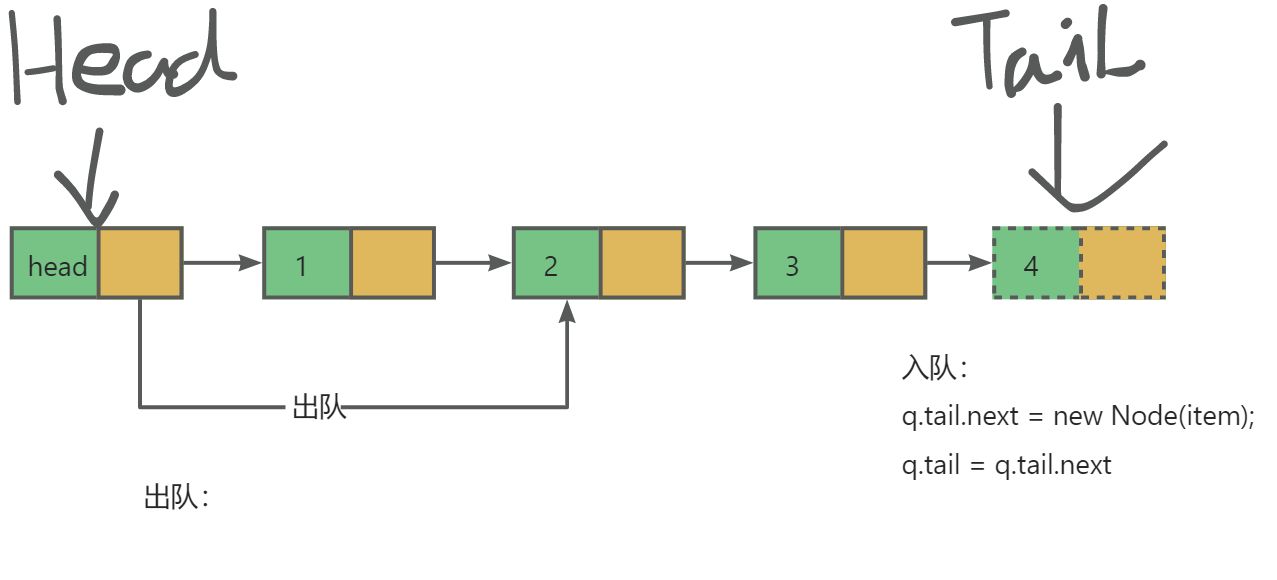
链式队列

链式队列比较好实现。

package linked_quque

import (
	"fmt"
	"log"
	"tx-algorithm/linkedList"
)

type LinkedQueue struct {
	n     uint32               // 队列的大小
	count uint32               // 队列中元素的数量
	head  *linkedList.ListNode // 指向队头的指针
	tail  *linkedList.ListNode // 指向队尾的指针
}

func NewLinkedQueue(n uint32) LinkedQueue {
	list := linkedList.NewLinkedList()
	return LinkedQueue{n: n, head: list.GetHead(), tail: list.GetHead()}
}

// enqueue 链式队列的入队就不需要像顺序队列那样迁移数组的操作
func (q *LinkedQueue) enqueue(item int) {
	if q.count == q.n {
		log.Println("queue is full")
		return
	}

	// 链表最后添加元素且将tail指针新添加的元素
	q.tail.SetNext(linkedList.NewListNode(item))
	q.tail = q.tail.GetNext()
	q.count++
}

// dequeue 出队时间复杂度O(1)
func (q *LinkedQueue) dequeue() any {
	if q.head.GetNext() == nil {
		log.Println("queue is empty")
		return nil
	}

	s := q.head.GetNext().GetValue()
	q.head.SetNext(q.head.GetNext().GetNext())
	q.count--
	return s
}

func (q *LinkedQueue) ls() {
	cur := q.head.GetNext()
	for cur != nil {
		fmt.Printf("%v ", cur.GetValue())
		cur = cur.GetNext()
	}
	fmt.Println()
}

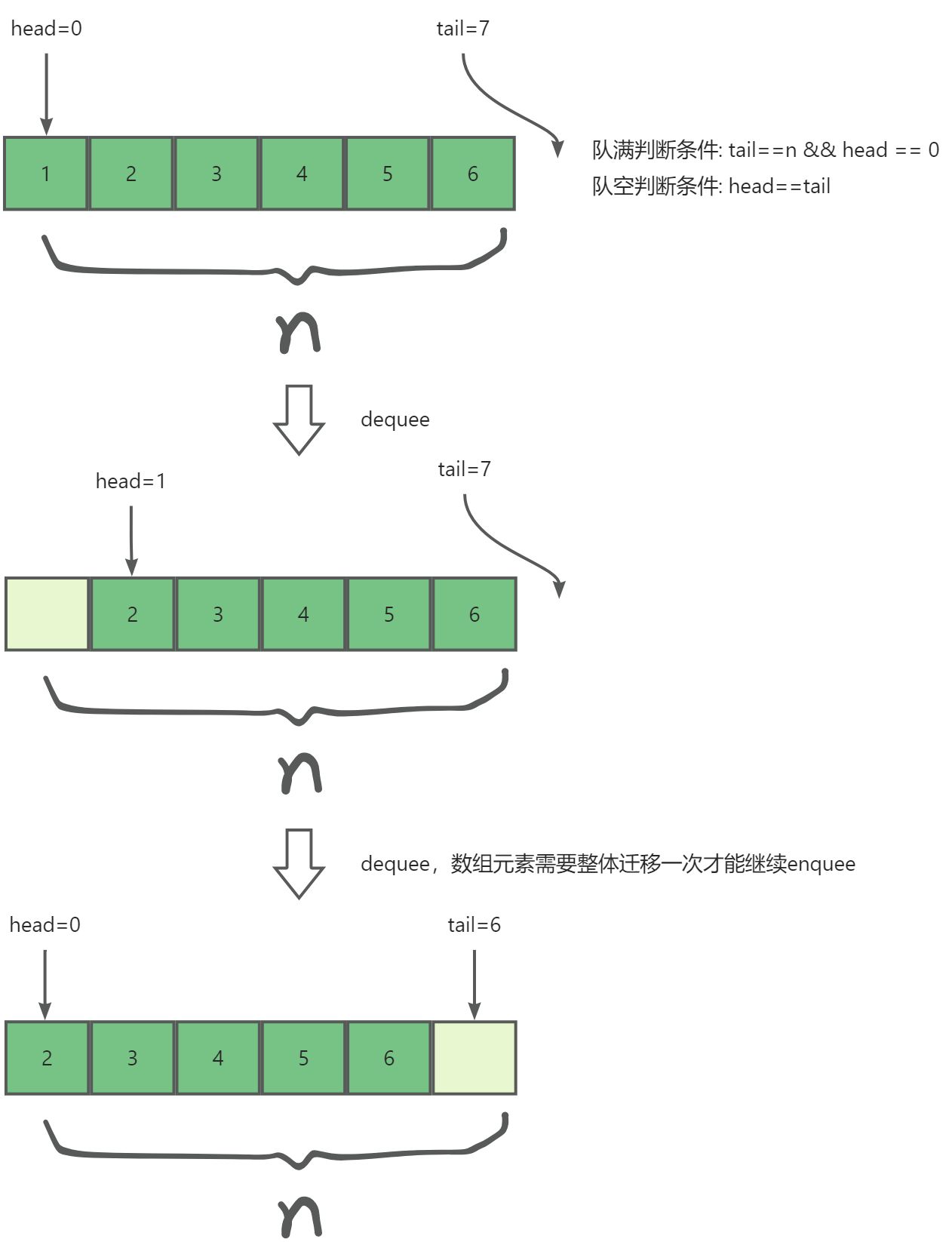
顺序队列

数组实现顺序队列稍微麻烦一些，主要是当有出队导致数组前面空了且数组后面满了的时候需要将数组整体迁移一次才能入队。

package array_queue

import (
	"fmt"
	"log"
)

type ArrayQueue struct {
	items []int // 存储队列元素的数组
	n     int   // 队列的大小
	head  int   // 队头下标
	tail  int   // 队尾下标
}

func NewArrayQueue(n int) ArrayQueue {
	return ArrayQueue{items: make([]int, n, n), n: n, head: 0, tail: 0}
}

// enqueue 入队的时间复杂度均摊后是O(1)
func (q *ArrayQueue) enqueue(item int) {
	if q.tail == q.n && q.head == 0 {
		log.Println("queue is full")
		return
	}

	// 虽然q.tail==q.n，但是其实此时队头那边是空的，可以进行一次数据迁移
	if q.tail == q.n {
		for i := q.head; i < q.tail; i++ {
			q.items[i-q.head] = q.items[i]
		}
		q.tail -= q.head
		q.head = 0
	}

	q.items[q.tail] = item
	q.tail++
}

// dequeue 出队时间复杂度O(1)
func (q *ArrayQueue) dequeue() int {
	if q.head == q.tail {
		log.Println("queue is empty")
		return -1
	}

	r := q.items[q.head]
	q.head++
	return r
}

func (q *ArrayQueue) ls() {
	for i := q.head; i < q.tail; i++ {
		fmt.Println(q.items[i])
	}
}

循环队列

循环队列避免了顺序队列中会出现的数组迁移的问题，同时又比链式队列更节约空间，因此更受青睐。

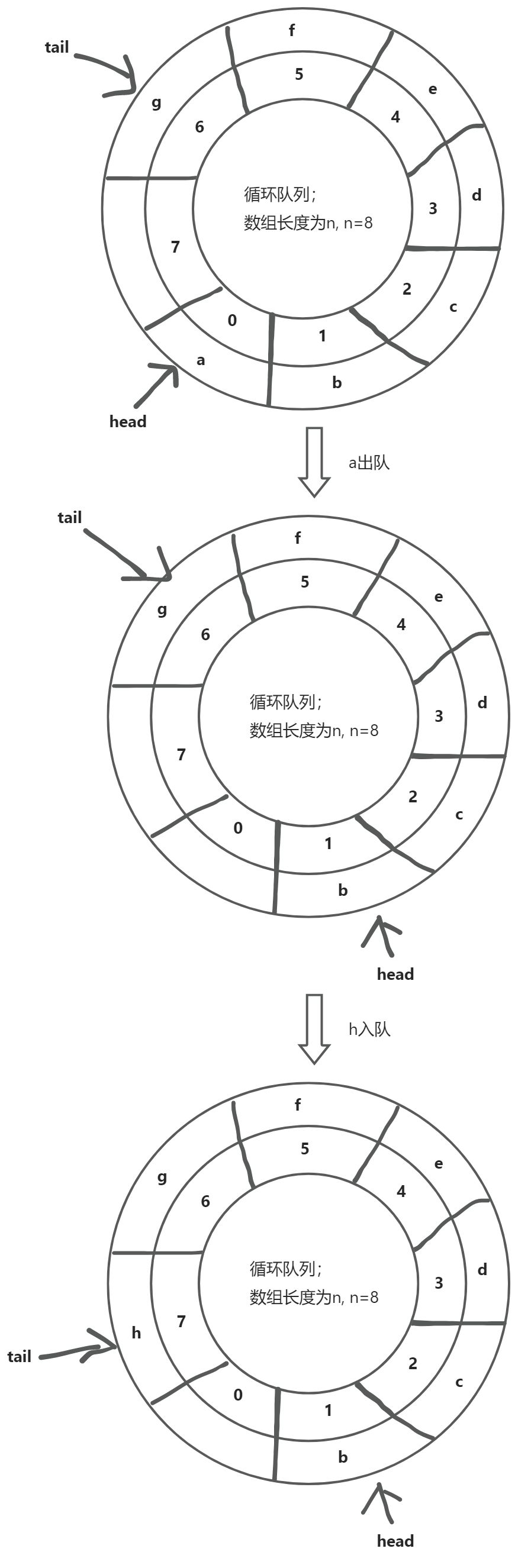
从上面的图可以清晰的看到循环队列的出入队机制，这里的难点在于如何判断循环队列的队空和堆满。同时可以看到在循环队列中tail指向的位置始终是空的，也就是始终会浪费数组的一个位置。
队空：head == tail
队满：(tail + 1) % n = head，为什么要做取模运算？考虑当tail7时,tail+18。而在循环队列中tail+1英爱等于0，所以这里需要取模。

package circular_queue

import (
	"fmt"
	"log"
)

type CircularQueue struct {
	items []int // 存储队列元素的数组
	n     int   // 队列的大小
	head  int   // 队头下标
	tail  int   // 队尾下标
}

func NewCircularQueue(n int) CircularQueue {
	return CircularQueue{items: make([]int, n, n), n: n, head: 0, tail: 0}
}

// enqueue 循环队列就不会涉及到到数组迁移的操作，注意这里的判满条件及入队后q.tail的变化
func (q *CircularQueue) enqueue(item int) {
	if (q.tail+1)%q.n == q.head {
		log.Println("queue is full")
		return
	}

	q.items[q.tail] = item
	q.tail = (q.tail + 1) % q.n
}

// dequeue 出队时间复杂度O(1)，注意这里出队以后q.head的变化
func (q *CircularQueue) dequeue() int {
	if q.head == q.tail {
		log.Println("queue is empty")
		return -1
	}

	r := q.items[q.head]
	q.head = (q.head + 1) % q.n
	return r
}

func (q *CircularQueue) ls() {
	for i := q.head; i != q.tail; {
		fmt.Printf("%v ", q.items[i])
		i = (i + 1) % q.n
	}
	fmt.Println()
}

参考

原文链接