走进JDK(十二)------TreeMap

一、类定义

TreeMap的类结构：

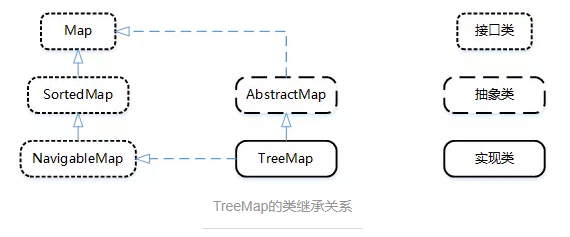
public class TreeMap<K,V> extends AbstractMap<K,V> implements NavigableMap<K,V>, Cloneable, java.io.Serializable

• TreeMap 是一个有序的key-value集合，它是通过红黑树实现的。
• TreeMap 继承于AbstractMap，所以它是一个Map，即一个key-value集合。
• TreeMap 实现了NavigableMap接口，意味着它支持一系列的导航方法。比如返回有序的key集合。
• TreeMap 实现了Cloneable接口，意味着它能被克隆。
• TreeMap 实现了java.io.Serializable接口，意味着它支持序列化。

 

二、成员变量、构造函数

    // 用于接收外部比较器，插入时用于比对元素的大小
    private final Comparator<? super K> comparator;
    // 红黑树的根节点
    private transient Entry<K,V> root;
    // 树中元素个数
    private transient int size = 0;

    private transient int modCount = 0;

// 默认构造函数。使用该构造函数，TreeMap中的元素按照自然排序进行排列。
TreeMap()

// 创建的TreeMap包含Map
TreeMap(Map<? extends K, ? extends V> copyFrom)

// 指定Tree的比较器
TreeMap(Comparator<? super K> comparator)

// 创建的TreeSet包含copyFrom
TreeMap(SortedMap<K, ? extends V> copyFrom)

 TreeMap跟HashMap等都是一样，内部的节点用Entry所表示，来看看TreeMap的Entry

static final class Entry<K,V> implements Map.Entry<K,V> {
    K key;
    V value;
    Entry<K,V> left;
    Entry<K,V> right;
    Entry<K,V> parent;
    boolean color = BLACK;
    
    // 其他省略
}

 

 三、源码解析

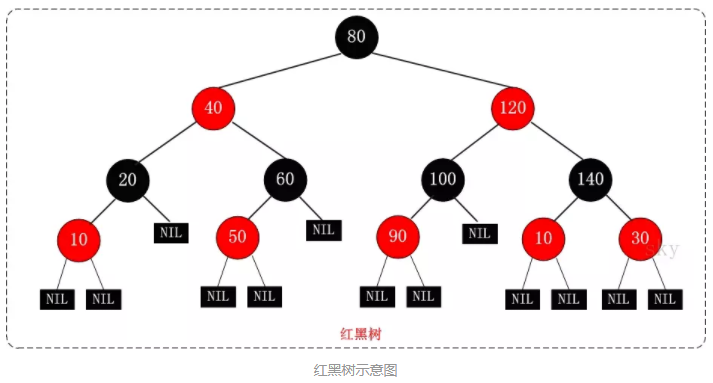
 TreeMap的实现是基于红黑树的结构，那么啥是红黑树？什么是红黑树

 1、put()

    // 将“key, value”添加到TreeMap中
    // 理解TreeMap的前提是掌握“红黑树”。
    // 若理解“红黑树中添加节点”的算法，则很容易理解put。
    public V put(K key, V value) {
        Entry<K,V> t = root;
        // 若红黑树为空，则插入根节点
        if (t == null) {
            root = new Entry<K,V>(key, value, null);
            size = 1;
            modCount++;
            return null;
        }
        int cmp;
        Entry<K,V> parent;
        Comparator<? super K> cpr = comparator;
        // 在二叉树(红黑树是特殊的二叉树)中，找到(key, value)的插入位置。
        // 红黑树是以key来进行排序的，所以这里以key来进行查找。
        if (cpr != null) {
            do {
                //记录当前的父节点，从根节点开始
                parent = t;
                cmp = cpr.compare(key, t.key);
                //插入的key小于当前父节点的key，继续比对left节点
                if (cmp < 0)
                    t = t.left;
                //右节点赋值给t，继续循环
                else if (cmp > 0)
                    t = t.right;
                else
                    //key值相等，将value覆盖之前的value
                    return t.setValue(value);
            //当t为null，说明已经是最后一个节点了
            } while (t != null);
        }
        else {
            if (key == null)
                throw new NullPointerException();
            Comparable<? super K> k = (Comparable<? super K>) key;
            do {
                parent = t;
                cmp = k.compareTo(t.key);
                if (cmp < 0)
                    t = t.left;
                else if (cmp > 0)
                    t = t.right;
                else
                    return t.setValue(value);
            } while (t != null);
        }
        // 新建红黑树的节点(e)
        Entry<K,V> e = new Entry<K,V>(key, value, parent);
        if (cmp < 0)
            parent.left = e;
        else
            parent.right = e;
        // 红黑树插入节点后，不再是一颗红黑树；
        // 这里通过fixAfterInsertion的处理，来恢复红黑树的特性。例如左旋、右旋、变色等等，这块比较复杂，有兴趣的可以自己看源码。初步接触可以理解恢复红黑树的特性就好。
        fixAfterInsertion(e);
        //新加一个节点，size自然+1
        size++;
        modCount++;
        return null;
    }

2、get()

    //根据给定的key值获取到TreeMap中的节点，然后取这个节点的value值。
    public V get(Object key) {
        Entry<K,V> p = getEntry(key);
        return (p==null ? null : p.value);
    }
    final Entry<K,V> getEntry(Object key) {
        //如果有比较器的话，走比较器的比较方法，去寻找到对应的节点
        if (comparator != null)
            return getEntryUsingComparator(key);
        if (key == null)
            throw new NullPointerException();
        @SuppressWarnings("unchecked")
        //如果不是使用Comparator参数构造器初始化TreeMap的话，往TreeMap中插入的key必须要实现Comparable接口
        Comparable<? super K> k = (Comparable<? super K>) key;
        Entry<K,V> p = root;
        while (p != null) {
            int cmp = k.compareTo(p.key);
            if (cmp < 0)
                p = p.left;
            else if (cmp > 0)
                p = p.right;
            else
                return p;
        }
        return null;
    }
    //这个在put()里面已经介绍过
    final Entry<K,V> getEntryUsingComparator(Object key) {
        @SuppressWarnings("unchecked")
        K k = (K) key;
        Comparator<? super K> cpr = comparator;
        if (cpr != null) {
            Entry<K,V> p = root;
            while (p != null) {
                int cmp = cpr.compare(k, p.key);
                if (cmp < 0)
                    p = p.left;
                else if (cmp > 0)
                    p = p.right;
                else
                    return p;
            }
        }
        return null;
    }

3、remove()

    public V remove(Object key) {
        Entry<K,V> p = getEntry(key);
        if (p == null)
            return null;

        V oldValue = p.value;
        //删除节点的方法
        deleteEntry(p);
        return oldValue;
    }
    private void deleteEntry(Entry<K,V> p) {
        modCount++;
        size--;
        //情况一：待删除的节点有两个孩子
        if (p.left != null && p.right != null) {
            //找右子树中最小元素节点
            Entry<K,V> s = successor(p);
            p.key = s.key;
            p.value = s.value;
            p = s;
        } 
        Entry<K,V> replacement = (p.left != null ? p.left : p.right);

        //情况二：待删除节点只有一个孩子
        if (replacement != null) {        
            replacement.parent = p.parent;
            if (p.parent == null)
                root = replacement;
            else if (p == p.parent.left)
                p.parent.left  = replacement;
            else
                p.parent.right = replacement;

            p.left = p.right = p.parent = null;

            if (p.color == BLACK)
                fixAfterDeletion(replacement);
        } 
        //情况三：根节点
        else if (p.parent == null) { 
            root = null;
        } 
        //情况四：无任何孩子节点
        else { 
            if (p.color == BLACK)
                fixAfterDeletion(p);

            if (p.parent != null) {
                if (p == p.parent.left)
                    p.parent.left = null;
                else if (p == p.parent.right)
                    p.parent.right = null;
                p.parent = null;
            }
        }
    }
    static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
        if (t == null)
            return null;
        else if (t.right != null) {// 找右子树中最小元素节点
            Entry<K,V> p = t.right;
            while (p.left != null)
                p = p.left;
            return p;
        } else {// 下面这段代码根本走不到，因为deleteEntry在调用此方法时传过来的t非null
            Entry<K,V> p = t.parent;
            Entry<K,V> ch = t;
            while (p != null && ch == p.right) {
                ch = p;
                p = p.parent;
            }
            return p;
        }
    }

删除的流程有点复杂，解释如下：

红黑树的删除分两步：
（1）以二叉查找树的方式删除节点。
（2）恢复红黑树的性质。

删除分为四种情况：
1、树只有根节点：直接删除即可。
2、待删除节点无孩子：直接删除即可。
3、待删除节点只有一个孩子节点：删除后，用孩子节点替换自己即可。
4、待删除节点有两个孩子：删除会复杂点。

针对第一种情况以及第二种情况，很简单，直接删；第三种情况也比较简单，只是多一个步骤，删除了当前节点之后，用孩子节点替换自己，自己离任，得找个接班人；第四种情况如下图所示：

假设我们要删除节点2：

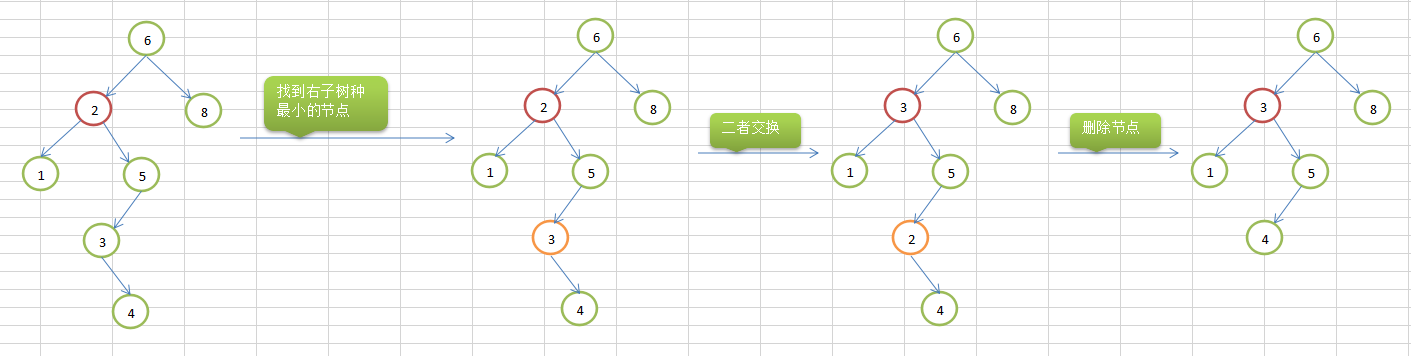
首先找到右子树最小的节点，然后将此节点与要删除的节点对换，对换不会影响二叉树的特性，这里分析一下，5节点的左子节点以及该字节点所有的孩子节点都会比5小，并且5节点的最小左节点肯定是大于要删除的节点2，因为二叉查找树的特性决定。

可以更简单的理解，任何一个节点，它的左节点底下所有的节点都会比它小，它的右节点下的所有节点都会比它大。