Lightoj 1090 - Trailing Zeroes (II)

题目连接：

　　http://www.lightoj.com/volume_showproblem.php?problem=1090

题目大意：

　　给出n,r,p,q四个数字1<=n,r,p,q<=1000000，求出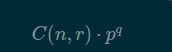的末尾有几个0？

解题思路：

　　是不是一下子懵了，数字好大，复杂度好高，精度怎么办···············，就问你怕不怕？

　　其实都是纸老虎啦，因为10的因子只有2和5，所以可以打表保存从1到当前数字相乘的积中分别含有2，5的个数。然后算出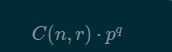中分别含有2，5的个数，取其最小就是结果。（ps：一定不要因为直接统计10的个数方便，而去统计10的个数，两者还是有不同的）。

#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
//复杂度O(1)
const int maxn = 1000010;
struct node
{
    int x, y;
};
node a[maxn];
int main ()
{
    int t, n, r, p, q, l = 1;
    memset (a, 0, sizeof(a));
    int x , y;
    x = y = 0;
    for (int i=2; i<maxn; i++)
    {//打表大法好\(^o^)/~
        int num = i;
        while (num % 2 == 0)
        {
            x ++;
            num /= 2;
        }
        num = i;
        while (num % 5 == 0)
        {
            y ++;
            num /= 5;
        }
        a[i].x = x;
        a[i].y = y;
    }
    scanf ("%d", &t);
    while (t --)
    {
        scanf ("%d %d %d %d", &n, &r, &p, &q);
        int res = min(a[n].x - a[r].x - a[n-r].x + (a[p].x - a[p-1].x) * q, a[n].y - a[r].y - a[n-r].y + (a[p].y - a[p-1].y) * q);
        printf ("Case %d: %d\n", l++, res);
    }
    return 0;
}