FIR数字信号滤波器

数字滤波器
在信号处理领域中,对于信号处理的实时性、快速性的要求越来越高。而在许多信息处理过程中,如对信号的过滤、检测、预测等,都要广泛地用到滤波器。
其中数字滤波器具有稳定性高、精度高、设计灵活、实现方便等许多突出的优点,避免了模拟滤波器所无法克服的电压漂移、温度漂移和噪声等问题,因而随着数字技术的发展,用数字技术实现滤波器的功能越来越受到人们的注意和广泛的应用。其中有限冲激响应(FIR)滤波器能在设计任意幅频特性的同时保证严格的线性相位特性,在语音、数据传输中应用非常广泛。
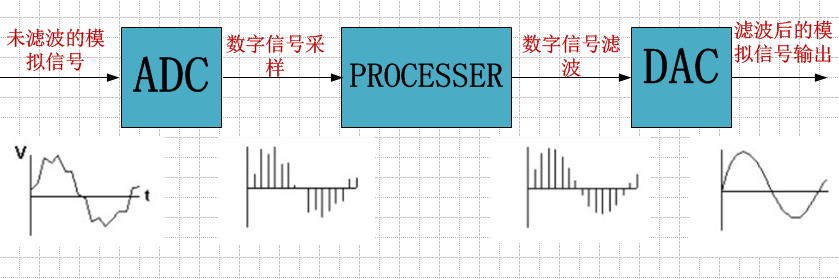
在信号处理中,滤波器的设计是非常重要的一个环节。滤波器的作用是什么?滤波器的作用就是把噪音去掉,把感兴趣的信号从大量信号中提取出来。
滤波器分两大类,一种是模拟(ANALOG)滤波器,另外一种是数字(DIGITAL)滤波器。模拟(ANALOG)滤波器是由模拟电路构成,而数字(DIGITAL)滤波器是由数字处理集成电路模块(DSP)和相应的软件构成。
数字(DIGITAL)滤波器是可编程的,所以相对于模拟(ANALOG)滤波器有很多优点。其中最大的优点是通过改变程序或改变程序变量就可设计出不同特点的滤波器,而且数字滤波器可以精确的处理低频率信号。
前面我们提到,什么是滤波器?滤波器就是把噪音去掉,把感兴趣的信号,或者说我们感兴趣的频率信号,从大量信号中提取出来。这如果要用数学语言来表达,那么就是用一个期望的频率特征函数H(f)去乘以输入信号频率X(f)。我们知道,输入信号是有时间性的,它是随着时间的改变而改变。就是说信号是发生在时间空间(时空,TIME DOMAIN)里的,那么,“期望的频率特征函数H(f)去乘以输入信号频率X(f)”这个数学表达在时间空间里是怎样的一个表达式呢?根据傅立叶变换定律,“期望的频率特征函数H(f)去乘以输入信号频率X(f)”在时间空间里就是“这个期望的频率特征函数H(f)在时间空间里的表达式h(t)去和输入信号x(t)做一个卷积”。
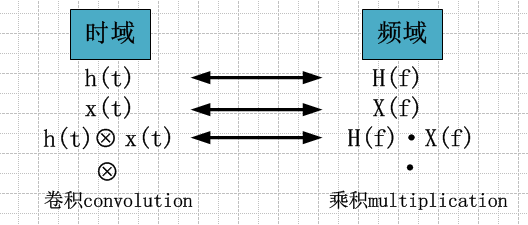
具体什么是卷积?用一句经典的话概括:卷积就是各个时刻的输入信号各自乘以相对应的衰减或增幅,然后叠加在一起作为输出信号输出,这里的衰减或增幅就对应与系统的单位冲激响应。——加权叠加。
物理意义:
卷积的重要的物理意义是:一个函数(如:单位响应)在另一个函数(如:输入信号)上的加权叠加。
详细的卷积原理可参考知乎网上的介绍,里面举了非常详细的例子介绍。
卷积讲解可参考:http://blog.csdn.net/bitcarmanlee/article/details/54729807
卷积的应用
用一个模板和一幅图像进行卷积,对于图像上的一个点,让模板的原点和该点重合,然后模板上的点和图像上对应的点相乘,然后各点的积相加,就得到了该点的卷积值。对图像上的每个点都这样处理。由于大多数模板都是对称的,所以模板不旋转。卷积是一种积分运算,用来求两个曲线重叠区域面积。可以看作加权求和,可以用来消除噪声、特征增强。
FIR滤波器是非递归型滤波器的简称,又叫有限长单位冲激响应滤波器。带有常系数的FIR滤波器是一种LTI(线性时不变)数字滤波器。冲激响应是有限的意味着在滤波器中没有发反馈。长度为N的FIR输出对应于输入时间序列x(n)的关系由一种有限卷积和的形式给出,具体形式如下:
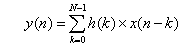
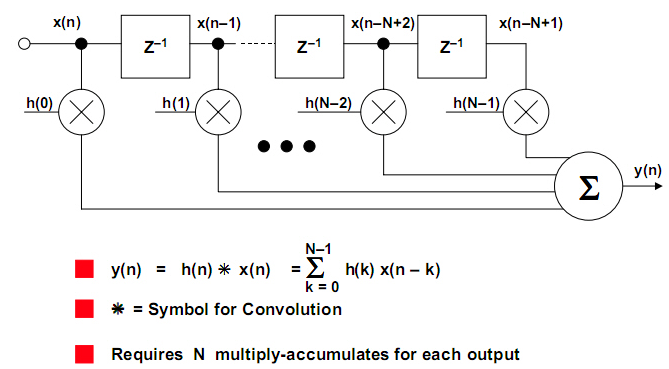
直接形式FIR滤波器图解:

输入信号是有时间性的,随着时间的改变而改变,FIR滤波器最终的输出是各个时刻的输入乘以相应的权重(系数),然后进行叠加,输出。
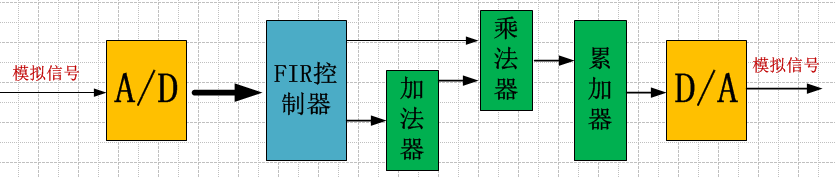
FIR原理
FIR数字滤波器“移动平均数”为例子:
“移动平均数”就是按我们事先设定的信号个数将输入信号加以平均。譬如,如果我们按每4个信号就做一次平均,那么这个4点的“移动平均数”滤波器就如下图所示:

下图是经过11点和51点“移动平均数”滤波器过滤的信号图:
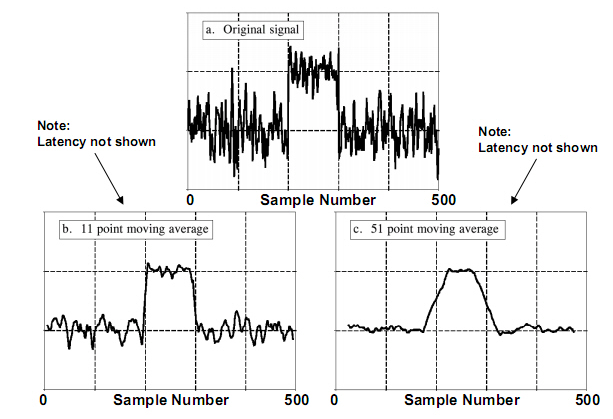
“移动平均数”滤波器的频率响应如下图所示:
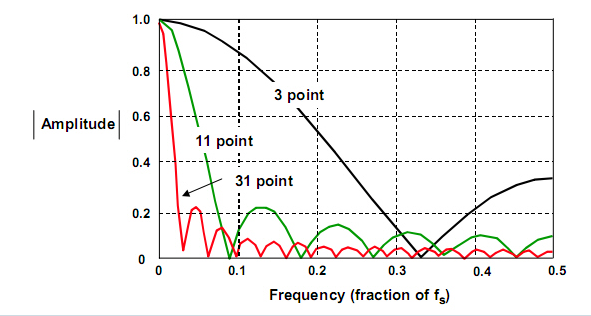
如上图所示,随着点数的增加,滚降(ROLLOFF)变陡了,但对旁瓣(sidelobe,衰减部分)的高低影响不大。但是如果我们考虑对滤波器的每个系数采用不同的权重(加权),而不是像“移动平均数”滤波器那样,用相同的权重(1/4,对4点“移动平均数”滤波器来说),那么可以期待旁瓣的大小会大大的降低。
对系数采用不同权重的滤波器,我们可以用下面的数学公式来表达:
这就是FIR数字滤波器的一般表达式。
下面我们以设计一个低通滤波器(LPF)为例,来说明FIR数字滤波器窗函数法的设计要点。
假设采样频率为Fs,滤波器的截止(CUT-OFF)频率为Fco,滤波器的长度为Nfir,那么用图形表示出来就如下图所示:

假设Nfir=128,Nco=13 注:Fco=Fs*(Nco/Nfir),h(t)的计算为:

那么这个低通滤波器的有限冲激响应就如下图所示:
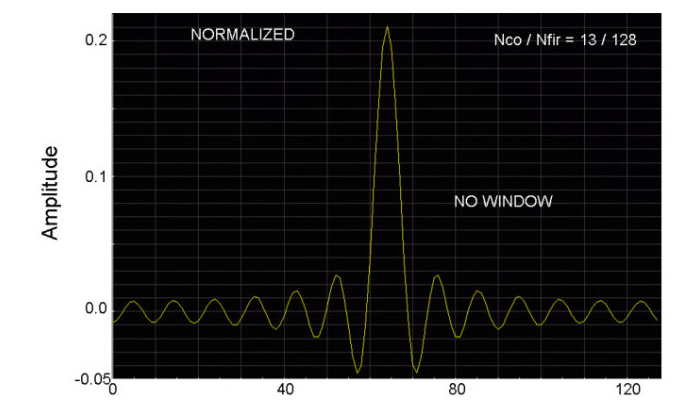
这样我们就设计出了一个FIR低通滤波器。为了检测这个滤波器的性能,我们用信号发生器产生包含从直流到频率为采样频率的一组信号,如下图所示:
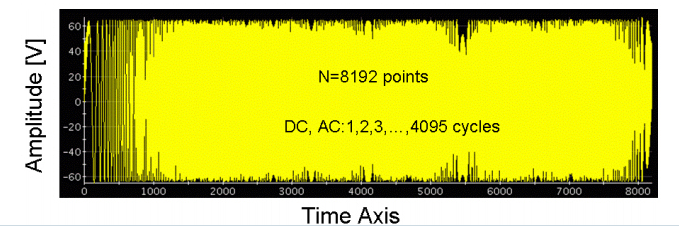
我们把这组信号与前面设计的FIR低通滤波器做卷积运算,并将结果(输出)进行快速傅立叶变换(FFT),得到的频率响应如下图所示:
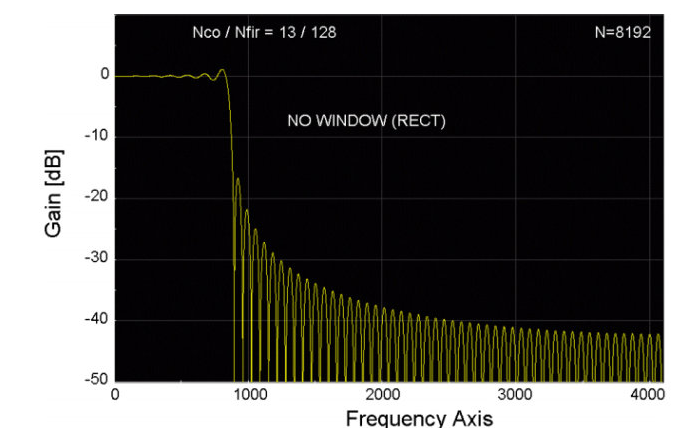
除了以上方法获得加权系数(抽头系数)外,还可以通过MATLAB获取。
总之,FIR滤波器的目的是滤除不需要的成分,留下需要的成分,如何留下就是通过加权叠加的方式实现。
滤波器除了低通外,还有高通,带通及带阻。
参考文献:http://blog.sina.com.cn/s/blog_74504f8f0100p5ub.html
FIR滤波器设计方法:
-
-
直接窗函数设计方法
-
等波纹设计方法
-
版权所有权归卿萃科技 杭州FPGA事业部,转载请注明出处



 浙公网安备 33010602011771号
浙公网安备 33010602011771号