51. 小蜜蜂

51. 小蜜蜂

一只小蜜蜂在如下图所示的蜂窝上爬行。它爬行时，只能从一个格爬到相邻的大号格子中。例如，从 1 号格子可以爬到 2 号或者 3 号格子，从 2 号则可以爬到 3 号或者 4 号格子。

 

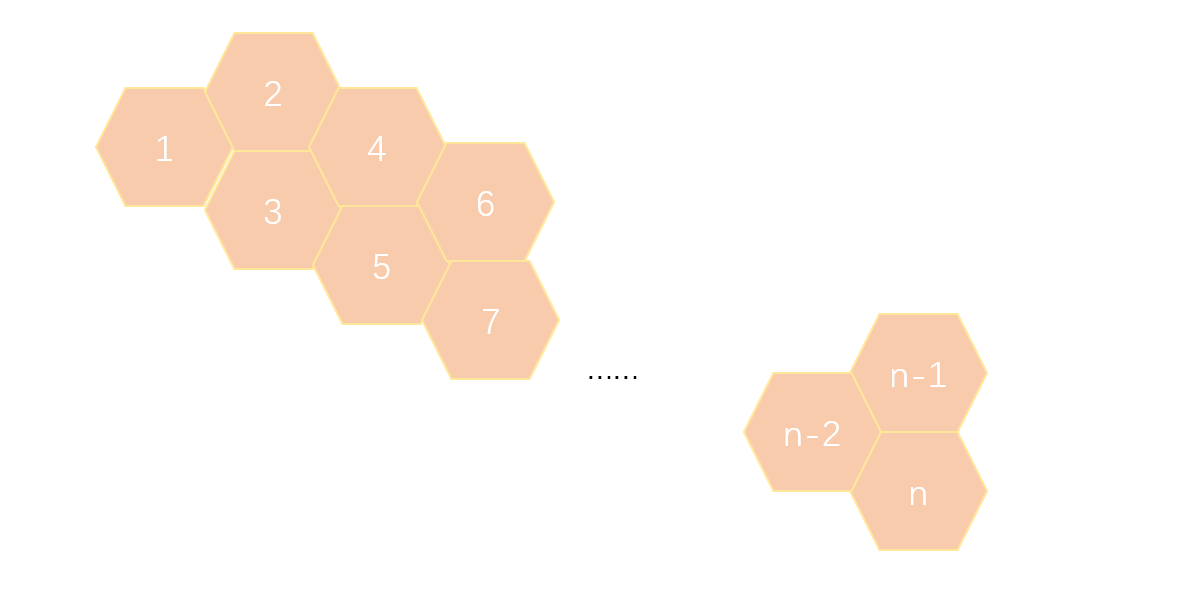
    请问从一个格子 a 爬到一个格子 b 一共有多少种可行的路线。

输入：

    分别是起始点 a 和终止点 b 的编号。（ a 和 b 在 1~100 之间，且 a<b 。）

输出：

    方案数量。

	测试输入	期待的输出	时间限制	内存限制	额外进程
测试用例 1	以文本方式显示 1 4↵	以文本方式显示 3↵	1秒	64M	0
测试用例 2	以文本方式显示 1 5↵	以文本方式显示 5↵	1秒	64M	0
测试用例 3	以文本方式显示 1 50↵	以文本方式显示 12586269025↵	1秒	64M	0
测试用例 4	以文本方式显示 2 50↵	以文本方式显示 7778742049↵	1秒	64M	0
测试用例 7	以文本方式显示 1 100↵	以文本方式显示 354224848179261915075↵	1秒	64M	0

 

【分析】：

本质上是一道高中排列组合数学题
爬楼梯，可以一次爬一格，也可以一次怕两格，到顶层问有多少中爬法。也就是一个斐波那契数列
大意了，它的数字实在是太大了，要用特殊的手段处理大数
之前做过一道题，处理大数的加减，直接copy代码

【代码】

#include <stdio.h>
void intcpy(int arr1[], const int arr2[]);
void Fibonacci(int n);
int main(void){
	/*本质上是一道高中排列组合数学题
	* 爬楼梯，可以一次爬一格，也可以一次怕两格，到顶层问有多少中爬法。也就是一个斐波那契数列,f3=f2+f1
	* 大意了，它的数字实在是太大了，要用特殊的手段处理大数
	* 哦，需要打印的是Fibonacci数列的第(b-a+1)项
	*/
	int a, b;
	scanf("%d %d", &a, &b);
	Fibonacci(b - a);
	return 0;
}

void Fibonacci(int n)
{
	 int f1[100] = {1}, f2[100] = {1}, f3[100] = {0};
	//100个字符对于斐波那契数列的前已经足够了	
	 if (n == 1) printf("%d\n", 1);
	 else {
		 for (int i = 1; i < n; i++) {
			 for (int j = 0; j < 99; j++) {
				 f3[j] += f1[j] + f2[j];
				 f3[j + 1] = f3[j] / 10;
				 f3[j] %= 10;
			 }
			 intcpy(f1, f2);
			 intcpy(f2, f3);
			 if (i != n - 1)for (int k = 0; k < 100; k++) f3[k] = 0;
		 }
		 int end = 0;
		 for (int i = 99; i >= 0; i--)
			 if (f3[i] != 0) {
				 end = i; break;
			 }
		 for (int i = end; i >= 0; i--) printf("%d", f3[i]);
		 putchar('\n');
	 }
}
void intcpy(int arr1[], const int arr2[])
{
	for (int i = 0; i < 100; i++) arr1[i] = arr2[i];
}