三种背包问题(01背包、完全背包、多重背包)【动态规划】
转载自 【动态规划】三种背包问题(01背包、完全背包、多重背包)
01背包
问题描述
给定n个物体(它们的重量为:w1,w2,......,wn,价值为:v1,v2,......,vn) 和 一个承受重量为W的背包,
问怎么选取这些物体,放在背包中(不超过背包的承重),让所取的子集达到最大价值。
实现思路
穷举法
只要给出n个物体的所有组合(子集),分别各个子集的总价值,去掉那些总重量超过背包承重W的子集之后,
对剩下的子集中找到总价值最大的那一个,就是我们想要的结果了。
由于n各物体的有2n个子集,所以上面的做法的时间复杂度将是O(2n),除非n很小,否则时间性能消耗非常严重。
01背包算法基本实现
/**
* @Author hwj
* @Date 2020/8/16 22:09
* @Desc: 给定n个物体(它们的重量为:w1,w2,......,wn,价值为:v1,v2,......,vn) 和 一个承受重量为W的背包,
* 问怎么选取这些物体,放在背包中(不超过背包的承重),让所取的子集达到最大价值。
**/
public class package01 {
public static void main(String[] args){
//w[]:物品重量,v[]:物品价值,m:背包承重,n:物品个数,maxValue[][]:状态
int[] w = {0, 10, 3, 4, 5}; //第一个数为0,是为了让输出时,i表示有i个物品
int[] v = {0, 3, 4, 6, 7};
int m = 10;
int n = 4;
int[][] maxValue = new int[5][16];
// 01背包算法
for (int i=1; i<=n; i++) { //第一个物体 是 第1行
for (int j=0; j<=m; j++) {
// 在背包承重为 j 时,所能达到的最大价值
if (i > 0) {
// maxValue[i-1][j]:最大价值为 在承重为 j 的情况下,不放入第i物体的最大价值
maxValue[i][j] = maxValue[i-1][j];
// 当承重开始超过第i个,比较 不放入i物体 与 放入 i 物体相比
if (j >= w[i]) {
maxValue[i][j] = max(maxValue[i][j], maxValue[i-1][j-w[i]] + v[i]);
//注:maxValue[i][j]其实就是maxValue[i-1][j] 因为上面的赋值
}
} else { //初始化,只考虑一个物体
if (j >= w[1]) {
maxValue[1][j] = v[1];
}
}
}
}
System.out.println("4个物品在背包承重为10的情况下的组合的最大价值为:"+maxValue[n][m]);
System.out.println();
// 打印背包的不同承重量
System.out.print(" " + "\t");
for (int i=0; i<=m; i++) {
System.out.print(i + "\t");
}
System.out.println();
// 打印01背包算法 得到的状态矩阵值
for (int i=1; i<=n; i++) {
System.out.print("i="+ i +"\t");
for (int j=0; j<=m; j++) {
System.out.print(maxValue[i][j]+"\t");
}
System.out.println();
}
}
public static int max(int a, int b) {
if (a > b) {
return a;
}
return b;
}
}
一维数组实现 01背包
01背包还可以用一维数组实现,只不过此时的递推式 & 初始条件就需要做些改变了。
要想用一维数组存放所有状态,也就是让该数组某个时间是第 i-1 层的状态,而过一段时间之后则成为第 i 层的状态。
覆盖的过程中,应该采用从后到前的顺序遍历。首先,改写maxValue[ W ]的值。
这是由于计算 i层 的maxValue[ W-1 ] 不需要用到 i-1 的maxValue[ W ]状态,所以,maxValue[ W ]的改动不影响maxValue[ W-1 ]的计算。
以此类推,就可以在原来的数组上面不断覆盖最新一层的状态值了。
/**
* @Author hwj
* @Date 2020/8/16 22:09
* @Desc: 给定n个物体(它们的重量为:w1,w2,......,wn,价值为:v1,v2,......,vn) 和 一个承受重量为W的背包,
* 问怎么选取这些物体,放在背包中(不超过背包的承重),让所取的子集达到最大价值。
**/
public class package01 {
public static void main(String[] args){
//w[]:物品重量,v[]:物品价值,m:背包承重,n:物品个数,maxValue[][]:状态
int[] w = {0, 10, 3, 4, 5}; //第一个数为0,是为了让输出时,i表示有i个物品
int[] v = {0, 3, 4, 6, 7};
int m = 10;
int n = 4;
int[] maxValue = new int[16];
// 01背包算法
for (int i=1; i<=n; i++) {
for (int j=m; j>=w[i]; j--) {
maxValue[j] = max(maxValue[j], maxValue[j-w[i]] + v[i]);
}
//验证 结果和二维实现的输出结果完全一样
//for (int k=0; k<=m; k++) {
// System.out.print(maxValue[k] + "\t");
//}
//System.out.println();
}
System.out.println("4个物品在背包承重为10的情况下的组合的最大价值为:"+maxValue[m]);
System.out.println();
// 打印背包的不同承重量
System.out.print(" " + "\t");
for (int i=0; i<=m; i++) {
System.out.print(i + "\t");
}
System.out.println();
// 打印01背包算法 得到的状态矩阵值
for (int i=1; i<=n; i++) {
System.out.print("i="+ i +"\t");
for (int j=0; j<=m; j++) {
System.out.print(maxValue[j]+"\t");
}
System.out.println();
}
}
public static int max(int a, int b) {
if (a > b) {
return a;
}
return b;
}
}
完全背包
问题描述
完全背包是在01背包的基础上加了个条件——这n种物品都有无限的数量可以取,问怎样拿才可以实现价值最大化。
问题分析
虽然题意中每种有无限件,但这里有个隐藏条件:背包承重量的固定性导致每种最多只能取某个值,再多就放不下了,这个值就是W / wi。也就是说,
对于第 i 种物品,它可以取0,1,2,......,W / wi(向下取整)件。而在01背包中,对于第 i 种物品,只能取0,1件。我们可以看到,
01背包其实就是完全背包的一个特例。所以我们可以用类似01背包的思路写出完全背包的基本算法。
具体实现代码
二维数组实现
/**
* @Author hwj
* @Date 2020/8/16 23:30
* @Desc:
**/
public class PackageComplete {
public static void main(String[] args) {
int[] w = {0,10, 3, 4, 5};
int[] v = {0,3, 4, 6, 7};
int m = 10;
int n = 4;
int[][] maxValue = new int[5][16];
for (int i=1; i<=n; i++) {
for (int j=0; j<=m; j++) {
if (i > 1) {
maxValue[i][j] = maxValue[i-1][j];
//if (j >= v[i]) {
// maxValue[i][j] = max(maxValue[i][j], maxValue[i-1][j-v[i]] + w[i]);
//}
if (j/w[i] >= 1) {
int maxTmp = 0;
// 对于i个物品,进行j/w[i]次比较得到最大值;而01背包中只需要进行1次比较
for (int k=1; k<=j/w[i]; k++) {
if (maxValue[i-1][j-k*w[i]] + k*v[i] > maxTmp) {
maxTmp = maxValue[i-1][j-k*w[i]] + k*v[i];
}
}
maxValue[i][j] = max(maxValue[i][j], maxTmp);
}
} else {
//if (j >= v[0]) {
// maxValue[0][j] = w[0];
//}
if (j/w[1] >= 1) {
maxValue[1][j] = j/w[1] * v[1];
}
}
}
}
System.out.println("4个物品在背包承重为10的情况下的组合的最大价值为:"+maxValue[n][m]);
System.out.println();
// 打印背包的不同承重量
System.out.print(" " + "\t");
for (int i=0; i<=m; i++) {
System.out.print(i + "\t");
}
System.out.println();
// 打印01背包算法 得到的状态矩阵值
for (int i=1; i<=n; i++) {
System.out.print("i="+ i +"\t");
for (int j=0; j<=m; j++) {
System.out.print(maxValue[i][j]+"\t");
}
System.out.println();
}
}
public static int max(int a, int b) {
if (a > b) {
return a;
}
return b;
}
}
一维数组实现
/**
* @Author hwj
* @Date 2020/8/16 23:30
* @Desc:
**/
public class PackageComplete {
public static void main(String[] args) {
int[] w = {0,10, 3, 4, 5};
int[] v = {0,3, 4, 6, 7};
int m = 10;
int n = 4;
int[] maxValue = new int[16];
for (int i=1; i<=n; i++) {
//for (int j=m; j>=w[i]; j--) {
// 正序遍历; 01背包是逆序遍历
for (int j=w[i]; j<=m; j++) {
maxValue[j] = max(maxValue[j], maxValue[j-w[i]] + v[i]);
}
//验证 结果和二维实现的输出结果完全一样
//for (int k=0; k<=m; k++) {
// System.out.print(maxValue[k] + "\t");
//}
//System.out.println();
}
System.out.println("4个物品在背包承重为10的情况下的组合的最大价值为:"+maxValue[m]);
System.out.println();
for (int i=0; i<=m; i++) {
System.out.print(maxValue[i] + "\t");
}
}
public static int max(int a, int b) {
if (a > b) {
return a;
}
return b;
}
}
多重背包
问题描述
多重背包是在01背包的基础上,加了个条件:第 i 件物品有ni件。
问题分析
我们考虑一下,如果所有ni都满足ni ≥ W / wi,那不就变成完全背包的问题了么。可见,完全背包的基本实现思路也可以应用到多重背包的基本实现。对于多重背包的基本实现,与完全背包是基本一样的,不同就在于物品的个数上界不再是v/c[i]而是n[i]与v/c[i]中较小的那个。所以我们要在完全背包的基本实现之上,再考虑这个上界问题。
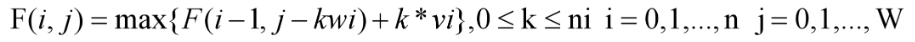
代码实现如下所示,代码与完全背包的区别除了多了个表示物品个数的数组n[ ]之外,只在内循环的控制条件那里。
## 二维数组实现
/**
* @Author hwj
* @Date 2020/8/16 23:40
* @Desc:
**/
public class MultiplePackage {
public static void main(String[] args) {
int[] w = {0,10, 3, 4, 5};
int[] v = {0,3, 4, 6, 7};
//第i个物品对应的个数
int[] mount = {0,5,1,2,1};
int m = 10;
int n = 4;
int[][] maxValue = new int[5][16];
for (int i=1; i<=n; i++) {
for (int j=0; j<=m; j++) {
if (i > 1) {
maxValue[i][j] = maxValue[i-1][j];
if (j/w[i] >= 1) {
int maxTmp = 0;
//for (int k=1; k<=j/w[i]; k++) {
//多重背包与完全背包的区别只在内循环这里
for (int k=1; k<=j/w[i] && k<=mount[i]; k++) {
if (maxValue[i-1][j-k*w[i]] + k*v[i] > maxTmp) {
maxTmp = maxValue[i-1][j-k*w[i]] + k*v[i];
}
}
maxValue[i][j] = max(maxValue[i][j], maxTmp);
}
} else {
if (j/w[1] >= 1) {
maxValue[1][j] = j/w[1] * v[1];
}
}
}
}
System.out.println("4个物品在背包承重为10的情况下的组合的最大价值为:"+maxValue[n][m]);
System.out.println();
// 打印背包的不同承重量
System.out.print(" " + "\t");
for (int i=0; i<=m; i++) {
System.out.print(i + "\t");
}
System.out.println();
// 打印01背包算法 得到的状态矩阵值
for (int i=1; i<=n; i++) {
System.out.print("i="+ i +"\t");
for (int j=0; j<=m; j++) {
System.out.print(maxValue[i][j]+"\t");
}
System.out.println();
}
}
public static int max(int a, int b) {
if (a > b) {
return a;
}
return b;
}
}
谋定而后动,知止而有得



 浙公网安备 33010602011771号
浙公网安备 33010602011771号