堆

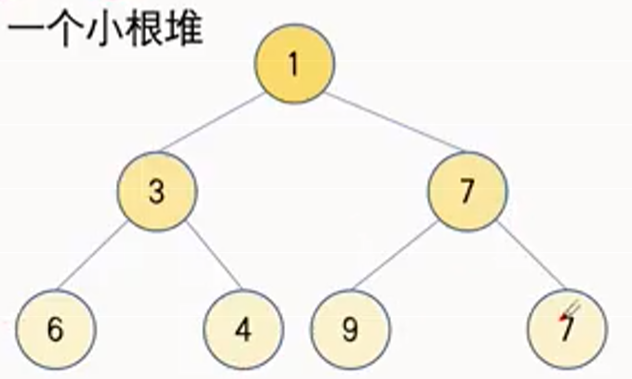
1. 定义

• 根其实就是一个完全二叉树
• 堆中某个结点的值总是不大于或不小于其父节点的值
• 堆中的根节点的值是整个堆的最大值或最小值

对于数组[t]位置：

• 左二子为[2t]
• 右儿子为[2t+1]
• 父节点为[t/2]

大根堆：父节点的值>=两个子节点的值
小根堆：父节点的值<=两个子节点的值

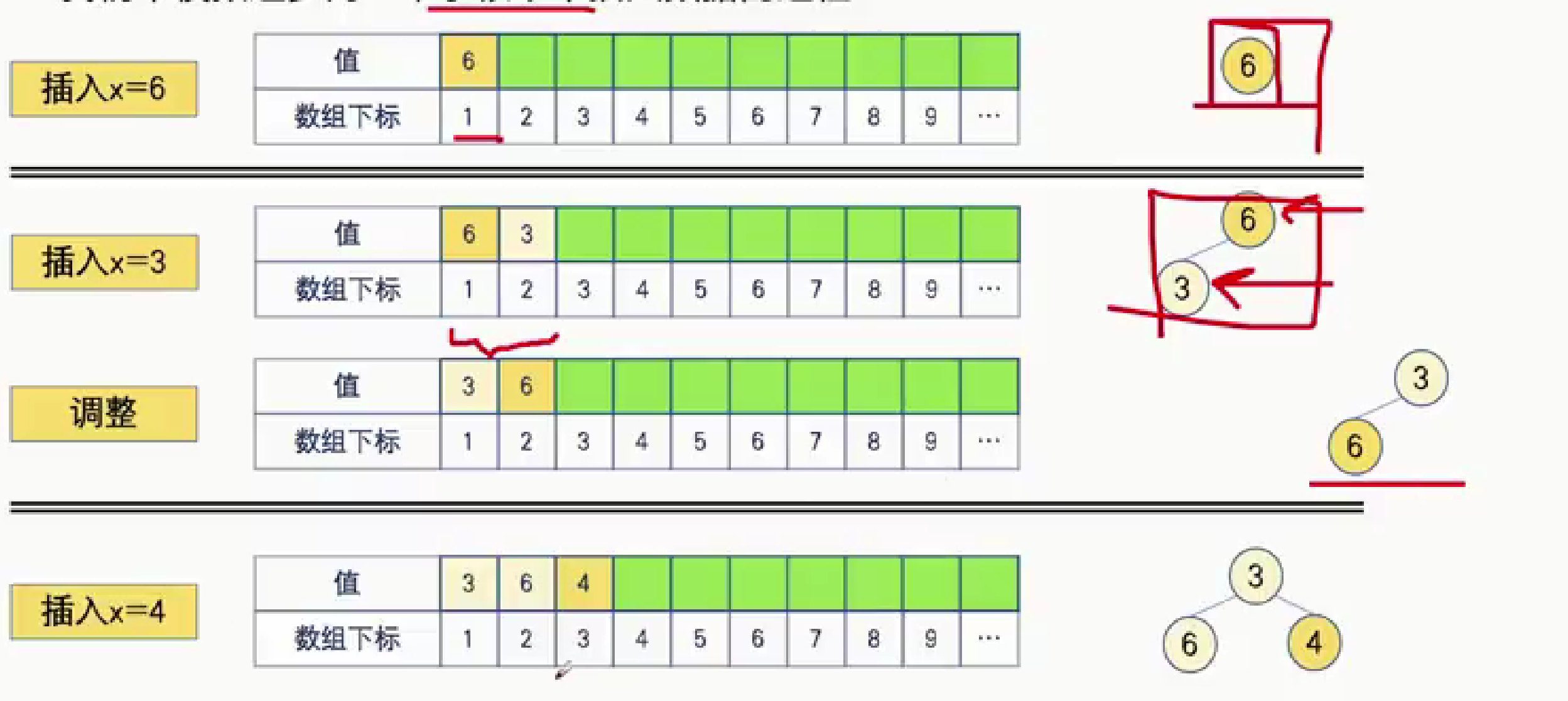
2. 插入数据

拿小根堆举例，模拟一个个插入数据的过程

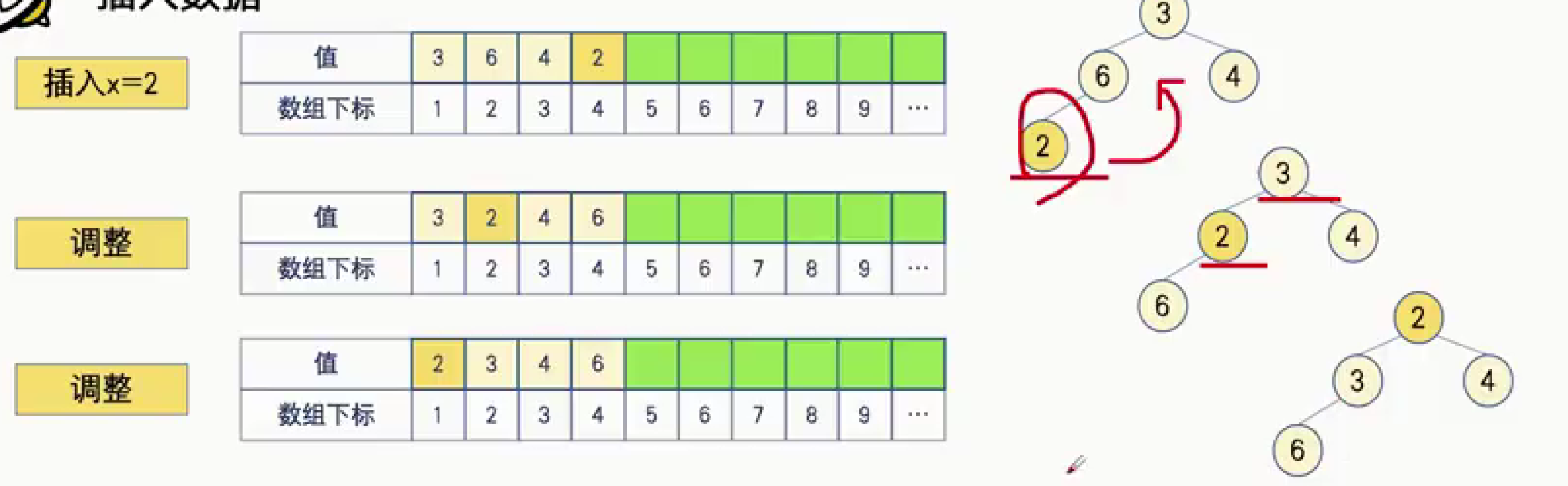
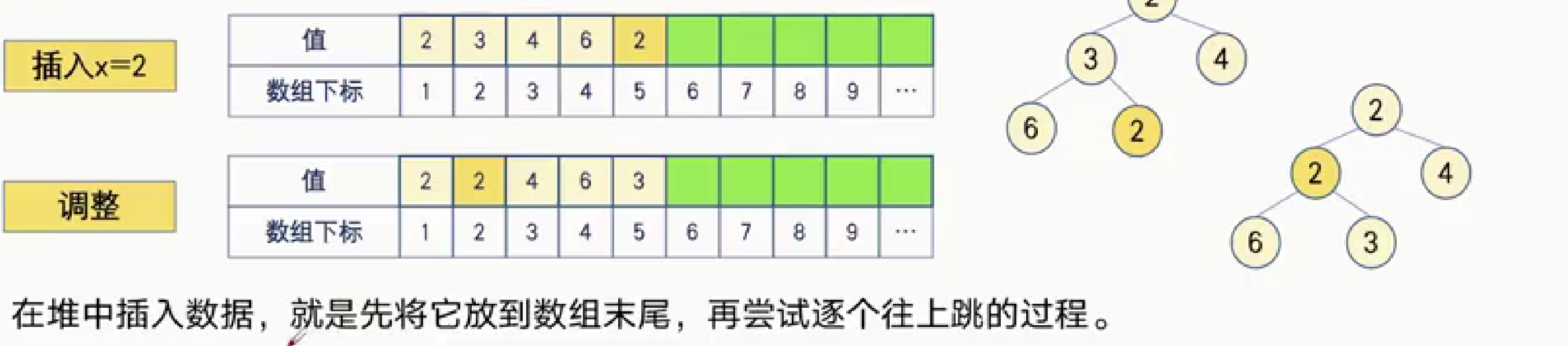
3. 删除数据

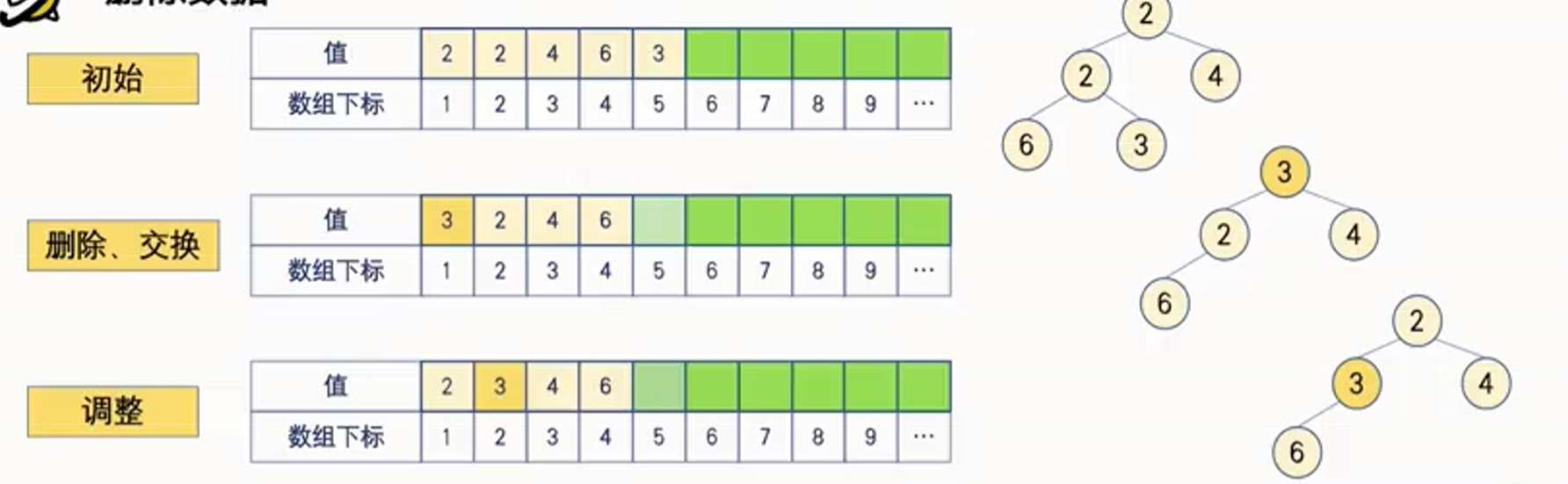
我们可以将堆尾元素放到删除的元素的位置然后进行逐步上移(拿小根堆来说就是如果这个值小于父节点的值就将这个值与父节点交换)再进行逐步下移（拿小根堆来说就是将这个值与儿子节点中的最小者交换）

4. 例题

1. 堆排序

# include<bits/stdc++.h>

using namespace std;

const int N = 1e5+10;
int a[N];
int len;

void up(int x)
{
	while(x/2)
	{
		if(a[x/2]>a[x])
		{
			swap(a[x/2],a[x]);
			x/=2;
		}
		else break;
	}	
}

void down(int x)
{
	while(x*2<=len)
	{
		int k = x*2; 
		if(x*2+1<=len && a[x*2+1]<a[k]) k = x*2+1;
		if(a[k]<a[x])
		{
			swap(a[k],a[x]);x = k;
		}
		else break;
	}
}

int main()
{
	int n;cin>>n;
	for(int i=1;i<=n;i++)
	{
		int x;cin>>x;
		a[++len] = x;
		up(len);
	}

	for(int i=1;i<=n;i++)
	{
		cout<<a[1]<<" ";
		swap(a[1],a[len--]);
		up(1);down(1);
	}
	return 0;
}

2. 动态中位数 https://www.acwing.com/problem/content/108/

# include<bits/stdc++.h>

using namespace std;

int main()
{
    int t;cin>>t;
    while(t--)
    {
        priority_queue<int> a; //大根堆a存所有a.top()小的数
        priority_queue<int,vector<int>,greater<int>> b; //小根堆b存所有比a.top()大的数，b.top()是最小的比a.top()大的数
        int id,n;cin>>id>>n;
        cout<<id<<" "<<(n+1)/2<<endl;
        int l;cin>>l;
        cout<<l<<" ";
        int cnt = 1;
        a.push(l);
        for(int i=1;i<=n/2;i++)
        {
            int x,y;cin>>x>>y;
            int z = a.top();
            
            if(x>z) b.push(x);
            else a.push(x);
            if(y>z) b.push(y);
            else a.push(y);
            
            //确保a.size()一直比b.size()大1，这样a.top()就是中位数
            if(b.size()>a.size()) 
            {
                a.push(b.top());b.pop();
            }
            else if(a.size()-b.size()>1) 
            {
                b.push(a.top());a.pop();
            }
            cout<<a.top()<<" ";
            cnt++;
            if(cnt%10 == 0 && i<n/2) cout<<endl;
        }
        cout<<endl;
    }
    return 0;
}