命题

1. 命题的概念

命题是指具有唯一真值的陈述句

例题

1. \(1+101 = 110\)
   
   这个式子在十进制是假的，在二进制下是真的，不符合命题有唯一真值

2. 全体立正!
   
   祈使句,不符合命题是陈述句

3. 别的星球有生物。
   
   虽然我们并不知道这句话是真是假，但它的真值是客观存在的，具有唯一真值。不以我们的意志为转移。所以是命题

4. 明天是否下雨?
   
   疑问句。与2同理

5. 我正在说谎
   
   悖论。若此句为假，则可以推出真。若此句为真，则可以推出假。不是命题。

原子命题和复合命题

• 原子命题
  如果一陈述句再也不能分解成更为简单的语句，由他构成的命题称为原子命题，是命题逻辑的基本单位

• 复合命题
  由原子命题、命题联结词和圆括号组成

2. 命题联结词

否定联结词 ： \(\urcorner\)
和取联结词 ： \(\bigwedge\) 相当于数字逻辑里的与
析取联结词 ： \(\bigvee\) 相当于数字逻辑里的或

3. 条件联结词

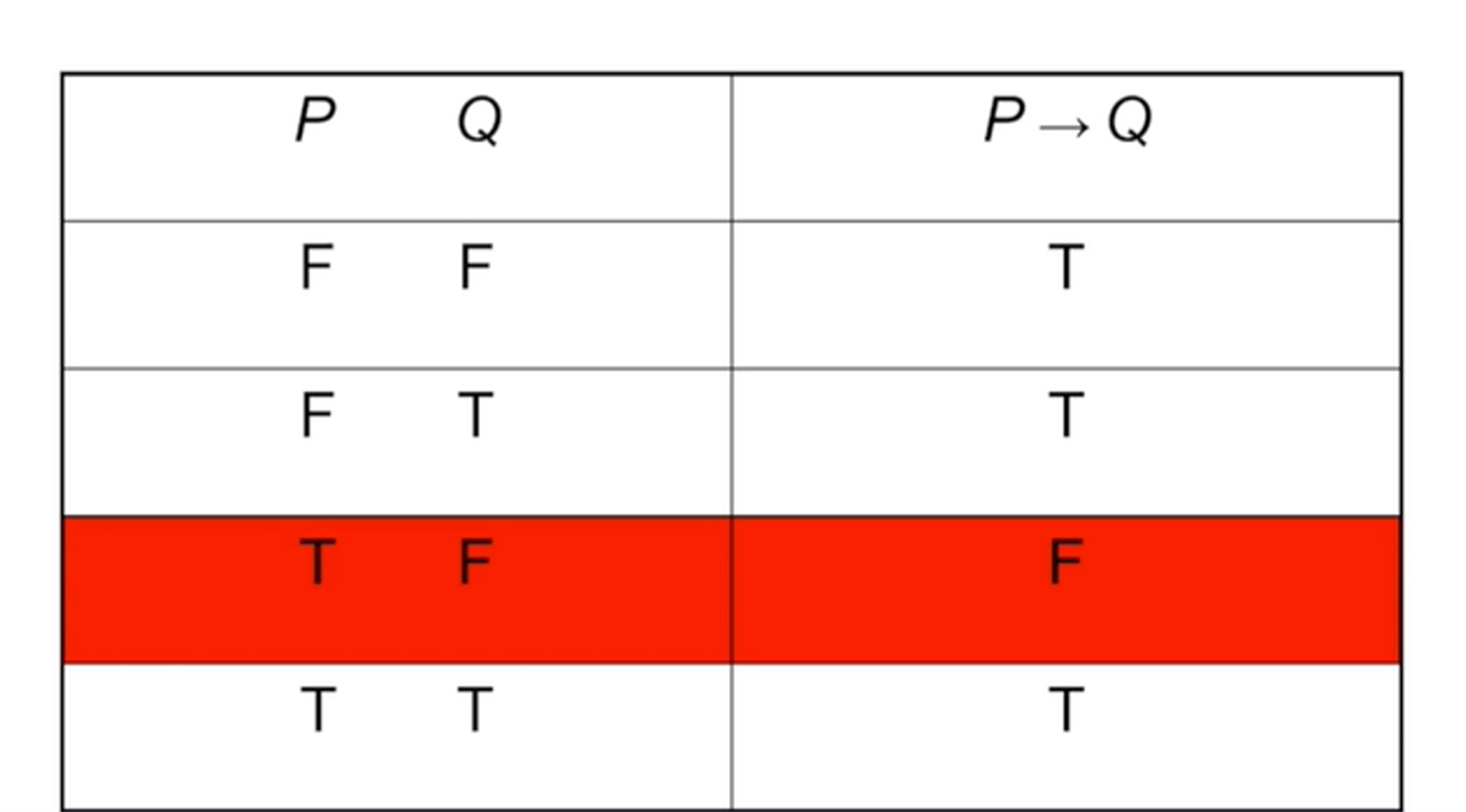
• \(p \rightarrow q\)
  
  可以表示若p则q。小范围可推大范围，0为小范围，1为大范围。所以只有当p为真，q为假时，该式为假，其他情况为真
  

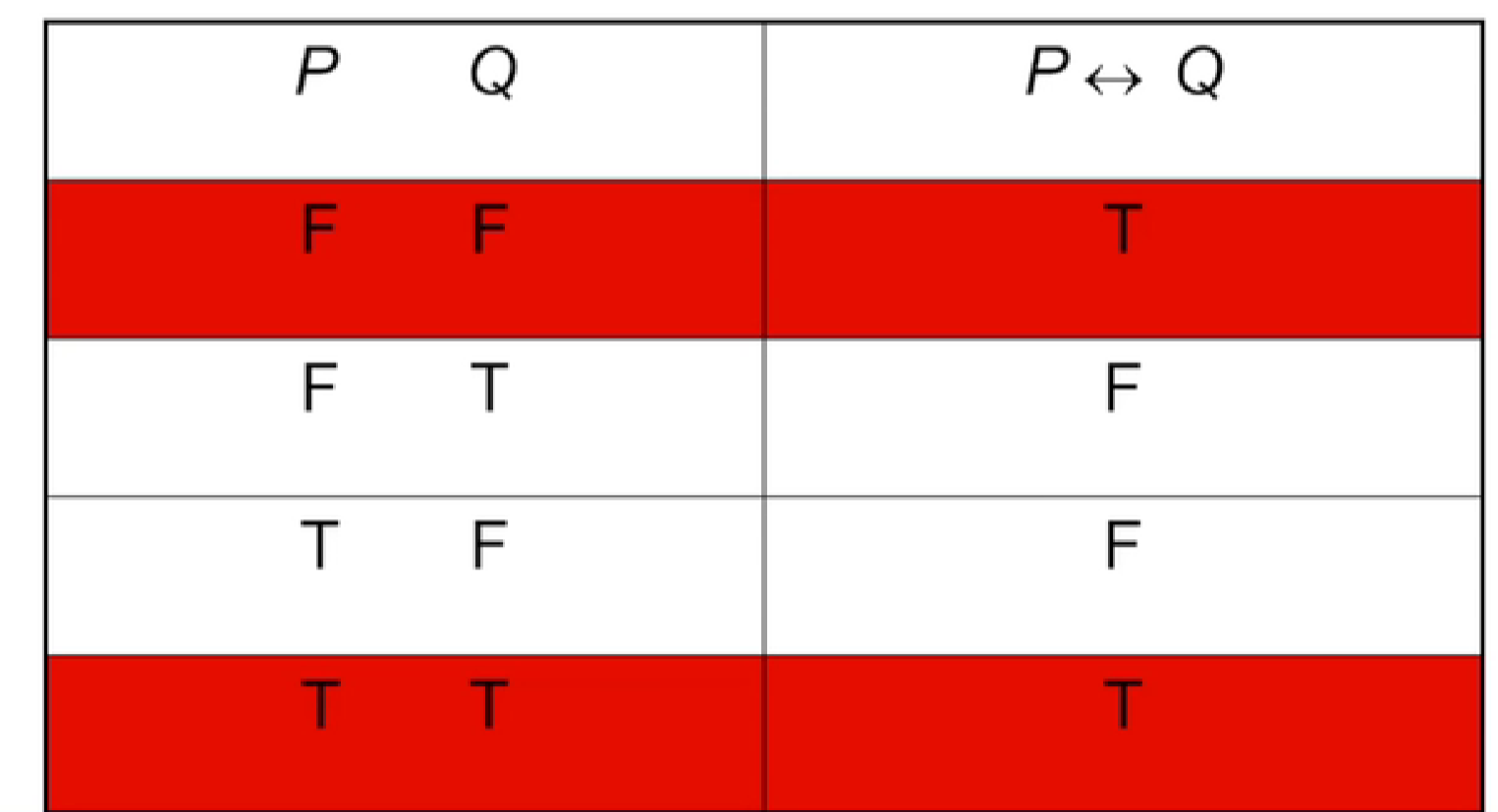
• p\(\leftrightarrow\)q
  
  可以表示为p当且仅当q
  

4. 命题的翻译和符号化

5. 等价关系

对于两个命题公式A和B，A和B的真值都相同则\(A\Leftrightarrow B\)
$p\rightarrow q \Leftrightarrow \urcorner p \bigvee q $

$p \leftrightarrow q \Leftrightarrow (p\rightarrow q)\bigwedge(q\rightarrow p) $

6. 重言式与蕴含式

• 重言式
  永真式，真值永远为T，比如\(\urcorner p \bigvee p\)

• 矛盾式
  永假式，真值永远为F,比如\(\urcorner p \bigwedge p\)

• 可满足式
  当某个命题不是矛盾式，则称之为可满足式

• 蕴含式
  当且仅当\(P\rightarrow Q\)是重言式时，我们称P蕴含Q，记作\(P\Rightarrow Q\)

要证明\(P\Rightarrow Q\),只需证明\(\urcorner Q \Rightarrow \urcorner P\)

或者证明\(P \rightarrow Q\)是重言式

7. 其他联结词

• 与非： \(P \uparrow Q \Leftrightarrow \urcorner(p\bigwedge Q)\)
• 或非： \(P \downarrow Q \Leftrightarrow \urcorner(P\bigvee Q)\)

8. 全功能联结词组

一个联结词集合，用其中联结词足以把一切命题公式表达出来，则这个联结词集合为全功能的

9. 对偶式

10. 范式

极小项

在n个变元的基本积中，每个边元和它的否定不同时存在且两者之一必出现一次且仅出现一次叫做极小项

极大项

在n个变元基本和中......(其他与极小项一样)

合取范式

主合取范式

由极大项之积组成的公式

析取范式

主析取范式

由极小项之和组成的公式

11. 推理理论