第二章 信息的表示和处理

一. 信息存储

1. 概念先行

位：
bit:音译为“比特”，简称“b”，指二进制位，由0，1组成

字节：
Byte：译为“字节”，简称“B”,在它之后还有Kb,Mb,GB
是计算机系统中最小的存储单位。一个字节8位

字：

32位计算机 ： 字 = 4字节 = 32位
64位计算机 ： 字 = 8字节 = 64位

字长：

字长就是字的位数
字长 = 运算器位数 = 通用寄存器位数 = pc宽度
通俗点说就是字长和你可以运算的位数以及寻址的位数是统一的

字长是向后兼容的，64位机器可以运行32位机器编译的程序。
比如当程序prog.c用如下伪指令编译

linux>gcc -m32 prog.c

该程序可以在32位或64位机器上正确运行

但当程序用下述指令编译

linux>gcc -m64 prog.c

该程序只能在64位机器上运行

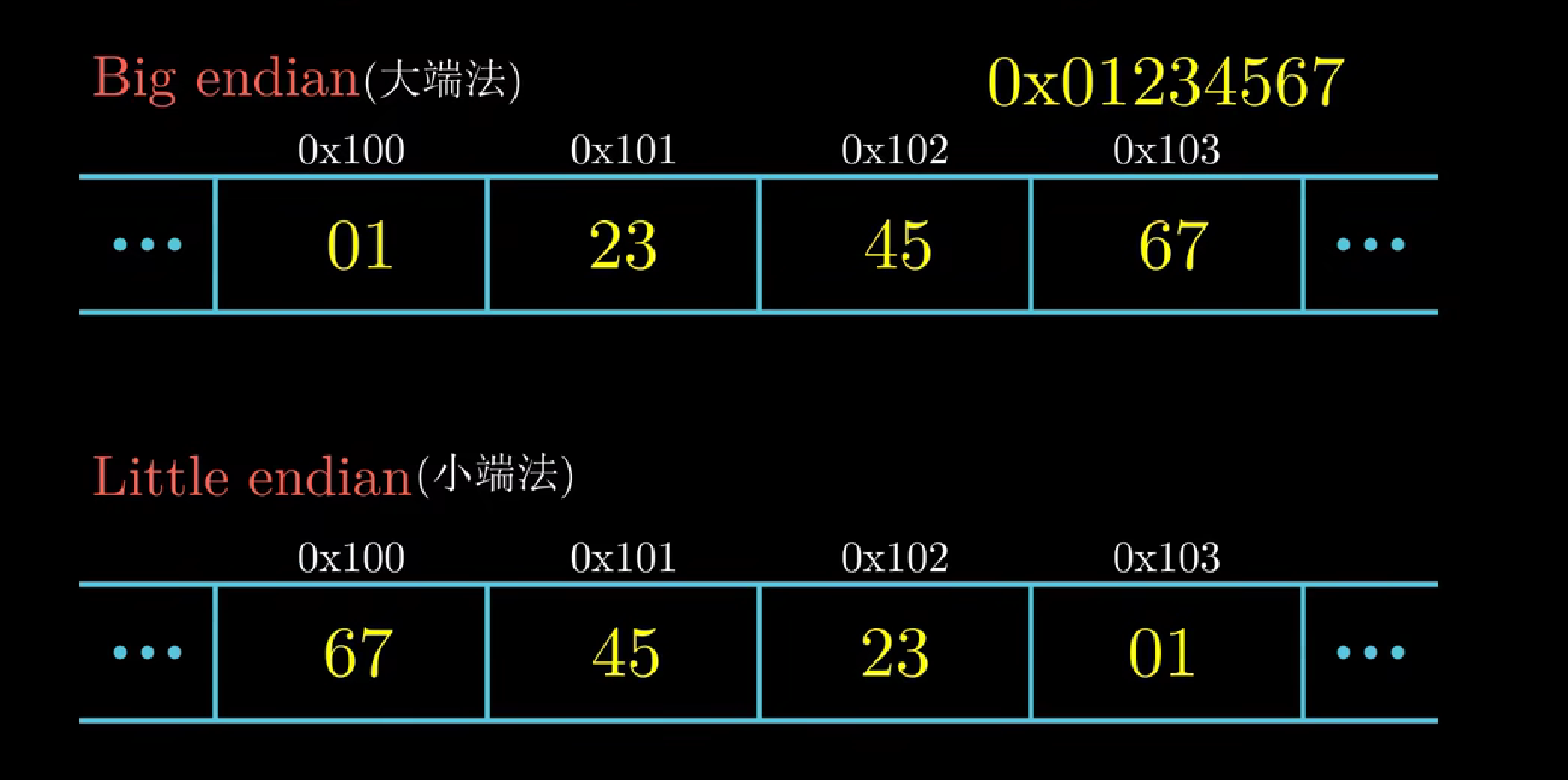
2. 寻址和字节顺序

多字节对象被存在连续的字节序列，对象的地址为最小的地址

假设一个int类型的变量x的4个字节被存储在内存0x100、0x101、0x102和0x103四个位置，那么对象的地址就是四个地址里面最小的0x100

一个地址表示一个字节，8位二进制（正如前面所说的字节是计算机系统中最小的存储单位）

对于int类型变量x，位于地址0x100处，它的十六进制值为0x01234567,字节的存储顺序根据机器类型有两种规则

3.位运算

• 掩码
  用一串二进制数字（掩码）去操作另一串二进制数字

  比如我们想得到x = 0x89ABCDEF的最低有效字节组成的值，那么我们可以用掩码0xFF&x，其表达式将得到0x000000EF

• 移位

  1. 左移：末尾补0，相当于原数*2
  2. 逻辑右移 ： 前面补0，相当于原数/2
  3. 算数右移：前面补符号位，也相当于原数/2

对于几乎所有编译器/机器组合都对有符号数使用算术右移，无符号数使用逻辑右移

但其实我们完全可以直接把右移当做算术右移，反正最后补符号位的话无符号数也是补的0

• 关于移位的细节
  要注意的一点是对于负数的移位是在补码下进行的，下面是一个对于-10右移一位的代码

# include<bits/stdc++.h>

using namespace std;

void print_binary(int x)
{
	int cnt = 0;
	vector<int> ans;
	while(x) 
	{
		cnt++;
		ans.push_back( (int)(x&1) ) ;
		x>>=1;
		if(cnt == 32) break;//因为负数右移一直添1所以要特判位数来break，防止死循环
	}
	for(int i=31;i>=0;i--) cout<<ans[i];
	cout<<endl;
}
int main()
{
	int x = -10;
	print_binary(x);
	x>>=1;
	print_binary(x);
	return 0;
}

输出结果为：

11111111111111111111111111110110
11111111111111111111111111111011

二. 整数表示

1. 补码编码

之前理解补码的时候单纯的觉得负数的补码就是原码符号位不变其他取反+1
负数的原码就是符号位取1，然后其他位凑出该负数的绝对值

比如对于 int类型 -10:

原码100000000....1010
补码111111111....0110

但其实补码的符号位也可以理解为带位权的，位权为\(-2^{w-1}\) , w为补码位数

2. 有符号数和无符号数之间转换

对于向量\(x = [x_{w-1},x_{w-2},x_{w-3},...,x_0]\)

\[\begin{align*} &有符号数：x_{w-1}*-2^{w-1}+x_{w-2}*2^{w-2}+...+x_0*2^0\\ &无符号数：x_{w-1}*2^{w-1}+x_{w-2}*2^{w-2}+...+x_0*2^0\\ &无符号数-有符号数 = x_{w-1}*2^{w-1} - x_{w-1}*-2^{w-1} = x_{w-1}*2^w \end{align*} \]

• 有符号数转无符号数

\[无符号数 = 有符号数+ x_{w-1}*2^w \]

那么对于二进制数的最高位\(x_{w-1}\):
\(x_{w-1}=0(即有符号数>=0)\) : 无符号数 = 有符号数
\(x_{w-1}=1(即有符号数<0)\) : 无符号数 = 有符号数+\(2^w\)

\[无符号数 = \begin{cases} 有符号数+2^w,\,\,x<0\\ 有符号数,\,\,x>=0 \end{cases} \]

• 无符号数转有符号数

\[有符号数 = 无符号数-x_{w-1}*2^w \]

那么对于二进制数的最高位\(x_{w-1}\):
\(x_{w-1}=0(即无符号数<=有符号数的最大值)\) : 有符号数 = 无符号数
\(x_{w-1}=1(即无符号数>有符号数的最大值)\) : 有符号数 = 无符号数-\(2^w\)

3. 扩展一个数字的位表示（小数字类型转换为大数字类型）

• 将一个无符号数转换为一个更大的数据类型

  只需要在高位补0即可
  比如对unsigned char 类型的a向量\([x_7,x_6,...,x_0]\)
  转换为unsigned short类型的b向量
  \(b=[0,0,0,0,0,0,0,0,x_7,x_6,...,x_0]\)

• 将一个有符号数转换为一个更大的数据类型

  需要在扩展的位上补符号位
  比如对char 类型的a向量\([x_7,x_6,...,x_0]\)
  转换为short类型的b向量
  \(b=[x_7,x_7,x_7,x_7,x_7,x_7,x_7,x_7,x_7,x_6,...,x_0]\)

• 对于有符号数为负数时扩展位全部补1的解释

  假如我们可以证明每次符号位扩展1位，都可以保持数值不变。那么扩展k位不过是进行k次扩展一位，同样也可以保持数值不变

\[\begin{align*} 设t&=x_{w-2}*2^{w-2}+...+x_0*2^0\\ \\ 原有符号数&=x_{w-1}*-2^{w-1}+t\\ \\ 扩展一位&=x_{w-1}*-2^{w}+x_{w-1}*2^{w-1}+t\\ &=x_{w-1}*-2^{w-1}\\ &=原有符号数 \end{align*} \]

所以每次符号位扩展一位都可以保持数值不变，那么扩展k位就是扩展k次符号位

4. 截断数字（大数字类型转换为小数字类型）

• 截断无符号数

令\(x = [x_{w-1},x_{w-2},...,x_{0}]\)

\(x'\)是将其截断为k位的结果

\(x'= [{x_{k-1},x_{k-2},...,x_0}]\)

\(x'=x\) mod \(2^k\)、

• 截断有符号数

补码截断也具有相似的属性，只不过要将最高位转换为符号位

我们可以将整个过程分成两步

1. 按照无符号数的方式截断
2. 将第一步得到的无符号数转换成有符号数

经过这两步我们就可以得到截断之后有符号数的值

三. 整数运算

1. 无符号加法

定义无符号整数x，y。

x+y的结果是x+y截断为w位得到的结果。

unsigned char a = 255,b = 1
unsigned char ans = a+b;
printf("%d",ans);

最后结果是0而不是我们直觉上的256


unsigned char 一共有8位

\[\begin{align*} \ a &= 11111111\\ b &= 00000001\\ ans&=100000000 \end{align*} \]

因为无符号数加法的结果是截断为w为得到的结果，所以最高位1会被舍弃，ans被截断为00000000,也就是0

所以一旦溢出，我们有：

\[x+y得到的结果 = x+y-2^w \]

同时，因为我们的程序运行时时不会告诉你是否溢出的，那么我们可不可以自己写一个程序来判断是否溢出呢

bool uadd_ok(unsigned x,unsigned y)
{
	unsigned ans = x+y;
	return ans>=x; //如果x+y的值大于等于x则无溢出否则溢出
}

因为一旦溢出，\(ans = x+y-2^w\)
又因为\(x<2^w\) && \(y<2^w\),所以\(x-2^w<0\) && \(y-2^w<0\)

所以\(ans<x\) && \(ans<y\)

2. 有符号加法

和无符号数加法一样，有符号数一样是截断w位后得到的结果

• 正溢出

char a = 127,b = 1;
char ans = a+b;
printf("%d",ans)

对于上述代码，我们希望得到的结果是128，但是最后的结果是-128

a = 01111111
b = 00000001
ans = 10000000

因为有符号的运算是在补码上进行的，所以1000000的值为0

• 负溢出

char a = -128,b = -1;
char ans = a+b;
printf("%d",ans);

a = 10000000
b = 11111111

ans = 1 01111111 最高位1溢出舍去，结果是01111111 = 127

3. 减法运算

加法逆元：如果\(x+x'=0\)，那么\(x'\)是\(x\)的加法逆元

对于\(x-y\)，其实就是\(x+y'\)，然后也遵循截断w位这个规则

这里要注意的就是补码的最小值的加法逆元是他本身

比如10000000的加法逆元就是它本身

原因：
补码的最小值的绝对值其实是要比补码的最大值多1的

所以，单纯取负是找不到最小值的加法逆元，我们只能通过溢出的思想。

10000000+10000000 = 0

4. 乘法运算

• 无符号数乘法

对于向量\(x=[x_{w-1},x_{w-2},...,x_0]\)
对于向量\(y=[y_{w-1},y_{w-2},...,y_0]\)

对于\(z = x*y = [z_{2w-1},z_{2w-2},...,z_0]\)截取低w位就是最后的答案，也就是对\(2^w\)取模

11 = 1011
13 = 1101

11 * 13 = 10001111 = 11*13%16 = 15

• 有符号数乘法（补码乘法）

对于向量\(x=[x_{w-1},x_{w-2},...,x_0]\)
对于向量\(y=[y_{w-1},y_{w-2},...,y_0]\)

运算结果的位级表示与无符号数是相同的
按照无符号数运算得到的结果要将无符号数转换成有符号数

对于\(z = x*y = [z_{2w-1},z_{2w-2},...,z_0]\)截取低w位在转换为有符号数就是结果

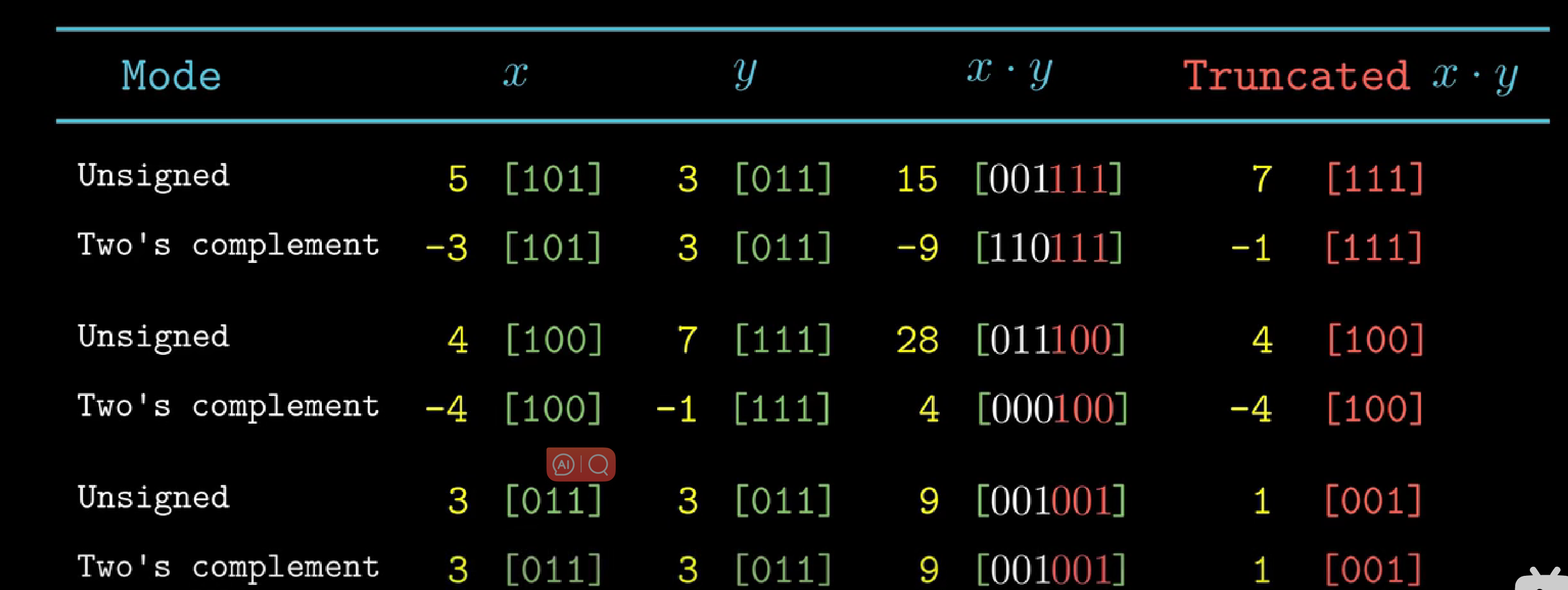
注：对于-3 * 3其实是111101*000011=110111 = -9

• 乘以常数

在大多数机器上，整数乘法指令相当慢，需要十个或更多时钟周期。
而其他整数运算（加，减，位级运算，移位）只需要一个时钟周期
因此编译器使用了一项优化：试着用移位和加法运算的组合来代替乘以常数因子的乘法

因为乘以2的k次幂 = 左移k位，又因为任何常数都能转化为二进制表示。那么我们来看下面这个例子

对于整数x*14这个运算可以表示为

\[\begin{align*} x*14&=x*(2^3+2^2+2^1)\\ &=(x<<3)+(x<<2)+(x<<1) \end{align*} \]

这样子一个乘法操作可以用三个移位操作和两个加法操作来代替

更好的编译器可能做出这种优化

\[\begin{align*} x*14&=x*(2^4-2^1)\\ &=(x<<4)-(x<<1) \end{align*} \]

这样子一个乘法操作可以用两个移位操作和一个减法操作来代替

5. 除以常数

在大多数机器上，整数除法比整数乘法还要慢（需要30个或更多的时钟周期）
我们同样可以用移位的方式来实现，只不过这次用的是右移

整数除法总是向0舍入 ：【3.14】=3 ， 【-3.14】=-3

• 无符号数除以常数
  其实就是无符号数逻辑右移k位，这没什么好说的

• 有符号数除以常数

  • 对于x>=0，效果与逻辑右移是一样的

  • 对于x<0，我们就要采取的是算数右移，这里面的细节我们重点说一下

下图中第一列k是右移位数，第二列是原数右移后的二进制表示

第三列是第二列的十进制表示，第四列是按照数学计算理论上应该得到的值(\(x/2^k\)计算后不舍入)

我们可以看到第三行的结果-771.25如果按照我们向0舍入的原则那么他应该是-771而不是-772，那么为什么会出现这个情况呢

我们可以先看一个简单的例子
让-3 和-4同时除以2（右移一位）

-3:1101
-4:1100
右移一位后：
-3:1110 = -2
-4:1110 = -2

我们发现对于-3/2预期结果是-1.5向0舍入是-1，但和上图一样得到了不符合我们除法原则的结果

其根本原因是右移时将末尾1舍弃了导致该位没有1和该位有1得到了一样的结果。

那么我们可不可以将要舍弃的1全部都向前进位，让他们的值不会被平白消失，这样就引出了偏置的概念

偏置：每次移k位前都先在原数上 + \(1<<k-1\),其实就是在低k位上每一位都加1来修正原本不合适的舍入

比如对于-12340（1100111111001100）右移4位之前我们先在末尾+1111

这样原位是0的话没有任何影响，最后都会被移掉。

但原位为1的话就会向前进1，将值保存下来

四. 浮点数

1. 定点表示法(非重点)

考虑含有小数值的二进制数字
\(b = b_mb_{m-1}...b_1b_0 . b_{-1}b_{-2}...b_{-n}\)

\(b =\sum_{i=-n}^{m} 2^i*b_i\)

例如

\[101.11 = 1*2^2+0*2^1+1*2^0+1*2^{-1}+1*2^{-2} = 5 \frac{3}{4} \]

2.IEEE浮点表示

定点表示法不能很有效的表示非常大的数字。

对于表达式\(5*2^{100}\) ，用定点表示法是用101后面跟着100个0的位模式来表示。
但我们更希望通过给定x和y的值，来表达形如\(x*2^y\)的数

IEEE格式：\(V = (-1)^s*M*2^E\)
\(s\):符号位，\(M\):尾数（<1）, \(E\):阶码

单精度浮点数float和双精度浮点数double的二进制位表示：

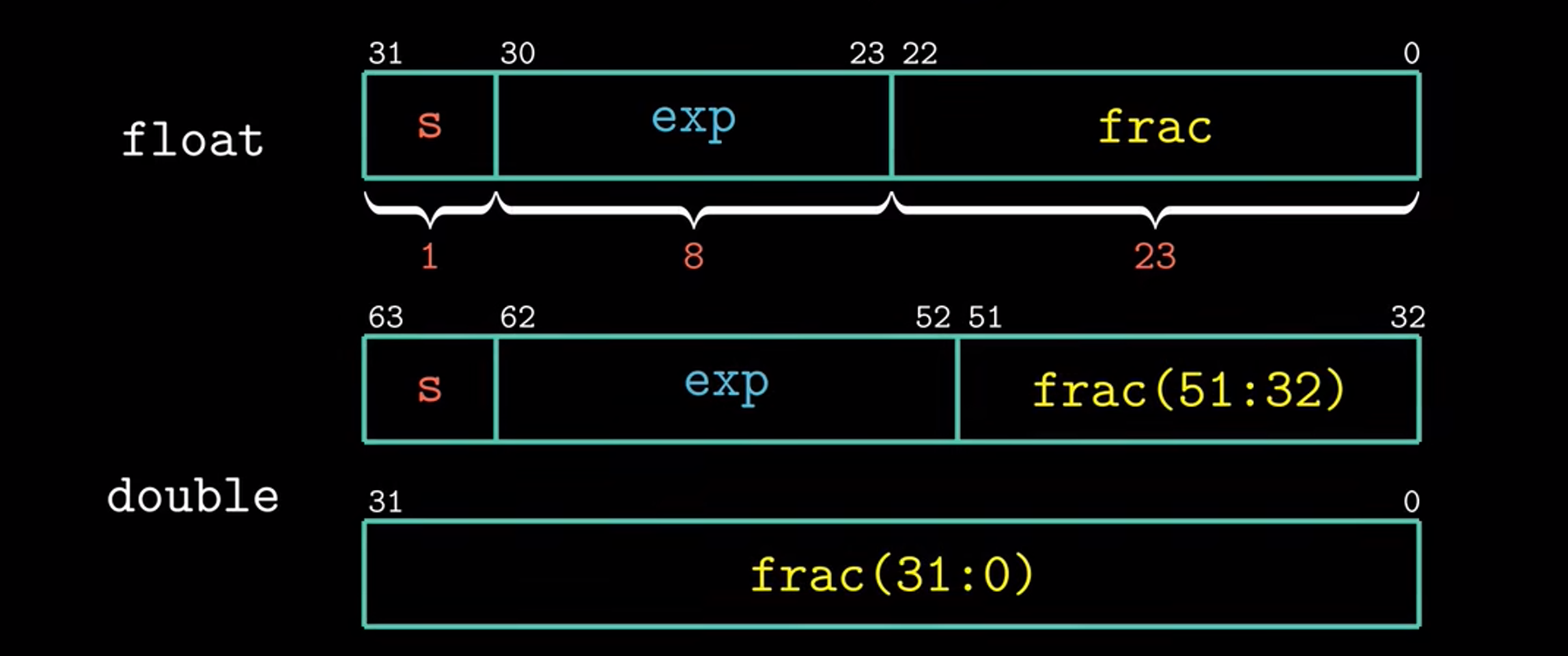
注 ： exp在浮点数中的表示其实是用移码表示
移码：移码 = 真值+偏移量Bias(\(2^{(n-1)}-1\))，对于上图就是\(2^{(8-1)}-1\)

根据exp的值，被编码的值可以分为三类:

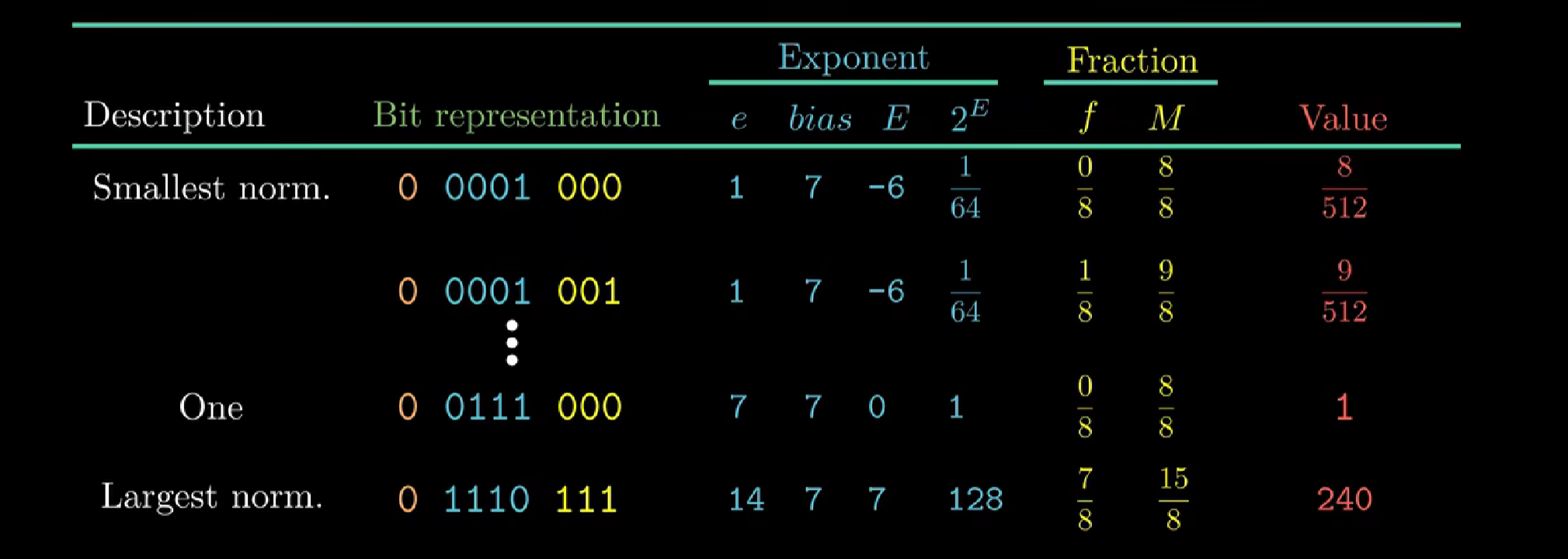
1. 规格化

阶码不是全0也不是全1

阶码的值是E = e-Bias，e是无符号数。由此产生指数的取值范围：-126~+127
尾数M = 1+f （\(M = 1.f_{n-1}f_{n-2}...f_0\)）

规格化数实例：
（红色为s,蓝色为exp，黄色为frac）

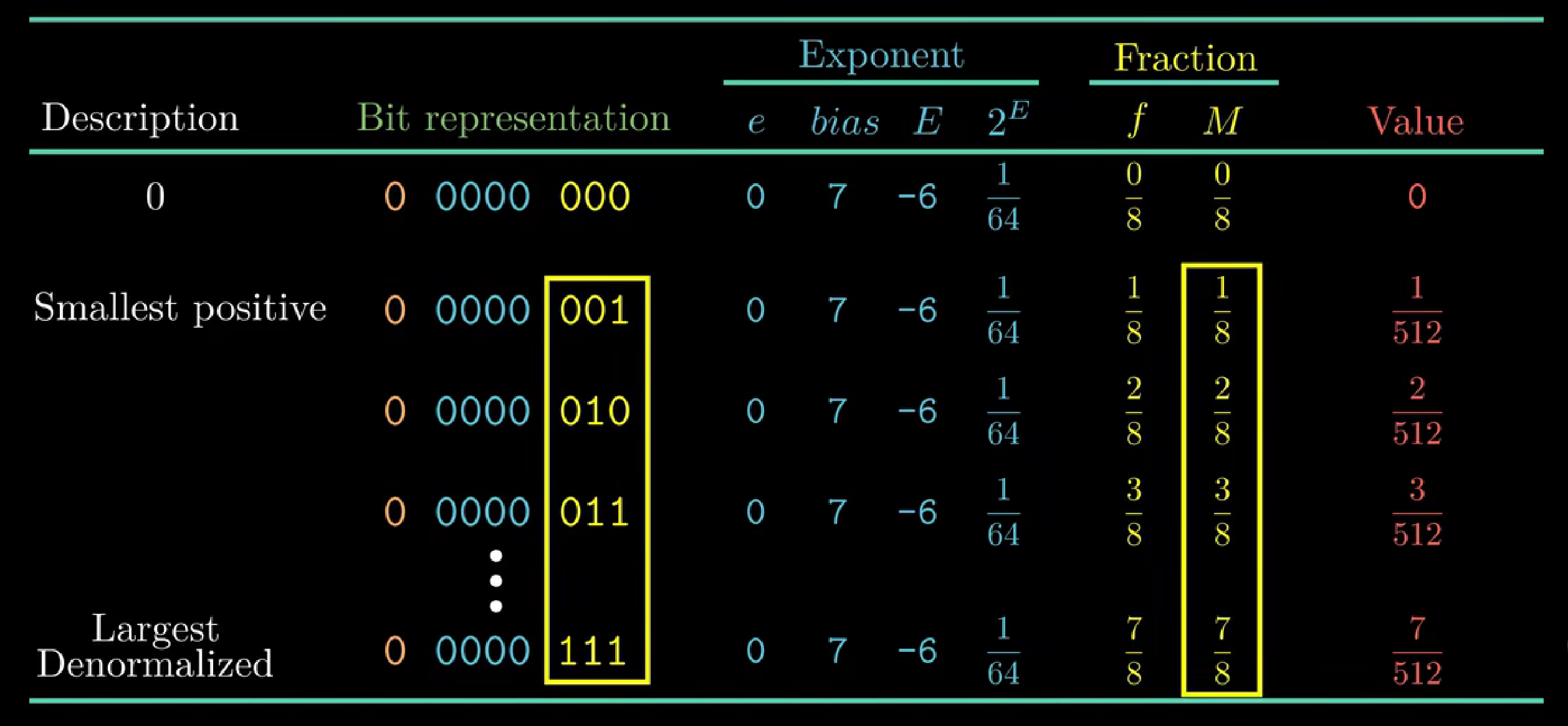
2. 非规格化

阶码全是0

非规格化的阶码值是E=1-Bias,尾数的值是M=f,不包含隐含的开头的1

非规格化将阶码值设为1-Bias而不是因为移码的原因设为-Bias似乎是反直觉的。我们将很快看到，这种方式提供了一种从非规格化值平滑转移到规格化值的方法

非规格化数有两个用途:

• 提供一种表示数值0的方法

在使用规格化数时，我们尾数总是有一个隐含的1，这样我们就不能表示0
当s=0,e = 0,f = 0,我们得到+0.0
s = 1,e = 0,f = 0,我们得到-0.0

• 表示那些非常接近于0.0的数

和表示0的理由一样，因为规格化的尾数恒大于1，所以0.xxx这种数需要用非规格化数表示

非规格化数实例：

3. 特殊值

• 无穷大
  

当我们把两个非常大的数相乘，或者除以零时，无穷能够表示溢出结果

• NaN(不是一个数)
  

当一些运算结果不是实数或无穷时，就会返回NaN，比如当计算根号-1，无穷-无穷时。

4. 舍入
   有四种舍入方式 ： 向上舍入，向下舍入，向零舍入，向偶数舍入
   对于一个浮点数，他有可能向上舍入也有可能向下舍入。如果他在两个可能值的中间则进行向偶数舍入来避免统计偏差

比如要求保留两位小数

1.2350000舍入为1.24,1.2450000舍入为1.24

5. 浮点运算

我们来看两个表达式：

• （3.14+1e10）-1e10 = 0
• 3.14+(1e10-1e10) = 3.14

对于第一个表达式这个结果是不可思议的，这是因为在进行3.14+1e10时候，运算结果会是float类型
\(3.14 = 11.0010001111010111000010100011110_2 = 0.00000000000000000000000000000000110010001111010111000010100011110 _2*2^{33}\)
\(1e10 = 10000000000 = 1001010100000010111110010000000000_2 = 1.001010100000010111110010000000000_2*2^{33}\)

因为结果是float类型，单精度浮点数的尾数只有23位，会发生截断,过程如下

\[\begin{align*} 3.14+1e10 = &1.00101010000001011111001(截断) \\ &000000000110010001111010111000010100011110*2^{33} \end{align*} \]

我们可以发现3.14+1e10截断后的位模式和1e10独自截断后是一样的，所以\((3.14+1e10)-1e10 = 0\)