树状数组
1. 引入
树状数组可以用logn的时间进行单点修改和区间求和
在传统数组中进行单点修改时间o1,区间求和on
前缀和数组中进行单点修改时间on,区间求和o1
树状数组则是两者取了个平均
2. 定义
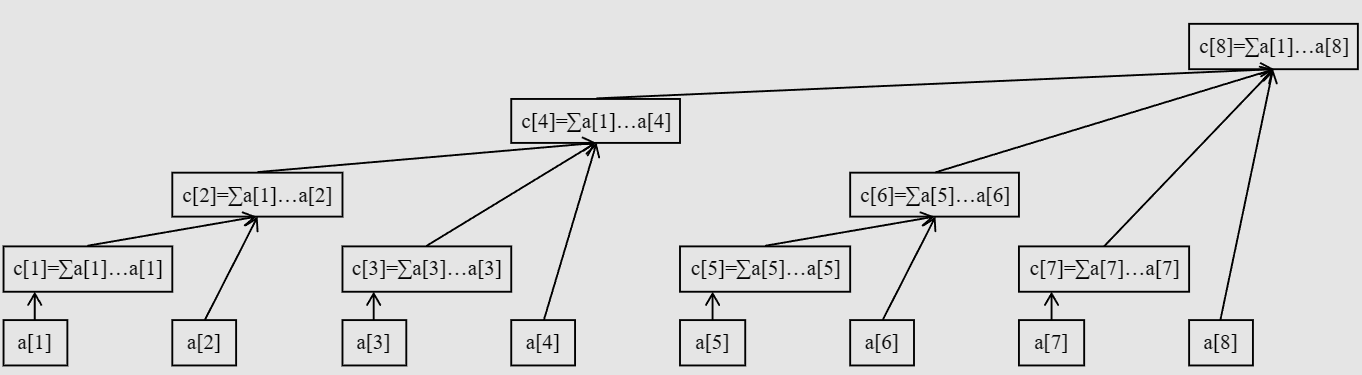
给定初始数组a1,a2,a3...an
设树状数组c1,c2,c3...cn
这么说可能有点抽象,我们可以这样理解
设\(a_i\)的二进制表示为???100 , 那么\(c_i\)就表示从\(a_{???001}\)一直加到\(a_{???100}\)
对于\(c_{100}\),它其实就是\(c_{010}+c_{011}+a_{100}\)
同理,\(c_{1000} = c_{0100}+c_{0110}+c_{0111}+a_{1000}\)
所以树状数组\(c_i\)其实就是维护一段区间的和,这个区间的长度为lowbit(i)
3. 操作
(1).查询区间1~x的和
int query(int x) //查询 1....x的区间和
{
int ans = 0;
for(;x;x-=x&(-x)) ans+=c[x];
return ans;
}
举个例子:
对于i = 10101,其实就是求 :
10101~10101 + 10001~10100 + 00001~10000
(2) . 修改a[i]的值(对a[i]+x)
void modify(int x,int s) //给第x个元素 + s
{
for(;x<=n;x+=x&(-x)) c[x] += s;
}
举个例子:
对于i = 101101 这个点+x
其实就是把c数组下标为101110,110000,1000000....的点+x,直到下标超过n
4. 例题
1. 树状数组模板题1 https://www.luogu.com.cn/problem/P3374
将某一个数加上 \(x\)
求出某区间每一个数的和
输入格式
第一行包含两个正整数 \(n(n<=5e5),m\),分别表示该数列数字的个数和操作的总个数。
第二行包含 \(n\) 个用空格分隔的整数,其中第 \(i\) 个数字表示数列第 \(i\) 项的初始值。
接下来 \(m\) 行每行包含 \(3\) 个整数,表示一个操作,具体如下:
1 x k含义:将第 \(x\) 个数加上 \(k\)
2 x y含义:输出区间 \([x,y]\) 内每个数的和输出格式
输出包含若干行整数,即为所有操作 \(2\) 的结果。
样例输入1
5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4
样例输出
14
16
没什么好说的,用这道题来引入一下板子
# include<bits/stdc++.h>
using namespace std;
const int N = 5e5+10;
int n,m;
int a[N],c[N];
int query(int x) //查询 1....x的区间和
{
int ans = 0;
for(;x;x-=x&(-x)) ans+=c[x];
return ans;
}
void modify(int x,int s) //给第x个元素 + s
{
for(;x<=n;x+=x&(-x)) c[x] += s;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++) {scanf("%d",&a[i]);modify(i,a[i]);}
while(m--)
{
int t;cin>>t;
if(t == 1)
{
int x,k;cin>>x>>k;
modify(x,k);
}
else
{
int x,y;cin>>x>>y;
cout<<query(y)-query(x-1)<<endl;
}
}
return 0;
}
2. 树状数组模板题2 https://www.luogu.com.cn/problem/P3368
已知一个数列,你需要进行下面两种操作:
-
将某区间每一个数加上 \(x\);
-
求出某一个数的值。
输入格式
第一行包含两个整数 \(N\)(\(N\)<=5e5)、\(M\),分别表示该数列数字的个数和操作的总个数。
第二行包含 \(N\) 个用空格分隔的整数,其中第 \(i\) 个数字表示数列第 $i $ 项的初始值。
接下来 \(M\) 行每行包含 \(2\) 或 \(4\)个整数,表示一个操作,具体如下:
操作 \(1\): 格式:1 x y k 含义:将区间 \([x,y]\) 内每个数加上 \(k\);
操作 \(2\): 格式:2 x 含义:输出第 \(x\) 个数的值。
输出格式
输出包含若干行整数,即为所有操作 \(2\) 的结果。
样例输入1
5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4
样例输出1
6
10
我们可以发现这道题想实现给区间每一个数加上x这个操作
我们如果还用原序列建树状数组然后在树状数组上进行操作,那么这个操作的复杂度将变成nlogn,这个复杂度我们显然是接受不了的
所以我们可以对原数组的差分数组建树状数组,这样操作1和操作2都能重新变成logn
# include<bits/stdc++.h>
using namespace std;
const int N = 5e5+10;
int n,m;
int a[N],c[N];
int query(int x) //查询 1....x的区间和
{
int ans = 0;
for(;x;x-=x&(-x)) ans+=c[x];
return ans;
}
void modify(int x,int s) //给第x个元素 + s
{
for(;x<=n;x+=x&(-x)) c[x] += s;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++) {scanf("%d",&a[i]);modify(i,a[i]-a[i-1]);}
while(m--)
{
int t;cin>>t;
if(t == 1)
{
int x,y,k;cin>>x>>y>>k;
modify(x,k);modify(y+1,-k);
}
else
{
int x;cin>>x;
cout<<query(x)<<endl;
}
}
return 0;
}
3. 用树状数组求逆序对 https://ac.nowcoder.com/acm/problem/15163
在一个排列中,如果一对数的前后位置与大小顺序相反,即前面的数大于后面的数,那么它们就称为一个逆序。一个排列中逆序的总数就称为这个排列的逆序数。比如一个序列为4 5 1 3 2, 那么这个序列的逆序数为7,逆序对分别为(4, 1), (4, 3), (4, 2), (5, 1), (5, 3), (5, 2),(3, 2)。
输入描述
第一行有一个整数n(1 <= n <= 100000), 然后第二行跟着n个整数,对于第i个数a[i],(0 <= a[i] <= 100000)。
输出描述
输出这个序列中的逆序数`
输入
5
4 5 1 3 2
输出
7
我们可以这样想 : 把数组a中的元素从前往后加入到树状数组c中,每加入一个元素a[i],都进行modify(a[i],1)这步操作。
比如此时遍历到a[i],那么我们先算一下1~a[i]-1在树状数组上的前缀和,得到的结果就是数组a前面有几个比a[i]小的元素
但是我们想得到的是逆序对,所以在操作前将数组a反转一下就行
# include<bits/stdc++.h>
# define int long long
using namespace std;
const int N = 5e5+10;
int n;
int a[N],c[N];
int query(int x) //查询 1....x的区间和
{
int ans = 0;
for(;x>0;x-=x&(-x)) ans+=c[x];
return ans;
}
void modify(int x,int s) //给第x个元素 + s
{
for(;x<=n;x+=x&(-x)) c[x] += s;
}
signed main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
reverse(a+1,a+n+1);
int ans = 0;
for(int i=1;i<=n;i++)
{
ans+=query(a[i]);
modify(a[i],1);
}
cout<<ans<<endl;
return 0;
}
4. 当空间被卡时用离散化+树状数组求逆序对
https://www.luogu.com.cn/problem/P1774
题目大意就是最少交换相邻的元素几次才能使整个序列变成一个不下降子序列
其实就是要求逆序对的数,因为每次将新的元素放入到树状数组中,就可以顺便使这个子序列变成不下降的,而这个操作的次数是这个子序列的逆序对数
数给的范围很大,我们必须对其进行离散化不然开不下2e9的树状数组
离散化其实就是根据数据的相对大小,将这些数重新赋值,保证相对大小不变
# include<bits/stdc++.h>
# define int long long
using namespace std;
typedef pair<int,int> pii;
int n;
const int N = 5e5+10;
int a[N],c[N];
pii b[N];
void add(int x,int s)
{
for(;x<=n;x+=x&(-x)) c[x]+=s;
}
int query(int x)
{
int ans = 0;
for(;x;x-=x&(-x)) ans+=c[x];
return ans;
}
bool cmp(pii a,pii b)
{
if(a.first == b.first) return a.second>b.second;
else return a.first>b.first;
}
signed main()
{
cin>>n;
int ans = 0;
for(int i=1;i<=n;i++) {cin>>a[i];b[i] = {a[i],i};}
sort(b+1,b+n+1,cmp);
for(int i=1;i<=n;i++) a[b[i].second] = i;
for(int i=1;i<=n;i++)
{
ans+=query(a[i]);
add(a[i],1);
}
cout<<ans<<endl;
return 0;
}
5. 树状数组上的二分(暂时只会logn^2的,单log的之后再补)
https://ac.nowcoder.com/acm/contest/61132/L
给定两个正整数n,m,再给定长度为n的正整数序列a, 保证n为奇数。接下来m行,每行两个正整数p, x。表示把a[p]修改为x。对于每次操作输出修改后的中位数。
输入
7 3 1 2 3 4 5 6 7 2 3 4 4 7 1输出
4 4 3
# include<bits/stdc++.h>
# define int long long
using namespace std;
typedef pair<int,int> pii;
int n;
const int N = 5e5+10;
int a[N],c[N];
pii b[N];
void add(int x,int s)
{
for(;x<=n;x+=x&(-x)) c[x]+=s;
}
int query(int x)
{
int ans = 0;
for(;x;x-=x&(-x)) ans+=c[x];
return ans;
}
bool cmp(pii a,pii b)
{
if(a.first == b.first) return a.second>b.second;
else return a.first>b.first;
}
signed main()
{
cin>>n;
int ans = 0;
for(int i=1;i<=n;i++) {cin>>a[i];b[i] = {a[i],i};}
sort(b+1,b+n+1,cmp);
for(int i=1;i<=n;i++) a[b[i].second] = i;
for(int i=1;i<=n;i++)
{
ans+=query(a[i]);
add(a[i],1);
}
cout<<ans<<endl;
return 0;
}
6. 二维树状数组 (其实和一维没啥区别)
# include<bits/stdc++.h>
# define ing long long
using namespace std;
const int N = 9e3+10;
int a[N][N],c[N][N];
int n,m;
void add(int x,int y,int k)
{
for(int a = x;a<=n;a+=a&(-a))
for(int b = y;b<=m;b+=b&(-b))
c[a][b]+=k;
}
int query(int x,int y)
{
int res = 0;
for(int a = x;a;a-=a&(-a))
for(int b = y;b;b-=b&(-b))
res+=c[a][b];
return res;
}
signed main()
{
cin>>n>>m;
int t;
while(cin>>t)
{
if(t == 1)
{
int x,y,k;cin>>x>>y>>k;
add(x,y,k);
}
else
{
int a,b,c,d;cin>>a>>b>>c>>d;
cout<<query(c,d)-query(a-1,d)-query(c,b-1)+query(a-1,b-1)<<endl;
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号