人工智能需要用到的数学

注： 这篇文章主要是以b站视频《学习人工智能必备的数学课》为主体，参考了几十篇博客并夹杂着个人很少的一点感悟的笔记。所以有很多地方可能大家在某些博客上看到过，轻喷qwq

1.人工智能中需要用到的数学知识总览

       1. 微积分(主要用到微分，作用是求函数的极值)

  • 导数和偏导数的定义与计算方法
  • 梯度向量的定义
  • 极值定理，可导函数在极值点处导数或梯度必须为0
  • 雅可比矩阵，这是向量到向量映射函数的偏导数构成的矩阵，在求导推导中会用到
  • Hession矩阵，这是二阶导数对多元函数的推广，与函数的极值有密切的联系
  • 凸函数的定义与判断方法
  • 泰勒展开公式
  • 拉格朗日乘数法，用于求解带等式约束的极值问题

最核心的是多元函数的泰勒展开公式，根据它我们可以推导处机器学习中常用的梯度下降法，牛顿法，拟牛顿法等一系列最优化方法


      2. 线性代数

  • 向量和它的各种运算，包括加法，减法，数乘，转置(transpose)，内积（dot）
  • 向量和矩阵的范数，L1范数和L2范数
  • 矩阵和它的各种运算，包括加法，减法，乘法，数乘
  • 逆矩阵的定义与性质
  • 行列式的定义与计算方法
  • 二次型的定义
  • 矩阵的正定性
  • 矩阵的的特征值与特征向量
  • 矩阵的奇异值分解
  • 线性方程组的数值解法，尤其是共轭梯度法

机器学习算法处理的数据一般都是向量、矩阵或者张量。经典的机器学习算法输入的数据都是特征向量，深度学习算法在处理图像时输入的2维的矩阵或者3维的张量。掌握这些知识会使你游刃有余


      3. 概率论

  • 随机事件与概率
  • 条件概率与贝叶斯公式
  • 随机变量
  • 随机变量的期望与方差
  • 常用概率分布（正太分布、均匀分布、伯努利二项分布）
  • 随机向量（联合概率密度函数）
  • 协方差与协方差矩阵
  • 最大似然估计

如果把机器学习所处理的样本数据看做随机变量/向量，我们就可以用概率论的观点对问题进行建模，这代表了机器学习中很大的一类方法


      4. 最优化

  • 凸优化
  • 拉格朗日对偶
  • KKT条件

几乎所有机器学习算法归根到底都是在求解最优化问题
求解最优化问题的思想是在极值点处函数的导数/梯度必须为0。因此你必须理解梯度下降法，牛顿法这两种常用的算法，它们的的迭代公式都可以从泰勒展开公式中得到。如果能知道坐标下降法、拟牛顿法就更好了


2. 线性代数

  1. 向量与其运算
    向量是线性代数里面最基本的概念，它其实就是一维数组，由N个数构成的，\(X = (X_1 , X_2 ...... X_n)\)

    \(X_1\)这些是向量的分量，向量的分量我们称之为维度，就像三维空间的向量有三个分量：x,y,z一样 , n维向量集合的全体就构成了n维欧式空间，\(R^n\)

  2. 行向量与列向量
    行向量是按行把向量排开，列向量是按列把向量排开
    行向量只有一行，列向量只有一列


    机器学习中数据x的每一行样本可以看成一个行向量，每一行都有n个特征（维度）组成 ， 也就是说一个特征在一列
    每个列向量都是所有样本的这一个特征的集合

  3. 向量的转置
    向量的转置其实就是将行向量变成列向量，将列向量变成行向量



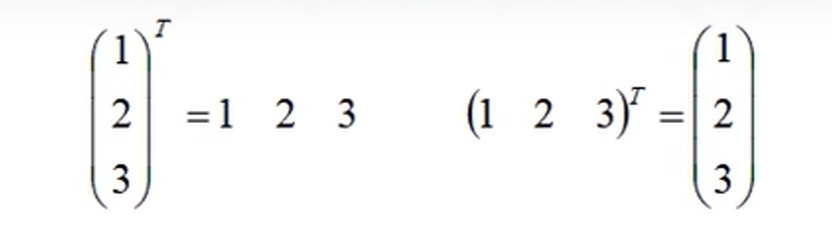
    一个列向量W的转置和一个列向量X的相乘 ： \(W_TX = w_1*x_1+w_2*x_2...w_n*x_n\)

  4. 向量的范数
    向量的范数就是把向量变成一个标量

\[p范数 ： ||x||_p = (\sum_{i=1}^n|x_i|^p)^ \frac{1}{p} \]

       1范数就是p = 1，记作L1。值为分量的绝对值的和，就是曼哈顿距离
       2范数就是p = 2,L2 = 向量的模，就是欧几里得距离

  1. 矩阵与其运算(m行n列)

  • 方阵 ： m = n

  • 对称矩阵 ： \(a_{ij}=a_{ji}\),肯定是个方阵 （将方阵转置就得到了它的对称矩阵）

  • 单位矩阵 ： 主对角线都是1，其他位置是0，一定是一个方阵，等同于数字里面的1

  • 对角阵 ： 主对角线非0，其他位置是0


    下图是对角阵

  • 矩阵的加减

  • 矩阵的转置 ： 将A的所有元素绕着一条从第1行第1列元素出发的右下方45度的射线作镜面反转，即得到A的转置。 \(a_{ij}变成a_{ji}\)

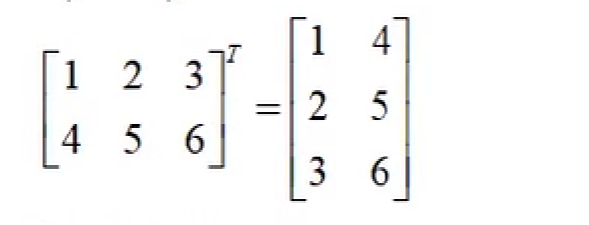
  • 矩阵乘法(满足分配率和结合律不满足交换律)
    把第一个矩阵的每一行，和第二个矩阵的每一列拿过来做内积得到结果
    如下图
    第1行与第1列的内积得到\(A_{11}\)
    第1行与第2列的内积得到\(A_{12}\)
    第2行与第1列的内积得到\(A_{21}\)
    第2行与第2列的内积得到\(A_{22}\)

    \(m*n\)的矩阵和\(n*k\)的矩阵相乘得到\(m*k\)的矩阵

    还有一个特殊的转置公式

\[(AB)^T = B^TA^T \]

  • 逆矩阵
    假设有一个矩阵A，注意它一定是方阵，乘以矩阵B等于单位矩阵I
    \(AB=I 或者 BA=I\) 那么我们称B为A的右逆矩阵和左逆矩阵。
    如果这样的B存在的话，它的左逆和右逆一定相等，统称为A的-1
    对线性方程组\(AZ=B\)同时乘A的逆，那么\(Z=B*A^{-1}\)

\[(AB)^{-1} = B^{-1}A^{-1} \]

\[(A^{-1})^{-1} = A \]

\[(A^T)^{-1} = (A^{-1})^T \]

  1. 矩阵的行列式
    一个矩阵必须是方阵才能计算它的行列式。行列式是把矩阵变成一个标量

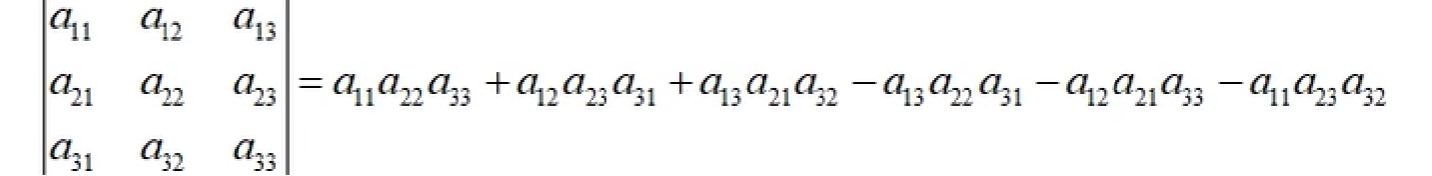
  1. 特征值和特征向量
  • 定义
    设A为n阶方阵，若存在一个数\(\lambda\)和非零向量\(\alpha\)使得\(A\alpha=\lambda\alpha\),\(\lambda\)为矩阵\(A\)的特征值，\(\alpha\)为特征值\(\lambda\)的特征向量

\[\begin{bmatrix} 1&0\\1&2 \end{bmatrix} \begin{bmatrix} 0\\1 \end{bmatrix}= \begin{bmatrix} 0\\2 \end{bmatrix}= 2 \begin{bmatrix} 0\\1 \end{bmatrix} \]

所以\(\lambda\) = 2是特征值,\(\begin{bmatrix} 0\\1 \end{bmatrix}\)是\(\lambda\)的特征向量
\(A\alpha=\lambda\alpha\)也可写成\((|A-\lambda I|=0)\) \(I\)是单位矩阵
拿上面式子举例

\[|\lambda I-A|= \begin{bmatrix} \lambda-1&&0\\-1&&\lambda-2 \end{bmatrix}=0 \]

\[\lambda ^2-3\lambda+2=0 \]

\[(\lambda-1)(\lambda-2)=0 \]

有一个特征值为1，一个特征值为2

  • 性质
    A矩阵主对角线的值加和等于所有特征值\(\lambda\)的和
    所有特征值的乘积等于A的行列式的值


8. 二次型 二次型就是纯二次项构成的一个函数，通过矩阵来研究二次函数（方程） 如果一个多元二次函数的每一项的变量次数都是2，则称这个二次函数是齐次的，即二次型 $f(x_1,x_2)=ax_1^2+bx_1x_2+cx_2^2$就是二次型
$$ x^2-xy+y^2=1 可以写作 $$ $$ \begin{bmatrix} x&y \end{bmatrix} \begin{bmatrix} 1&-0.5\\-0.5&1\\ \end{bmatrix} \begin{bmatrix} x\\y \end{bmatrix} =1 $$

\(\begin{bmatrix} 1&-0.5\\-0.5&1\\ \end{bmatrix}\)就是二次型矩阵,记作\(x^Twx+b\)

3. 微积分

  1. 导数与凹凸性的关系
    如果\(f''(x) > 0\) 则函数是凸函数
    驻点为函数增减性的交替点，拐点是凹凸性的交替点
    \(x^3\) 当x<0是凹函数，x>0是凸函数
  2. 一元函数泰勒展开

\[f(x)=f(x_0)+\frac{f'(x_0)(x-x_0)}{1!}+\frac{f''(x_0)(x-x_0)^2}{2!} + \frac{f^n(x_0)(x-x_0)^n}{n!} + R_n(x) \]

      泰勒展开是通过多项式函数来近似一个可导函数f(x)，在x = x0处进行泰勒展开

      泰勒展开在机器学习里用来求函数的极值，很多时候f(x)可能会非常复杂，我们
      去用泰勒展开做一个近似，梯度下降法就是只保留泰勒展开一阶项，牛顿法是
      二阶项。
3. 偏导数
对于多元函数，我们把其他的自变量固定不动，看成是常量，我们对其他的某一个变量求导数的话，那就是偏导数
\(f(x,y) = x^2+xy-y^2\) 对x求偏导\(\frac{\partial f}{\partial x} = 2x+y\) 对y求导$\frac{\partial f}{\partial y} = x-2y $
考虑高阶偏导数
\(\frac{\partial f}{\partial x \partial y}\) 是f对x求偏导再对y求偏导

\(f(x,y)=x^2+xy-y^2\)
对x求偏导 = 2x+y 再对y求偏导 = 1
4. 方向导数和梯度（gradient）

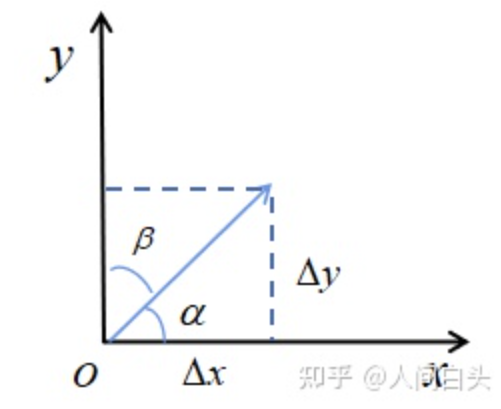
  • 方向导数是，给定方向的变化率（标量）
    如上图，方向\((cos\alpha,cos\beta)\)的导数就是将函数对x的偏导和对y的偏导都投影到这个方向
    对x偏导在对应方向投影为\(f_x'(x,y)cos\alpha\) , 对y偏导在对应方向投影为\(f_y'(x,y)cos\beta\)

    所以方向导数为

\[f_{(cos\alpha,cos\beta)}'(x,y) = f_x'(x,y)cos\alpha+f_y'(x,y)cos\beta \]

  • 梯度 （一个向量）
    梯度是指函数值增长最快的方向。也就是方向导数最大值的方向就是梯度
    \(\bigtriangledown f(x) = (\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2}...\frac{\partial f}{\partial x_n})\)

  1. 多元函数泰勒展开

  2. 雅可比矩阵
    假设y是一个从n维欧氏空间映射到到m维欧氏空间的函数,每个\(y_i\)是单独从\(x_i\)映射过来的函数

    \(y = f(x)\) 中x有n个分量 ， \(x_i=(x_{i1},x_{i2},...x_{in})\)
    y有m个分量 \(y_i = f(x_i)\)
    雅可比矩阵就是每个\(y_i\)分别对每个\(x_i\)求偏导，构成的矩阵就是雅可比矩阵，如下图


7. Hessian矩阵
Hessian矩阵是一个n*n的矩阵，所有元素是二阶偏导数构成的，hessian是沿着主对角线对称的矩阵
具体如下

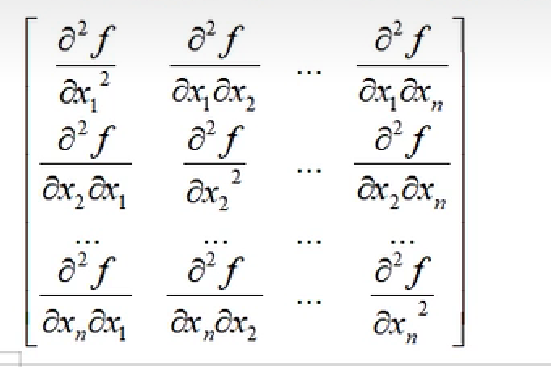
Hessian矩阵和函数的凹凸性关系密切，如果Hessian正定，f(x)是凸函数，负定是凹函数

4. 概率论

  1. 条件概率
    条件概率是针对两个或更多个有相关关系/因果关系的随机事件而言的
    对两个随机事件A和B而言，在A发生的情况下B发生的概率，那记住P(B|A),它等于AB同时发生的概率除以A发生的概率

\[p(b|a)= \frac {p(a,b)}{p(a)} \]

\[p(a|b)= \frac {p(a,b)}{p(b)} \]

  1. 贝叶斯公式
    P(B|A),它等于AB同时发生的概率除以A发生的概率

\[p(a|b)= \frac {p(a)*p(b|a)}{p(b)} \]

\[p(b)p(a|b)=p(a,b)=p(a)p(b|a) \]

  1. 随机事件的独立性
    两个事情是不想关的，b在a发生的条件下发生的概率是等于b本身发生的概率

\[p(b|a) = p(b) \]

\[p(a,b)=p(a)*p(b) \]

我们可以给他推广到n个事件相互独立的情况上面去，n个事件同时发生的概率等于n个事件的连乘

\[p(a_1...a_n)= \prod _{i=1}^{n}p(a_i) \]

  1. 随机变量
  • 离散型随机变量
    取值只可能是有限个可能，或者是无穷可列个。比如从0到$+\infty $,但是一定是能用整数编号编出来

  • 连续型随机变量
    它的取值是不可列个，比如0到1之间所有的实数

  • 一些公式
    对于离散型随机变量

\[p(x=x_i)=p_i \]

\[p_i>=0 \]

\[\sum p_i=1 \]

对于连续型随机变量，利用它的概率密度函数f(x)来定义

\[f(x)>=0 \]

\[\int_{-\infty}^{+\infty}f(x)dx=1 \]

\[落在区间范围（x1,x2）的概率=\int_{x_1}^{x_2}f(x)dx \]

  1. 数学期望
    数学期望就是概率意义下的平均值

    对于离散型，如果买彩票有0.2概率中500万,0.3概率中1万，0.5概率中0.1万
    那么数学期望=\(500*0.2+1*0.3+0.1*0.5\)

    对于连续型，求一个广义积分就是数学期望

\[E(x)=\sum x_ip(x_i) \]

\[E(x)=\int_{-\infty}^{+\infty}xf(x)dx \]

  1. 方差
    反应数据的波动程度

\[D(x)=\sum(x_i-E(x))^2p(x_i) \]

利用期望的线性性质：

\[E(a+bX)=a+bEX \]

\[E(X-\mu)^2=E(X^2-2\mu X+\mu ^2)=EX^2-2\mu EX+\mu ^2 \]

  1. 随机向量
    线代中，我们把标量x推广到向量，就是它有多个分量。

    一般地，对某一个随机试验涉及的n个随机变量\(X_1 , X_2...X_n\)称为n维随机向量或n维随机变量

    随机向量本质上还是一个从样本空间映射到实数空间的函数，只不过自变量从一个随机变量变成n个随机变量
  • 离散型随机向量
    \(P(x=x_i)\)
  • 续型随机变量
    下面是二维随机向量

\[f(x_1,x_2)>=0 \]

\[\int _ {-\infty}^{+\infty}f(x1,x2)dx_1dx_2=1 \]

  1. 协方差
    协方差是对于方差的推广，对于两个随机变量，它们的协方差反应它们两个之间的线性相关程度，把x2换成x1就是方差

\[cov(x_1,x_2)=E((x_1-E(x_1))(x_2-E(x_2))) \]

\[cov(x_1,x_2)=E(x_1x_2)-E(x_1)E(x_2) \]

对于n维的向量X，它的协方差就构成了一个协方差矩阵，第i行第j个是\(x_i\)和\(x_j\)的协方差

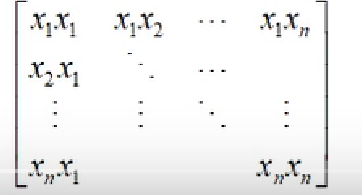
显然这是一个对称阵，这在机器学习里面会经常用到

  1. 最大似然估计
    极大似然估计就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值！
    对于这个函数：\(p(x|\theta)\)

    输入有两个：x表示某一个具体的数据；θ表示模型的参数。

    如果θ 是已知确定的，x是变量，这个函数叫做概率函数(probability function)，它描述对于不同的样本点x，其出现概率是多少。

    如果x是已知确定的，θ是变量，这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数，出现x这个样本点的概率是多少。
  • 似然函数
    概率\(p(x|\theta)\) 是在已知参数\(\theta\)的情况下，发生观测结果\(x\)的可能性大小；
    似然性\(L(\theta | x)\)是从观察结果x出发，分布函数参数为\(\theta\)的可能性大小

\[L(\theta|x)=p(x|\theta) \]

  • 最大似然估计
    对于给定的预测数据x,我们希望从所有参数\(\theta _1,\theta _2,...,\theta _n\)中找出最大概率生成数据观测数据的参数\(\theta ^*\)作为估计结果

\[L(\theta^*|x)=p(x|\theta^*)>=p(x|\theta)=L(\theta|x),\theta=\theta_1,...,\theta_n \]

而这最大化的步骤就是通过求导=0来解得

\[L(\theta|x)= p(x|\theta)=\prod _{i=1}^np(x_i;\theta) \]

要找到最大概率生成x的参数，即找到当\(L(\theta|x)\)取最大值时的\(\theta\),通过求导=0求出最大值
因为是连乘，对其求导很麻烦，所以两边同时取对数，将其变成连加，然后求导=0求解

posted @ 2023-09-02 05:11  拾墨、  阅读(109)  评论(0)  编辑  收藏  举报