背包问题
引入
有 n 个物品和一个容量为 W 的背包，每个物品有重量 w{i}和价值 v{i}两种属性，要求选若干物品放入背包使背包中物品的总价值最大且背包中物品的总重量不超过背包的容量。
我们之后涉及到的所有背包问题都会根据这个背景展开
1. 01背包
每个物品只能选取一次。
这样每个物品都会只有两种状态 ： 选与不选。用二进制表示就是0与1
也就是01背包
例题
有 n 种物品要放到一个袋子里，袋子的总容量为 m，第 i 种物品的体积为 vi，把它放进袋子里会获得 wi 的收益，每种物品至多能用一次，问如何选择物品，使得在物品的总体积不超过 m 的情况下，获得最大的收益？请求出最大收益。
输入格式
第一行两个整数 n,m。接下来 n 行，每行两个整数 vi,wi。
输出格式
一个整数，表示答案。样例输入
5 10
5 3
3 6
7 8
5 9
2 4
样例输出
19
数据规模
对于所有数据，保证 1≤n,m,vi,wi≤1000。
二维数组的解决方式
我们先来思考最直接的方式
设置一个dp数组 f[i][j] 代表从前i个物品里选，背包容量为j的时候的最大收益
对于每一个物品，都有选与不选两种方式。那么对于状态f[i][j]只可能是由两种状态转移过来的 ： 选第i个物品的f[i-1][j-v[i]]+w[i]和不选第i个物品的f[i-1][j]
状态转移方程为:
f[i][j] = max(f[i-1][j] , f[i-1][j-v[i]]+w[i])
代码如下
# include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
pii a[1010];
int f[1010][1010];
int main()
{
int n,m;cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i].second>>a[i].first;
for(int i=1;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
if(a[i].second>j) f[i][j] = f[i-1][j];
else
{
f[i][j] = max(f[i-1][j],f[i-1][j-a[i].second]+a[i].first);
}
}
}
cout<<f[n][m];
return 0;
}
一维数组的解决方式
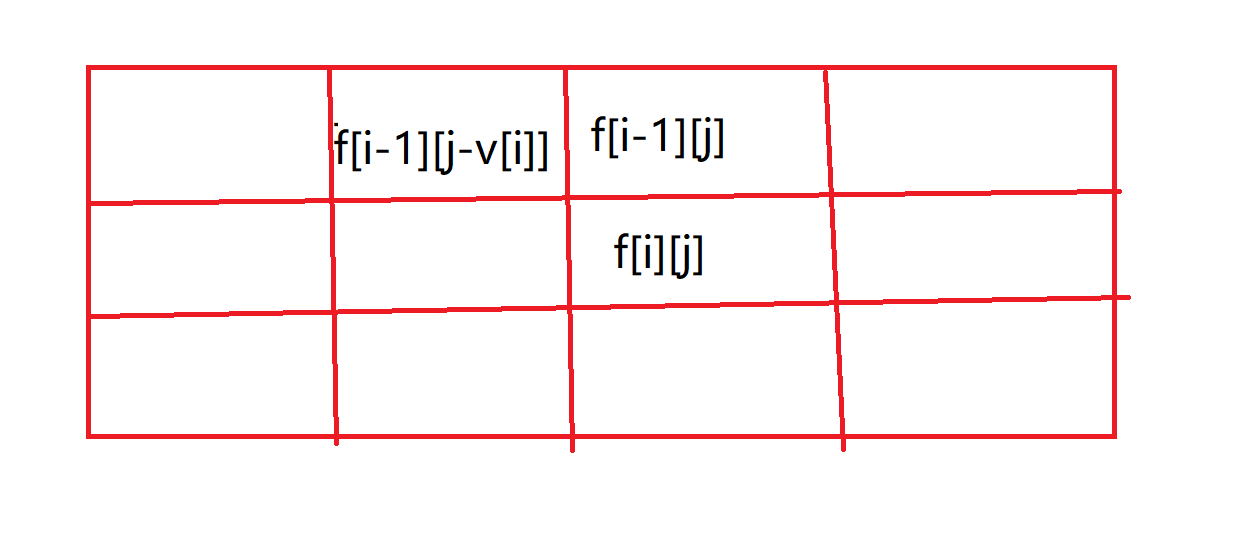（图丑莫怪qwq）
我们可以看到在二维数组中f[i][j]是由他上面的元素和左上方的两个元素转移过来的
那么我们发现求一个元素其实只需要知道他上一行的特定的两个元素就行。对f[i]有影响的只有f[i-1]这一维，那我们将f[i-1]这一维拷贝到f[i]上完全可以变成
f[i][j] = max(f[i][j] , f[i][j-v[i]]+w[i])
与其把f[i - 1]这一层拷贝到f[i]上，不如只用一个一维数组了，只用f[j]（一维数组，也可以理解是一个滚动数组 。转移方程就变成了
f[j] = max(f[j],f[j-v[i]]+w[i])
代码
# include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
pii a[1010];
int f[1011];
int main()
{
int n,m;cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i].first>>a[i].second;
for(int i=1;i<=n;i++)
{
for(int j = m;j>=a[i].first;j--) //因为遍历物品是从前往后遍历的，如果j从前往后遍历的话，f[j]都是由考虑前i个物品的状态转移过来的，但我们希望的由考虑前i-1个物品的状态转移过来的，所以j从后往前遍历
f[j] = max(f[j],f[j-a[i].first]+a[i].second);
}
cout<<f[m]<<endl;
return 0;
}
01背包的状态转移方程和优化到这里就讲完了，其他背包问题都是基于这个问题展开的，以后的证明部分就不会像01这样讲的那么详细了
2. 完全背包
完全背包与 0-1 背包的区别仅在于一个物品可以选取无限次，而非仅能选取一次。
那么转移方程就变成了 f[i][j] = max(f[i-1][j],f[i][j-v[i]]+w[i]
二维数组代码
# include<bits/stdc++.h>
using namespace std;
int v[1111],w[1111],f[1111][1111];
int main()
{
int n,m;cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
for(int i=1;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
if(j<v[i]) f[i][j] = f[i-1][j];
else f[i][j] = max(f[i-1][j],f[i][j-v[i]]+w[i]);
}
}
cout<<f[n][m]<<endl;
return 0;
}
一维数组代码
# include<bits/stdc++.h>
using namespace std;
int f[1111],v[1111],w[1111];
int main()
{
int n,m;cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
for(int i=1;i<=n;i++)
{
for(int j=v[i];j<=m;j++) f[j] = max(f[j],f[j-v[i]]+w[i]);
}
cout<<f[m];
return 0;
}
3. 多重背包
多重背包也是01背包的一个变式。与01背包的区别在于每种物品有k[i]个，而非一个。
一个很朴素的想法就是把每个物品有k个看成01背包，k个物品只有取与不取两种
直接放代码
# include<bits/stdc++.h>
using namespace std;
int v[111111],w[1111111],l[1111111],f[1111111];
int main()
{
int n,m;cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i]>>l[i];
for(int i=1;i<=n;i++)
{
for(int k=1;k<=l[i];k++)
{
for(int j=m;j>=v[i];j--)
{
f[j] = max(f[j],f[j-v[i]]+w[i]);
}
}
}
cout<<f[m];
return 0;
}
考虑优化 我们想要让取0,1...n[i]件这个效率很低的枚举被更好的枚举方式所替代
也就是有更好的一组数，其数量比n[i]小，在这组数里取若干件可以代换n[i]这组数里的任何一个值 。 这也就是二进制枚举
下图来自dd大牛的背包九讲
代码
# include<bits/stdc++.h>
using namespace std;
int v[2222],w[2222],l[2222],f[2222];
int main()
{
int n,m;cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i]>>l[i];
for(int i=1;i<=n;i++)
{
int res = l[i];
for(int k=1;k<=res;res-=k,k*=2)
{
for(int j=m;j>=v[i]*k;j--)
{
f[j] = max(f[j],f[j-v[i]*k]+w[i]*k);
}
}
for(int j=m;j>=v[i]*res;j--) f[j] = max(f[j],f[j-v[i]*res]+w[i]*res);
}
cout<<f[m]<<endl;
return 0;
}
4. 分组背包
有 n 件物品和一个大小为 m 的背包，第 i 个物品的价值为 w_i，体积为 v_i。同时，每个物品属于一个组，同组内最多只能选择一个物品。求背包能装载物品的最大总价值。
与01背包不同的是这个是每组只能选一个，那么对这个组进行01背包就好了
代码
# include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
vector<pii> a[1010];
int f[1111];
int main()
{
int n,m;cin>>n>>m;
int cnt = 1;
for(int i=0;i<n;i++)
{
int x,v,w;scanf("%d%d%d",&x,&v,&w);
cnt = max(cnt,x);
a[x].push_back({v,w});
}
for(int i=1;i<=cnt;i++)
{
for(int j = m;j>=0;j--)
{
for(auto k:a[i])
{
if(j>=k.first) f[j] = max(f[j],f[j-k.first]+k.second);
}
}
}
cout<<f[m]<<endl;
return 0;
}
关于这三层的遍历顺序的解释
第二层和第三层之所以不能调换的原因是一旦调换这个分组就会变成一个多重背包，变成了每组的物品全都可以取而不是只能取一个了
5. 二维费用背包
与01背包不同的是选一个物品会消耗两种价值（经费、时间），只需在状态中增加一维存放第二种价值即可。
例题
有 n 种物品要放到一个袋子里，袋子的总容量为 m，我们一共有 k 点体力值。第 i 种物品的体积为 vi，把它放进袋子里会获得 wi 的收益，并且消耗我们 ti 点体力值，每种物品只能取一次。问如何选择物品，使得在物品的总体积不超过 m 并且花费总体力不超过 k 的情况下，获得最大的收益？请求出最大收益。
输入格式
第一行三个整数 n,m,k。接下来 n 行，每行三个整数 vi,wi,ti。
输出格式
一个整数，表示答案。样例输入
5 10 10
3 8 3
4 10 2
5 1 5
1 10 4
4 4 1
样例输出
28
数据规模
对于所有数据，保证 1≤n,m,k,vi,wi,ti≤100。
代码
# include<bits/stdc++.h>
using namespace std;
int f[111][111];
struct object
{
int v,w,t;
}a[111];
int main()
{
int n,m,k;cin>>n>>m>>k;
for(int i=1;i<=n;i++) cin>>a[i].v>>a[i].w>>a[i].t;
for(int i=1;i<=n;i++)
{
for(int j=m;j>=a[i].v;j--)
{
for(int t=k;t>=a[i].t;t--) f[j][t] = max(f[j][t] , f[j-a[i].v][t-a[i].t]+a[i].w);
}
}
cout<<f[m][k];
return 0;
}
