拓扑排序
定义 : 对一个有向图构造拓扑序列，排序类似流程图那样按先干什么后干什么这样排序
拿大学教学安排举个例子（图来自oi wiki）
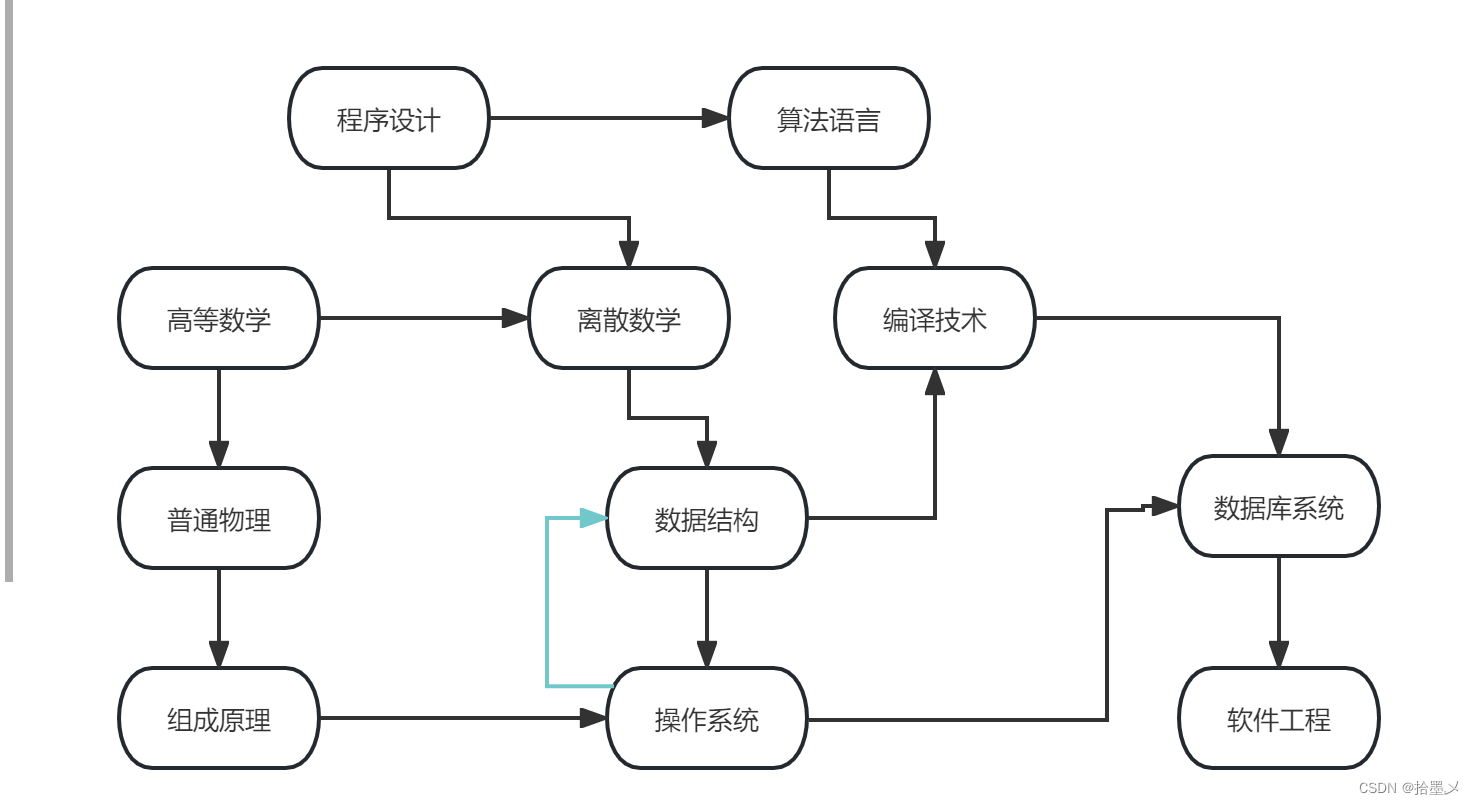
先不要考虑操作系统到数据结构那条蓝线 。
那么我们要先学程序设计才能学习后面的算法语言，离散数学等等。那么在拓扑序列中，程序设计就要在算法语言，离散数学这些前面。
但拓扑序列并不是唯一的，比如高等数学和程序设计是互不影响的，那么在拓扑序列中高等数学和程序设计谁在前谁在后都可以
现在让我们考虑操作系统到数据结构那条蓝线 。
现在操作系统和数据结构都互为各自的前置知识，这样就会出现矛盾，不知道拓扑序列中究竟该谁在前谁在后。
我们可以发现 : 一个图中所有点是否可以构成拓扑序列可以作为这个图是否存在有向环的判断标准
算法流程
1.初始化出所有点的入度，和每个点连接了哪个点，并用优先队列存每个点的入度
- 每次去优先队列的队头（有着最小入度的点），如果入度不为0且拓扑序列还没形成则证明图中存在有向环。否则将该点加入拓扑序列且将与之连有边的点入度--，并加到优先队列中
3.当拓扑序列生成（加入到序列的点的数量 == n） 退出循环即可
例题1 ： 拓扑排序板子（有向图判断）
给你一张 n 个顶点 m 条边的有向简单图，顶点编号从 1 到 n，你需要判断这张图中是否存在环。
如果存在环，则输出 Yes，否则输出 No。
输入格式
第一行两个整数 n,，表示图的顶点数和边数。接下来 m 行，每行两个整数 x,y，表示 x 号点到 y 号点有一条有向边。
输出格式
输出一行一个字符串表示答案。样例输入
4 4
1 2
2 3
3 4
1 4
样例输出
No
数据规模
对于所有数据，保证 2≤n≤10000,0≤m≤100000,1≤x,y≤n
代码
# include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
const int N = 1e4+10;
int n,m;
int dist[N]; //dist存的是这个点的入度是多少
vector<int> edge[N]; //edge[x]中存的是所有与x连有边的点
priority_queue<pii,vector<pii>,greater<pii> > q; //在优先队列中存dist[i],i
int main()
{
cin>>n>>m;
for(int i=0;i<m;i++)
{
int x,y;scanf("%d%d",&x,&y);
edge[x].push_back(y);dist[y]++;
}
for(int i=1;i<=n;i++) q.push({dist[i],i});
bool flag = false;
int tot = 0; //进入拓扑序列的点的数量
while(q.size())
{
auto t = q.top();q.pop();
if(t.first > 0) //如果最小入度点的入度>0,并且拓扑序列还没形成，那么证明存在有向环
{
flag = true;
break;
}
tot++;
if(tot == n) break;
for(auto i : edge[t.second])
{
dist[i]--; //把每个进入拓扑序列的点的所有与之形成边的点入度--，并加入队列中
q.push({dist[i],i});
}
}
if(flag) cout<<"Yes\n";
else cout<<"No\n";
return 0;
}
例题2 字典序最小拓扑序
给你一张 n 个顶点 m 条边的有向无环图，顶点编号从 1 到 n，请求出这张图的字典序最小的拓扑序列。
输入格式
第一行两个整数 n,m，表示图的顶点数和边数。接下来 m 行，每行两个整数 x,y，表示 x 号点到 y 号点有一条边。
输出格式
输出一行 n 个数表示字典序最小的拓扑序列。样例输入
4 3
1 2
2 3
4 2
样例输出
1 4 2 3
数据规模
对于所有数据，保证 2≤n≤10000,0≤m≤100000,1≤x,y≤n,x≠y
在我们的拓扑排序的板子中，我们存入度数就是用的小根堆
priority_queue
那么我们可以自然地想到用小根堆存一个pair类型，pair的第一个元素是入度数，第二个元素是点的序号
代码
# include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
const int N = 1e4+10;
int n,m;
vector<int> edge[N];
int dist[N];
vector<int> ans;
priority_queue<pii,vector<pii>,greater<pii> > q;
int st[N];
int main()
{
cin>>n>>m;
for(int i=0;i<m;i++)
{
int x,y;scanf("%d%d",&x,&y);
edge[x].push_back(y);
dist[y]++;
}
for(int i=1;i<=n;i++) q.push({dist[i],i});
int tot = 0;
while(q.size())
{
auto t = q.top();q.pop();
if(st[t.second]) continue;
tot++;
ans.push_back(t.second);
if(tot == n) break;
st[t.second] = true;
for(auto i:edge[t.second])
{
dist[i]--;
q.push({dist[i],i});
}
}
for(auto x:ans) cout<<x<<" ";
return 0;
}
