20182307 2019-2020-1 《数据结构与面向对象程序设计》实验九报告
20182307 2019-2020-1 《数据结构与面向对象程序设计》实验九报告
课程:《程序设计与数据结构》
班级: 1823
姓名: 陆彦杰
学号:20182307
实验教师:王志强
实验日期:2019年12月2日
必修/选修: 必修
目录
1.实验内容
- (1) 初始化:根据屏幕提示(例如:输入1为无向图,输入2为有向图)初始化无向图和有向图(可用邻接矩阵,也可用邻接表),图需要自己定义(顶点个数、边个数,建议先在草稿纸上画出图,然后再输入顶点和边数)(2分)
- (2) 图的遍历:完成有向图和无向图的遍历(深度和广度优先遍历)(4分)
- (3) 完成有向图的拓扑排序,并输出拓扑排序序列或者输出该图存在环(3分)
- (4) 完成无向图的最小生成树(Prim算法或Kruscal算法均可),并输出(3分)
- (5) 完成有向图的单源最短路径求解(迪杰斯特拉算法)(3分)
- PS:本题12分。目前没有明确指明图的顶点和连通边,如果雷同或抄袭,本次实验0分。
2. 实验过程及结果
初始化矩阵
- 实验目的:通过自定义结点、边的个数与对应的权值,构造出有向图和无向图的邻接矩阵
- 实验思路:
- 将之前课程实践中的提前固定邻接矩阵代码,改为自己输入。关键步骤在于将连接边、设置点的语句中的常量改为变量,通过键盘输入得到。

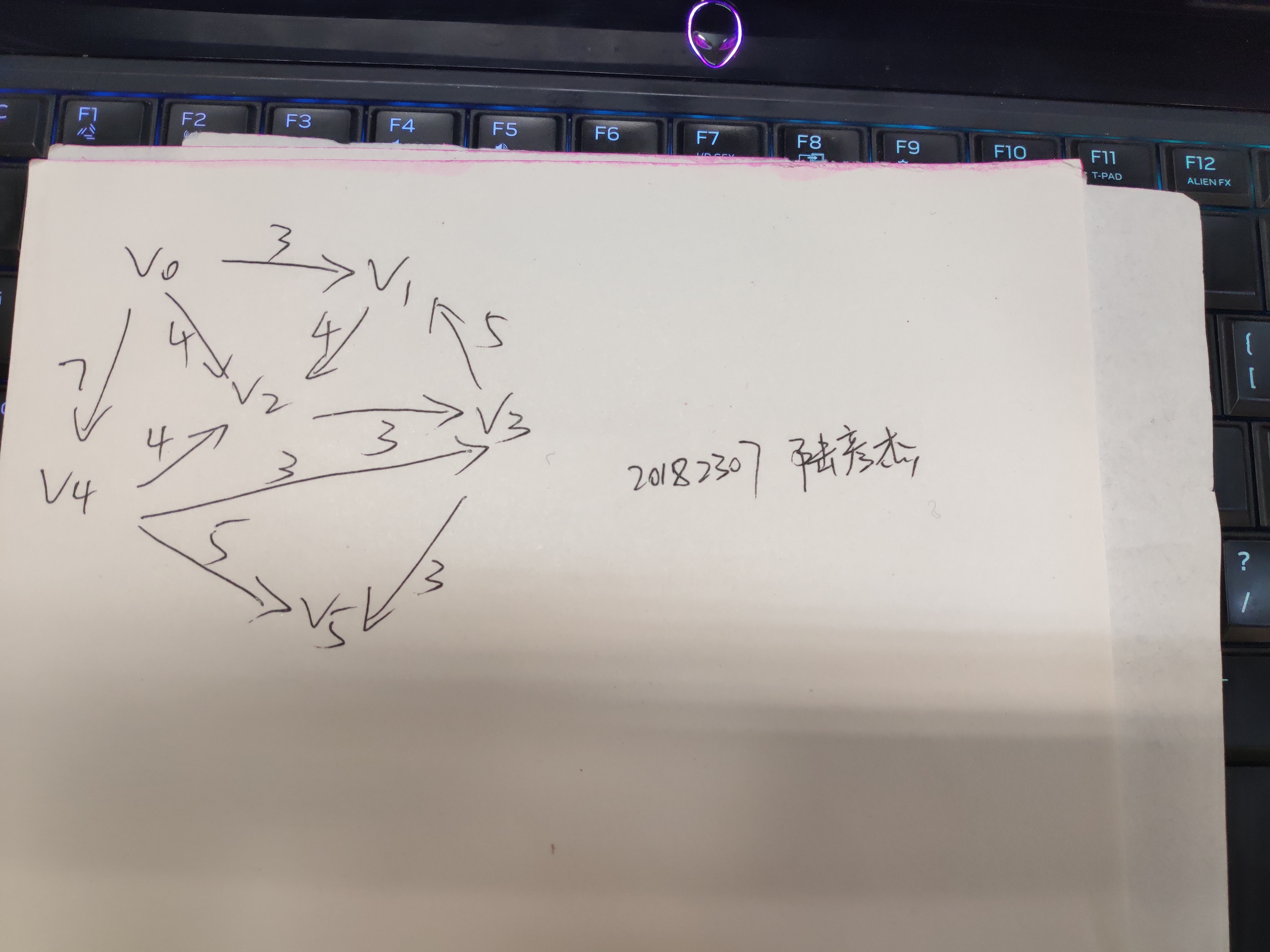
- 将之前课程实践中的提前固定邻接矩阵代码,改为自己输入。关键步骤在于将连接边、设置点的语句中的常量改为变量,通过键盘输入得到。
图的遍历
- 实验目的:将自己所构造的图分别用深度优先遍历与广度优先遍历两种方法遍历一遍
- 实验思路:
- 之前的课程中已经做过深度优先遍历与广度优先遍历的实践练习,这里再描述一次两者的区别与特点:
- 深度遍历的大致实现思路是:把根节点压入栈中。每次从栈中弹出一个元素,搜索所有在它下一级的元素,把这些元素压入栈中。并把这个元素记为它下一级元素的前驱。找到所要找的元素时结束程序。如果遍历整个树还没有找到,结束程序。
- 广度遍历的大致实现思路是:把根节点放到队列的末尾。每次从队列的头部取出一个元素,查看这个元素所有的下一级元素,把它们放到队列的末尾。并把这个元素记为它下一级元素的前驱。找到所要找的元素时结束程序。如果遍历整个树还没有找到,结束程序。
代码示例:
- 之前的课程中已经做过深度优先遍历与广度优先遍历的实践练习,这里再描述一次两者的区别与特点:
//深度优先遍历
public void DFS(String vertexName){
int id=getIdOfVertexName(vertexName);
if(id==-1)return;
vertexs.get(id).setMarked(true);
System.out.print(vertexs.get(id).getName()+" ");
List<Vertex> neighbors = getNeighbors(vertexs.get(id));
for(int i=0;i<neighbors.size();i++){
if(!neighbors.get(i).isMarked()){
DFS(neighbors.get(i).getName());
}
}
}
//广度优先遍历
public void BFS(String vertexName){
int startID=getIdOfVertexName(vertexName);
if(startID==-1) return;
List<Vertex> q=new ArrayList<Vertex>();
q.add(vertexs.get(startID));
vertexs.get(startID).setMarked(true);
while(!q.isEmpty()){
Vertex curVertex=q.get(0);
q.remove(0);
System.out.print(curVertex.getName()+" ");
List<Vertex> neighbors = getNeighbors(curVertex);
for(int i=0;i<neighbors.size();i++){
if(!neighbors.get(i).isMarked()){
neighbors.get(i).setMarked(true);
q.add(neighbors.get(i));
}
}
}
}
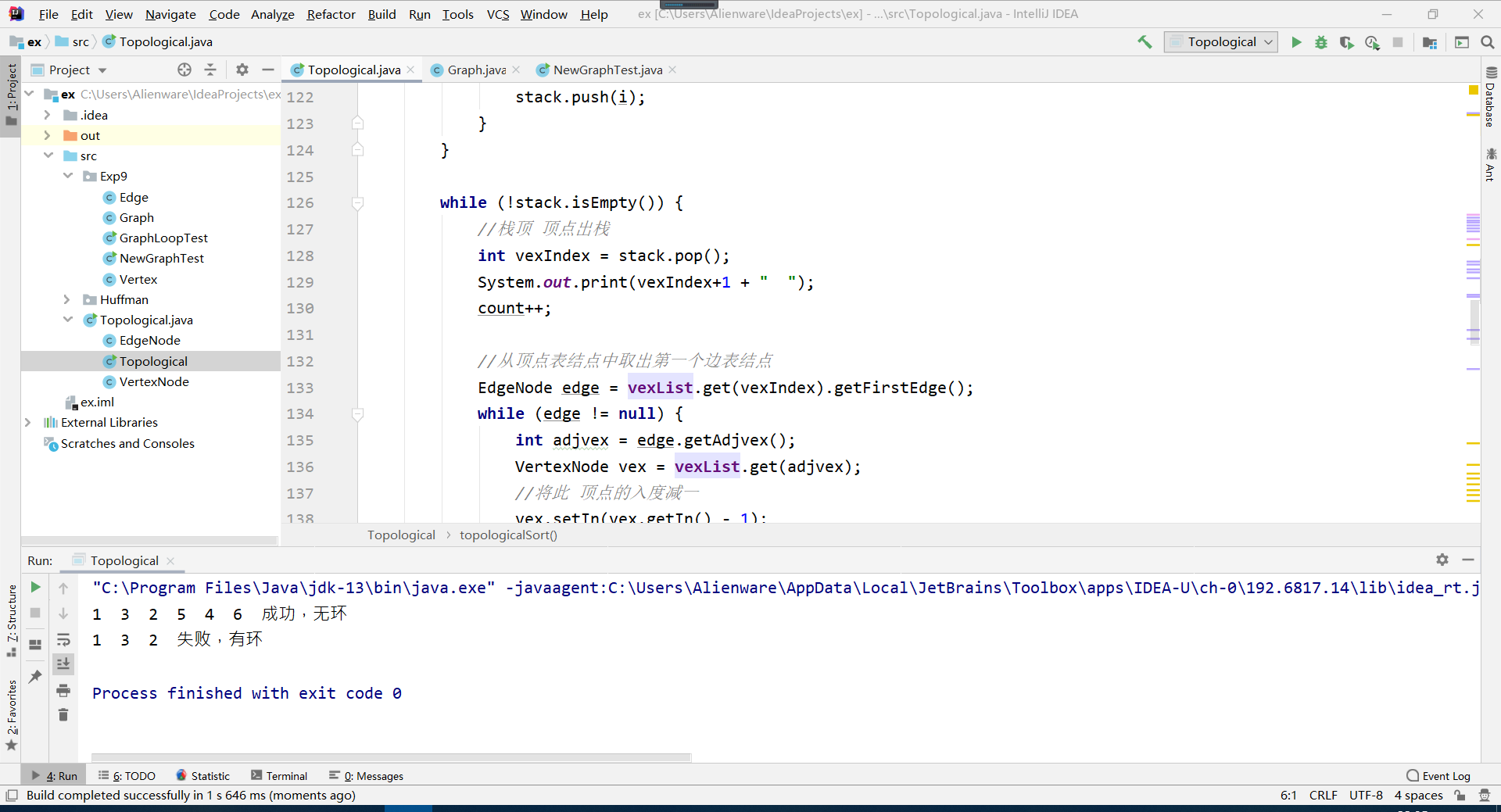
有向图的拓扑排序
- 实验目的:将构建的图进行拓扑排序,并判断是否有环
- 实验思路:
- 拓扑排序的基本思路是:先选定一个入度为零的结点,删除它和它相连的边,将该结点标记为已访问,同时与该结点相连的入度全部减一。接着,重复进行寻找入度为零结点——标记删除——相连结点入度减一的过程,直到所有结点都已被标记或图中有环。
- 运行结果示例:
无向图的最小生成树
- 实验目的:遍历图,用最少的边连接所有的结点
- 实验思路:
- 最小生成树的构造方法共有两种:Kruskal与Prim算法
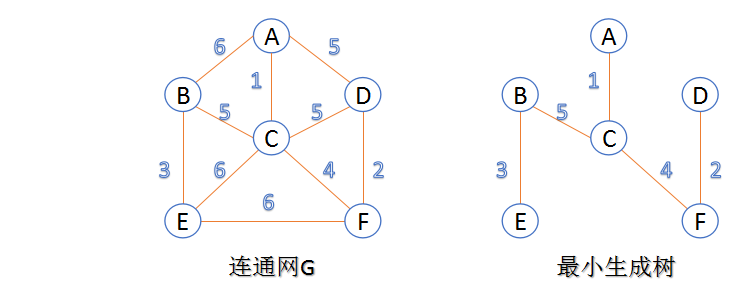
- Kruskal算法基本思路:将权值按从小到大的顺序排列,依次连接,即每一次都连接权值最小的那条边,直到所有结点都在一棵树内或有n-1条边为止
- Prim算法基本思路:从某一特定结点开始,首先选择与其相连的权值最小的边,接着选择与这两个结点相连的权值最小的边,依次进行,每次连接的都是与当前所有结点相连的权值最小的边
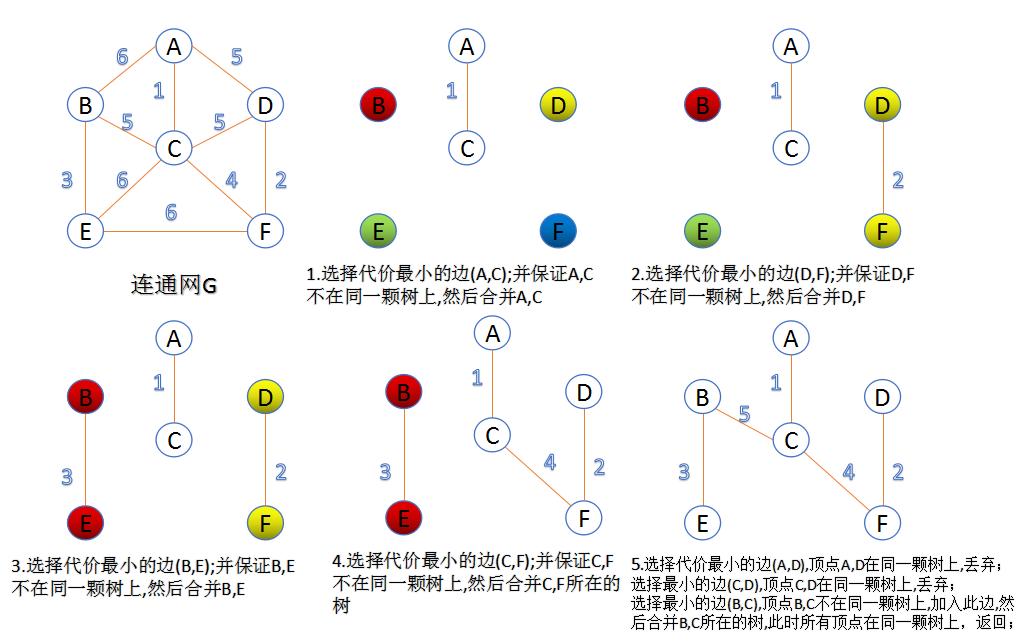
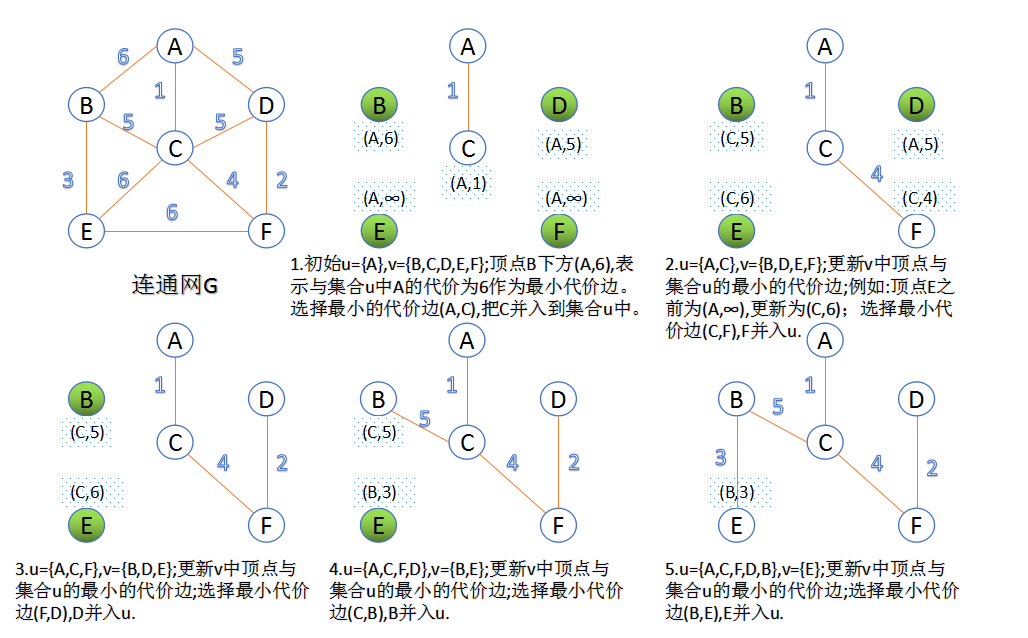
- 最小生成树的构造方法共有两种:Kruskal与Prim算法
最短路径
- 实验目的:利用Dijkstra算法得出图中的最短路径
- 实验思路:
- 最短路径问题研究的是一个结点到其他所有结点的最短路径,Dijkstra算法可得出最短路径的最优解。
- 网络资料:Dijkstra算法之 Java详解
- 详解Dijkstra算法
- 初始时,S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为"起点s到该顶点的距离"[例如,U中顶点v的距离为(s,v)的长度,然后s和v不相邻,则v的距离为∞]
- 从U中选出"距离最短的顶点k",并将顶点k加入到S中;同时,从U中移除顶点k
- 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离
- 重复步骤(2)和(3),直到遍历完所有顶点
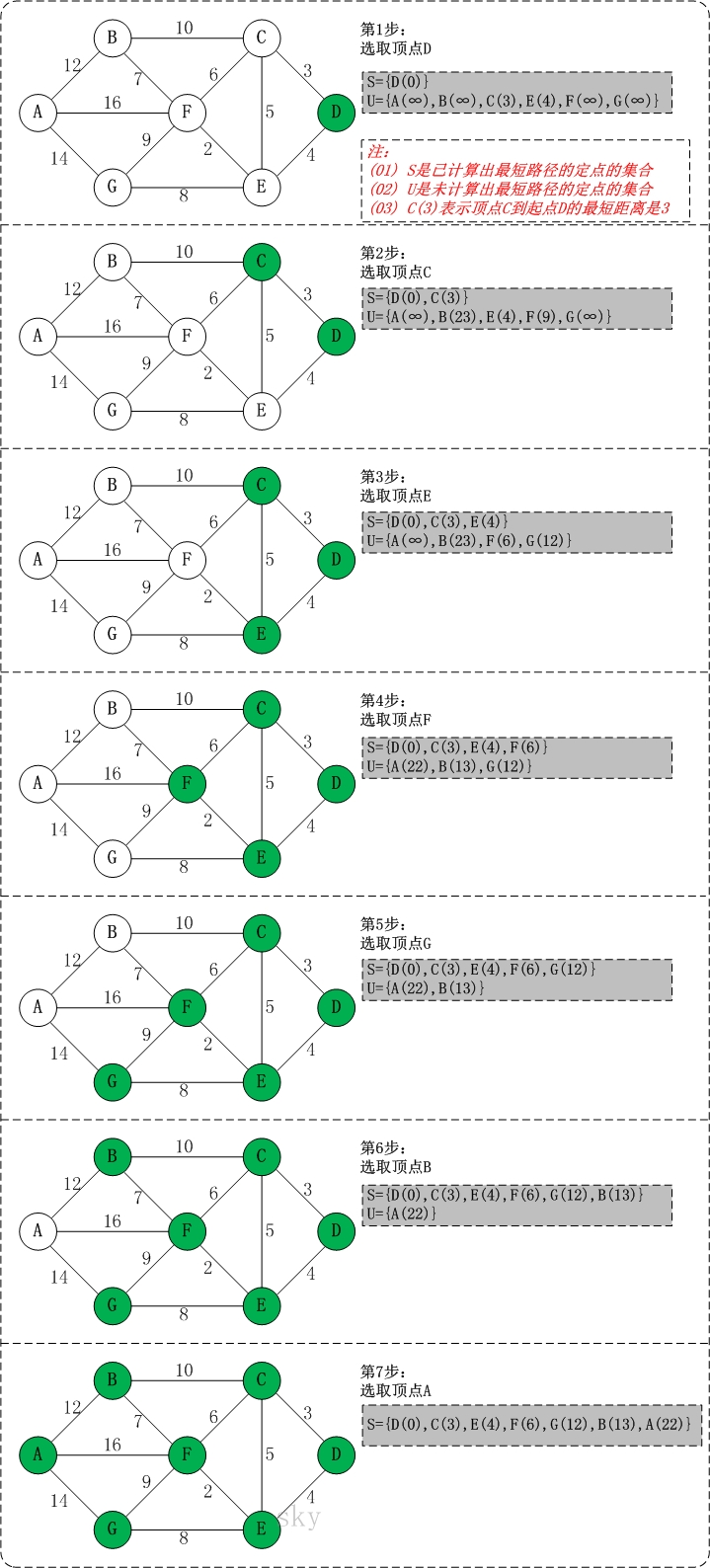
- 最短路径问题研究的是一个结点到其他所有结点的最短路径,Dijkstra算法可得出最短路径的最优解。
最终运行结果图

3. 实验过程中遇到的问题和解决过程
-
问题1:在解决最小路径问题时,程序计算结果为0
-
原因分析:初始化矩阵时,不能直接赋权值为0,不然程序在计算时自然会将0作为最小权值相加

-
解决方案:在初始化矩阵时,将不相连的边的权值赋值为一个极大值

-
-
问题2:实现深度优先遍历算法时,输出的序列与实际的序列是相反的
- 原因分析:由于深度优先遍历主要是通过栈来实现的,所以根据栈“先进后出”的特点,出栈的顺序与真正的遍历顺序是相反的
- 解决方案:使用一个数组,在每一次结点入栈时记录这个结点,最后做一次倒序输出即可
其他(感悟、思考等)
- 图的相关概念由于有之前离散数学的基础,理解掌握起来还是很容易的。但也如前几次实验或实践一样,数据结构的概念掌握与真正的实现之间还是有很大的不同的,需要多加练习,动手实践才能真正领悟学透。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号