20182307 哈夫曼编码实践
20182307 哈夫曼编码实践
任务详情
- 设有字符集:S={a,b,c,d,e,f,g,h,i,j,k,l,m,n.o.p.q,r,s,t,u,v,w,x,y,z}。
- 给定一个包含26个英文字母的文件,统计每个字符出现的概率,根据计算的概率构造一颗哈夫曼树。
- 完成对英文文件的编码和解码。
- 要求:
- 准备一个包含26个英文字母的英文文件(可以不包含标点符号等),统计各个字符的概率
- 构造哈夫曼树
- 对英文文件进行编码,输出一个编码后的文件
- 对编码文件进行解码,输出一个解码后的文件
- 撰写博客记录实验的设计和实现过程,并将源代码传到码云
- 把实验结果截图上传到云班课
实验前的准备及思路构思
- 首先是准备一个包含所有英文字母的文件,然后计算所有字母出现的概率。大致思路是用一个计数变量来给字母计数,然后定义一个数组储存包含26个字母及空格在内的字符的出现概率。初步思路是设计一个双重循环来达成计数与储存的功能。
- 第二是读取和写文件的操作
- 先准备一个文件,读入它的所有内容后将其存入一个足够大的数组,或者根据实际的文本长度自动扩容
- 编码解码时需要生成并写出两个文件,具体代码是
File file = new File("路径\\文件名.txt");
Writer writer = new FileWriter(file);
writer.write(result);
writer.close();
- 代码的大致意思是创建一个新的文件,然后读取这个文件并将编码或解码后的文本存入文件
- 接下来是最重要的构建哈夫曼树的过程,首先要了解哈夫曼树构建的理论过程,参考网络资料:哈夫曼树原理,及构造方法
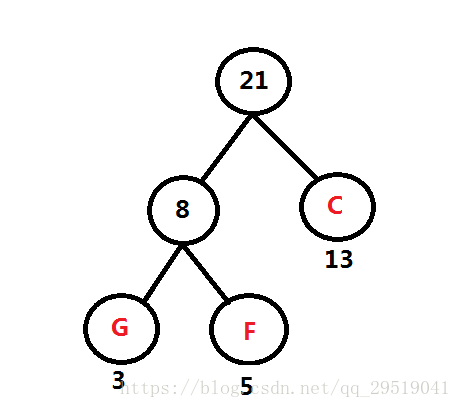
- 编码的思路就是遍历整棵树,当遍历左子树的时候编码加上‘0’,当遍历右子树的时候编码加上‘1’
- 解码时可能需要考虑字符与编码的对应并输出,解决时可能需要两个甚至更多的数组
实验过程
文件读写
- 根据曾经学过的文件读写知识,创建文件并进行读写操作,代码如下:
File file = new File("路径\\文件名.txt");
if(!file.exists()){
file.createNewFile();
}
Reader reader = new FileReader(file);
BufferedReader bufferedReader = new BufferedReader(reader);
String temp = bufferedReader.readLine();
File file2 = new File("路径\\文件名txt");
Writer writer = new FileWriter(file2);
writer.write(result1);
writer.close();
嵌套循环计数
- 两层循环计数并存储:外层循环存储每个字母出现的频率;内层循环遍历文本比较,计数后计算频率
for (int j = 97; j <= 122; j++) {
int number = 0;//给字母计数
for (int m = 0; m < characters.length; m++) {
if (characters[m] == (char) j) {
number++;
}
frequency[j - 97] = (float) number / characters.length;
}
}
构建哈夫曼树
- 哈夫曼树定义:给定n个权值作为n个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
- 构建规则:假设一组权值,一个权值是一个结点,并进行排序,例如:12 34 2 5 7 。在这其中找出两个最小的权值,然后组成一个新的权值,排序。再次找出最小的权值结点。如图:
- 部分代码:
public static HuffNode createTree(List<HuffNode> nodes) {
// 只要nodes数组中有2个以上的节点
while (nodes.size() > 1) {
//进行从大到小的排序
Collections.sort(nodes);
//获取权值最小的两个节点
HuffNode left = nodes.get(nodes.size() - 1);
HuffNode right = nodes.get(nodes.size() - 2);
//生成新节点,新节点的权值为两个子节点的权值之和
HuffNode parent = new HuffNode('无', left.getWeight() + right.getWeight());
//让新节点作为两个权值最小节点的父节点
parent.setLeft(left);
left.setCodenumber("0");
parent.setRight(right);
right.setCodenumber("1");
//删除权值最小的两个节点
nodes.remove(left);
nodes.remove(right);
//将新节点加入到集合中
nodes.add(parent);
}
return nodes.get(0);
}
给每个节点编码
- 遍历整棵哈夫曼树,左子树编码为‘0’,右子树编码为‘1’
- 部分代码:
public static List<HuffNode> breadthFirstTraversal(HuffNode root) {
List<HuffNode> list = new ArrayList<HuffNode>();
Queue<HuffNode> queue = new ArrayDeque<HuffNode>();
//将根元素加入“队列
if (root != null) {
queue.offer(root);
root.getLeft().setCodenumber(root.getCodenumber() + "0");
root.getRight().setCodenumber(root.getCodenumber() + "1");
}
while (!queue.isEmpty()) {
//将该队列的“队尾”元素加入到list中
list.add(queue.peek());
HuffNode node = queue.poll();
//如果左子节点不为null,将它加入到队列
if (node.getLeft() != null) {
queue.offer(node.getLeft());
node.getLeft().setCodenumber(node.getCodenumber() + "0");
}
//如果右子节点不为null,将它加入到队列
if (node.getRight() != null) {
queue.offer(node.getRight());
node.getRight().setCodenumber(node.getCodenumber() + "1");
}
}
return list;
}
输出编码解码文件
- 正常的遍历树,将编码写入文件,再解码,写入一个新的文件
- 解码部分代码:
//将读出的密文存在secretText列表中
List<String> secretText = new ArrayList<String>();
for (int i = 0; i < secretline.length(); i++) {
secretText.add(secretline.charAt(i) + "");
}
//解密
String result2 = "";//最后的解码结果
String current="";// 临时的保存值
while(secretText.size()>0) {
current = current + "" + secretText.get(0);
secretText.remove(0);
for (int p = 0; p < newlist1.size(); p++) {
if (current.equals(newlist1.get(p))) {
result2 = result2 + "" + newlist.get(p);
current="";
}
}
}
实验过程中遇到的问题
-
问题1:程序排序后找出了最小的两个权值,那如何把相加结果的节点添加到树中呢?
- 分析解决:无疑此时需要构造一个全新的节点来成为两个相加节点的代替,具体流程如下:
- 生成新节点,新节点的权值为两个子节点的权值之和
- 让新节点作为两个权值最小节点的父节点
- 删除权值最小的两个节点
- 将新节点加入到集合中
- 分析解决:无疑此时需要构造一个全新的节点来成为两个相加节点的代替,具体流程如下:
-
问题2:如何将节点和编码对应起来并输出?
- 分析解决: 首先构造树的时候就定下了节点的顺序,这时只要按照设计的程序为每个节点编码即可,此时实际已经达成绑定,即一个节点包含的属性有:值,编码;而在最后输出的时候,只需要定义一个列表数组,每个数组元素按遍历顺序获得相应节点的编码并存储,最后输出这个数组即可
- 部分代码:
List<String> newlist1 = new ArrayList<>(); for(int m=0;m < temp1.size();m++) { if(temp1.get(m).getData()!='无') newlist1.add(String.valueOf(temp1.get(m).getCodenumber())); } System.out.println("\n对应编码:"+newlist1);



 浙公网安备 33010602011771号
浙公网安备 33010602011771号