Logistic回归

　　1. logistic回归的基本思想　　

　　logistic回归是一种分类方法，用于两分类问题。其基本思想为：

　　a. 寻找合适的假设函数，即分类函数，用以预测输入数据的判断结果；

　　b. 构造代价函数，即损失函数，用以表示预测的输出结果与训练数据的实际类别之间的偏差；

　　c. 最小化代价函数，从而获取最优的模型参数。

　　2. 逻辑回归的过程

　　逻辑函数（sigmoid函数）：

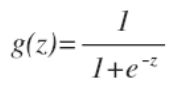
　　该函数的图像：

　　假设函数（分类函数）：

        

 

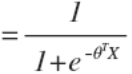
 　　判定边界：

　　 线性边界和非线性边界如下：

　　     

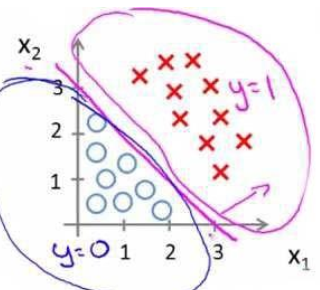
          图1  线性边界                                               图2  非线性边界

线性边界的边界形式：

非线性边界的边界形式可表示为：

　　hθ(x)函数的值表示结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分别为：

                         （概率公式）

　　代价函数为：　

其中：

，

等价于：

代入得到代价函数：

　　这样构建的 Cost(hθ(x),y)函数的特点是：当实际的 y=1 且 hθ 也为 1 时误差为 0，当 y=1 但 hθ 不为 1 时误差随着 hθ 的变小而变大；当实际的 y=0 且 hθ 也为 0 时代价为 0，当 y=0且hθ 不为 0 时误差随着 hθ 的变大而变大。

---

　　实际上，Cost函数和J(θ)函数是基于最大似然估计推导得到的。

　　前面的概率公式可简化为：

　　

　　对应的似然函数为：

　　

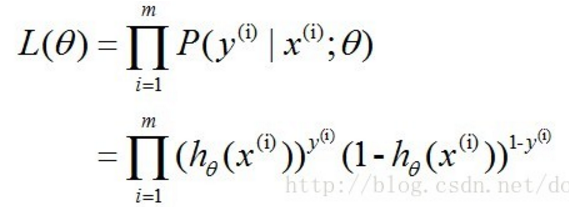
　　对数似然函数为：

　　

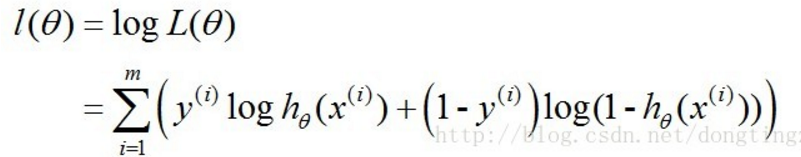
　　最大似然估计就是要求得使l(θ)取最大值时的θ，其实这里可以使用梯度上升法求解，求得的θ就是要求的最佳参数。

  　前面提到的代价函数即可表示为：　

---

梯度下降法求J(θ)的最小值

　　使用梯度下降法求J(θ)的最小值，θ的更新过程：

　　

其中：α学习步长。

　　求偏导：

　　

更新过程可改写为：

α为一常量，所以1/m一般将省略，所以最终的θ更新过程为：

---

　　求解过程中用到如下的公式：

　　

---

 

梯度下降算法的向量化解法：

 　　训练数据的矩阵形式表示如下，其中x的每一行为一条训练样本。

　　

　　参数θ的矩阵形式为：

　　

　　计算x.θ（点乘）并记为A:

 　　

　　求hθ(x)-y并记为E：

　　

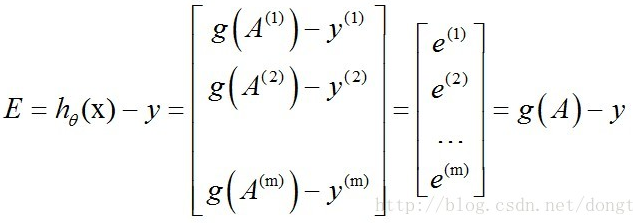
　　g(A)的参数A为一列向量，所以实现g函数时要支持列向量作为参数，并返回列向量。由上式可知hθ(x)-y可以由g(A)-y一次计算求得。

　　θ更新过程，当j=0时：

　　

　　θj同理：

　　

　　综合起来：

　　

　　

　　

　　综上所述，vectorization后θ更新的步骤如下：

　　（1）求A=x.θ；

　　（2）求E=g(A)-y；

　　（3）求θ:=θ-α.x'.E，x'表示矩阵x的转置。

　　也可以综合起来写成：

 　　

 　　

　　正则化逻辑回归：

　　假设函数：

　　

　　梯度下降法最小化该代价函数：

　　

　　参考：

　　1. andrew ng机器学习视频

　　2. http://blog.csdn.net/dongtingzhizi/article/details/15962797