线性回归

1. 一元线性回归

　　假设函数：

　　目标：选择合适的参数和，使得建模误差的平方和最小。即最小化代价函数:

　　　　　　   （其中：m为训练样本的数量）

　　建模误差:预测值和实际值之间的差距。

　　注：代价函数，也可以称之为损失函数。上述代价函数也叫平方误差函数，它是解决回归问题最常用的代价函数。除此之外，还存在其他的代价函数。

　　常用的求解线性回归参数的方法：最小二乘法和梯度下降法

2. 多元线性回归

　　假设函数：  或者 （x0 = 1）

　　也可以简化为：

　　代价函数：

　　最优化参数求解的思路和方法与一元线性回归相同。

　　

注：
1. 数据的归一化处理：使特征具有相近的尺度，帮助梯度下降算法更快的收敛；
2. 学习率：尝试法。
    如果学习率 α 过小，则达到收敛所需的迭代次数会非常高；
    如果学习率 α 过大，每次迭代可能不会减小代价函数，可能会越过局部最小值导致无法收敛。

3. 多项式回归

　　假设函数（以三次方模型为例）：

　　可以使用：

　　

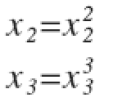
将其转换为线性回归处理。

4. 正则化回归方法

　　正则化方法可以避免模型的过拟合，防止模型过于复杂。

　　（1）岭回归

　　最小二乘估计是最小化残差平方和（RSS）：

岭回归在最小化RSS的计算里加入了一个收缩惩罚项（正则化的l2范数）

 

　　这个惩罚项中lambda大于等于0，是个调整参数。各个待估系数越小则惩罚项越小，因此惩罚项的加入有利于缩减待估参数接近于0。重点在于lambda的确定，可以使用交叉验证或者Cp准则。

　　岭回归优于最小二乘回归的原因在于方差-偏倚选择。随着lambda的增大，模型方差减小而偏倚（轻微的）增加。

　　岭回归的一个缺点：在建模时，同时引入p个预测变量，罚约束项可以收缩这些预测变量的待估系数接近0,但并非恰好是0（除非lambda为无穷大）。这个缺点对于模型精度影响不大，但给模型的解释造成了困难。这个缺点可以由lasso来克服。(所以岭回归虽然减少了模型的复杂度，并没有真正解决变量选择的问题)　

　（2）Lasso回归

lasso是一种相对较新的方法，参考[1],[2]。关于lasso的发展和一些思想介绍可以参考网上很有名气的一篇文章《统计学习那些事》http://cos.name/2011/12/stories-about-statistical-learning/。

lasso是在RSS最小化的计算中加入一个l1范数作为罚约束：

l1范数的好处是当lambda充分大时可以把某些待估系数精确地收缩到0。

关于岭回归和lasso，在[3]里有一张图可以直观的比较（[3]的第三章是个关于本文主题特别好的参考）：

关于岭回归和lasso当然也可以把它们看做一个以RSS为目标函数，以惩罚项为约束的优化问题。

 

 

 

　　（3）elastic net

 

 　　elastic net融合了l1范数和l2范数两种正则化的方法，上面的岭回归和lasso回归都可以看做它的特例：

　　elastic net对于p远大于n,或者严重的多重共线性情况有明显的效果。 对于elastic net，当alpha接近1时，elastic net表现很接近lasso，但去掉了由极端相关引起的退化化或者奇怪的表现。一般来说，elastic net是岭回归和lasso的很好的折中，当alpha从0变化到1，目标函数的稀疏解（系数为0的情况）也从0单调增加到lasso的稀疏解。