计算几何乱写
计算几何
由于计算机中浮点数带有相应的精度误差,故比较大小时要引入一个 \(eps\):
计算几何基本上是围绕向量展开的,而向量可以用一个坐标 \((x, y)\) 表示。接下来我们需要实现向量的基本运算:
-
向量的加减(略)
-
向量的点积(这里用
^表示)当点积为 \(0\),可以判两个向量垂直
\[\begin{align} A\cdot B &= |A||B|cos<A,B> \qquad 其中cos<A, B> 表示 A和B的夹角\\ &= (A_x \overrightarrow x + A_y\overrightarrow y)\cdot(B_x\overrightarrow x+B_y\overrightarrow y) \qquad这里将两个向量按照 xy轴分解 \\ &= A_xB_x(\overrightarrow x \cdot\overrightarrow x) + A_xB_y(\overrightarrow x\cdot \overrightarrow y)\\&\quad +A_yB_x(\overrightarrow y \cdot\overrightarrow x) + |A_y||B_y|(\overrightarrow y\cdot \overrightarrow y)\\ &=A_xB_x + A_yB_y\qquad 根据定义\overrightarrow x\cdot\overrightarrow x = 1,其它同理 \end{align} \]db operator ^ (node A) { return x * A.x + y * A.y; } -
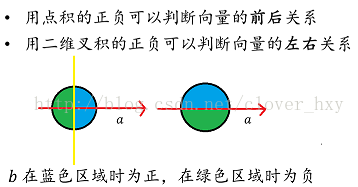
向量的叉积(这里用
*表示)几何意义:\(A\) 转到 \(B\) 所夹平行四边形的有向面积(逆时针为正,顺时针为负)
\(A\times B = |A||B|sin<A, B>\) 推法同理,这里尝试推到更高的三维:
db operator * (node A) { return x * A.y - y * A.x; }
叉积和点积是计算几何中很重要的概念,我们总结一下:
转角公式
逆时针旋转角度 \(B\),原来的向量为 \((cosAr, sinAr)\),现在的向量变为 \((cos(A+B)r, sin(A+B)r) = ((cosAcosB-sinAsinB)r,(sinAcosB+cosAsinB)r)\)
即:\((x,y)\to (xcosB-ysinB,xsinB+ycosB)\)
代码中实现了绕 \(p\) 点逆时针旋转 \(B\) 个弧度,思路是先把 \(p\) 平移到原点转完了再平移回去。
node turn(node p, db B) {
node tmp = (*this) - p;
return p + node(tmp.x * cos(B) - tmp.y * sin(B), tmp.x * sin(B) + tmp.y * cos(B));
}
极角排序
平面上的点和原点连成一条线段,然后用一条在平面上为 \(0\) 度的直线逆时针旋转一直转到 \(360\) 度也就是一圈,这样一个接一个碰到的点就是极角排序的顺序
-
使用
cmath库中的atan2函数(精度损失较大)这是一个给定三角形的对边和邻边算角的函数,返回值是此点与原点连线与 \(x\) 轴正方向的夹角,这样它就可以处理四个象限的任意情况了,它的值域相应的也就是 \(-\pi\sim \pi\)。
对于每个向量求 \(\theta = atan2(y, x)\) 直接排序即可:
bool cmp1(node &A, node &B) { if (atan2(A.y, A.x) != atan2(B.y, B.x)) return atan2(A.y, A.x) < atan2(B.y, B.x); else return A.x < B.x; }还有一种引入了象限来计算:
int quadrant() { if (x > 0 && y >= 0) return 1; if (x <= 0 && y > 0) return 2; if (x < 0 && y <= 0) return 3; if (x >= 0 && y < 0) return 4; return 0; } bool cmp2(node &A, node &B) { if (A.quadrant() == B.quadrant()) return cmp1(A, B); else return A.quadrant() < B.quadrant(); } -
使用叉积(推荐)
叉积 \(=0\) 是指两向量平行(重合);叉积 \(>0\),则向量 \(A\) 在向量 \(B\) 的顺时针方向(\(A\) 在 \(B\) 的下方);叉积\(<0\),则向量 \(A\) 在向量 \(B\) 的逆时针方向(\(A\) 在 \(B\) 的上方)
bool cmp3(node &A, node &B) { node O; // 原点 if (A.quadrant() == B.quadrant()) { if (fabs((A - O) * (B - O)) < eps) return A.x < B.x; // 平行 else return ((A - O) * (B - O) > 0); } else return A.quadrant() < B.quadrant(); }
多边形面积
下面这个公式可以用于凸/凹多边形中。我们可以使用叉积来计算任意多边形的面积,首先将所有点顺时针或者逆时针排序,此时面积等于所有 相邻坐标点与原点构成的向量 的叉积之和 取绝对值除以 \(2\),公式化地 \(S = \dfrac{1}{2}\large\sum\limits_{i = 1}^{n}(x_iy_{i + 1} - x_{i+1}y_i)\) 其中 \(x_{n + 1} = x_1, y_{n+1} = y_1\)。感性理解一下就是把多边形分割成多个三角形,然后进行容斥。(hdu2036)
两直线夹角
若两个向量都是从原点出发,则可以很方便地用 \(θ=atan2(x∗y,x\text^ y)\) 表示,因为叉积是平行四边形,底乘高;点积是底乘投影。于是底就消掉了,可以算出交角。
两直线交点
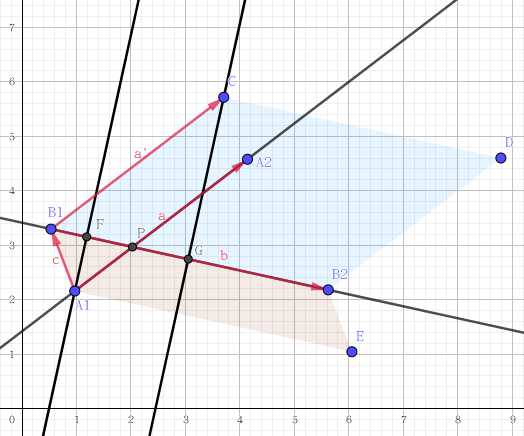
根据上图:首先作一条 \(\overrightarrow{ A_1B_1}\),再由 \(B_1\) 延伸出一条 \(\overrightarrow a\)。则 \(|\overrightarrow a\times \overrightarrow b| : |\overrightarrow c \times \overrightarrow b| = CG:A_1F\),又显然 \(\triangle CGB_1 \sim \triangle FPA_1\),从而有 \(A_1P : |\overrightarrow a| = A_1F : CG\),那么根据 \(P = A_1 + \overrightarrow{A_1P}\),就可以算出 \(P\) 点坐标。
node cross(node A1, node A2, node B1, node B2) {
node A = A2 - A1, B = B2 - B1, C = B1 - A1;
if (A * B == 0) return node(-inf, -inf); // 平行
db t = (B * C) / (B * A);
return A1 + (A * t);
}
判断两条线段是否相交(快速排斥实验 + 跨立实验)
两条线段相交当同时通过快速排斥实验和跨立实验(51nod 1264)
假设两条线段分别为 \(A_1A_2\) 和 \(B_1B_2\)
快速排斥实验:若两线段相交,则以 \(A_1A_2\) 和 \(B_1B_2\) 为对角线分别作两个矩形,那么如果这两个矩形相交,两线段可能相交;如果不相交,则两线段必然不相交。
跨立实验:若 \(A_1A_2\) 跨立 \(B_1B_2\),则向量 \(B_1 - A_1\) 和 \(B_1 - A_2\) 在向量 \(B_2 - B_1\) 两侧,即等价于 \((A_1−B_1)×(A_2−B_1)\) 和 \((A_1−B_2)×(A_2−B_2)\) 不同号,若其中有一个等于 \(0\),说明 \(A_1\) 或 \(A_2\) 在直线 \(B_1B_2\) 上,但是因为已经通过了快速排斥实验,所以这两条线段是相交的,于是这种情况也可以;同理,若 \(B_1B_2\) 跨立 \(A_1A_2\),\((B_1−1_1)×(B_2−A_1)\) 和 \((B_1−A_2)×(B_2−A_2)\) 不同号或其中一个等于 \(0\)。当且仅当 \(A_1A_2\) 跨立 \(B_1B_2\) 且 \(B_1B_2\) 跨立 \(A_1A_2\),跨立实验成功。
bool intersect(line a, line b) {
// 快速排斥实验
if (min(a.p.x, a.q.x) > max(b.p.x, b.q.x) || min(a.p.y, a.q.y) > max(b.p.y, b.q.y) ||
min(b.p.x, b.q.x) > max(a.p.x, a.q.x) || min(b.p.y, b.q.y) > max(a.p.y, a.q.y))
return false;
// 跨立实验
return ((orient(b.p, a.p, a.q) * orient(b.q, a.p, a.q) <= eps) &&
(orient(a.p, b.p, b.q) * orient(a.q, b.p, b.q) <= eps));
}
判断一个点是否在多边形内
首先引入两个函数分别判断一个点是否在直线和线段上(利用叉积和点积):
bool on_line(line a, node b) {
return fabs(orient(b, a.p, a.q)) < eps;
}
bool on_segment(line a, node b) {
return on_line(a, b) && ((a.p - b) ^ (a.q - b)) <= eps;
}
考虑 \(O(n)\) 的 射线法,虽然相对于二分法的时间效率较慢,但是射线法适用于任何多边形的判断:射线法就是选取多边形外一点和所需判断的点连成一条线,若该直线和多边形的交点个数为奇数,则该点在多边形内,否则,该点在多边形之外。原理是在每碰到一条边,内外的状态就会改变一次。
然而,我们还要特殊考虑射线恰好交在一个点上或者是射线与一条边重合的情况:
- 若交于一点,我们考虑将每条线段设为下开上闭的区间,即射线交到下面的端点则不算,其余部分才算
- 若与边重合,则忽略这条边
bool in_polygon(node *a, node b, int n) {
bool ret = false; node sd(-inf, b.y); // 射线的另一个端点
for (int i = 1; i <= n; i++) // 恰好在边上
if (on_segment(line(a[i], a[(i % n) + 1]), b))
return true;
for (int i = 1; i <= n; i++) {
if (fabs(a[i].y - a[(i % n) + 1].y) < eps) continue; // 边重合
if (b.y > min(a[i].y, a[(i % n) + 1].y) && b.y <= max(a[i].y, a[(i % n) + 1].y))
if (intersect(line(sd, b), line(a[i], a[(i % n) + 1])))
ret = !ret;
// 上面三行实现了下开上闭区间的判断 和 射线与边相交的判断
}
return ret;
}
还有 \(O(logn)\) 的二分法,把凸包分成以 \(p_1\) 为顶点的 \(n-2\) 个三角形,判断是否有一个三角形把所要判断的点包住(poj1264):
bool in_convexhull(node *a, node b, int n) {
int lb = 2, ub = n; // [2, n)
while (lb < ub) {
int mid = (lb + ub) >> 1;
db x1 = orient(a[1], a[mid], b), x2 = orient(a[1], a[mid + 1], b);
if (x1 >= 0 && x2 <= 0) { // points are anticlockwise
if (orient(a[mid], a[mid + 1], b) >= 0) return true;
else return false;
}
if (x1 >= 0) lb = mid + 1;
else ub = mid;
}
return false;
}
凸包(Graham 扫描法 和 Andrew 算法)
Andrew 算法 是 Graham 扫描法 的一种变体,常数小一些。
先介绍 Graham 扫描法:
① 找一个一定在凸包上的点 \(P1\)(一般找纵坐标最小的点);
② 将其余所有的点以 \(P1\) 为基准进行极角排序;
③ 从 \(P1\) 出发扫描所有的排序好的点(逆时针顺序),不断地更新凸包最外围的点,是否在最外围可由叉乘判断,
当前对点 \(P\) 进行判断,\(P_1,P_2\) 为前面加入的两个点:
- 若点 \(P\) 在内部(图一)则有向量 \(a\) 叉乘向量 \(b\) 大于零,此时点 \(P\) 是凸包的顶点,应直接将 \(P\) 点加入凸包。
- 若在点 \(P\) 在外部(图二),则有向量 \(a\) 叉乘向量 \(b\) 小于等于零,若直接加入 \(P\) 就会破坏凸包的凸性,那么此时应该将点 \(P_1\) 舍弃,继续对前两个点进行判断,直到 \(P,P_1,P_2\) 三个点满足向量 \(a\) 叉乘向量 \(b\) 大于零,再将 \(P\) 点加入凸包。
Andrew 算法 的具体流程是:
① 将所有的点按照横坐标从小到大进行排序,横坐标相同则按纵坐标从小到大排;
② 将 \(P[1]\) 和 \(P[2]\) 加入凸包,然后从 \(P[3]\) 开始判断,判断方式同 Graham 扫描法 中一致;
③ 将所有的点扫描一遍以后,我们便可以得到一个下凸包(横坐标不会减小);
④ 同理,我们从 \(P[n-1]\) 开始(\(P[n]\) 已经判过了),反着扫描一遍,便可以得到一个上凸包;
⑤ 将两个半凸包合在一起就是一个完整的凸包,注意的是由于起点 \(P[1]\) 在正着扫描和反着扫描时都会将其加入凸包,故需要将最后一个点(\(P[1]\))去掉才为最终结果。
旋转卡壳
这个算法可以用来求凸包直径,即凸包最远点对的距离。
先用动图来直观理解一下这个概念:
我们依次枚举凸包上的每一条边,计算一下哪个点到他的距离最远,然后计算一下距离,根据凸包的凸性可知随着边逆时针枚举,所对应的点也是逆时针出现的。接下来就剩下一个小问题:怎么判断当前的距离是否更大?考虑使用叉积,因为边的长度是固定的,如果距离越远,那么,边和点连成的面积也就越大。
db rotate_caliper(node *a, int n) {
if (n == 2) return line(a[1], a[2]).len();
db ret = 0;
for (int i = 1, j = 2; i <= n; i++) {
while (orient(a[i], a[(i % n) + 1], a[j]) <= orient(a[i], a[(i % n) + 1], a[(j % n) + 1]))
j = (j % n) + 1;
ret = max(ret, max(line(a[i], a[j]).len(), line(a[(i % n) + 1], a[j]).len()));
}
return ret;
}
半平面交
一条直线可以把平面分为两部分,其中一半的平面就叫半平面,那么半平面交,就是多个半平面的相交部分。
半平面交有什么用?可以求解一个区域,可以看到给定图形的各个角落(多边形的核) 和 求可以放进多边形的圆的最大半径
算法的具体步骤如下:
-
选取一个正方向,一般来说是逆时针,将所有边按逆时针方向作为有向线段,这样选取的好处是保证核在有向线段的左边。与此同时,把有向线段进行极角排序
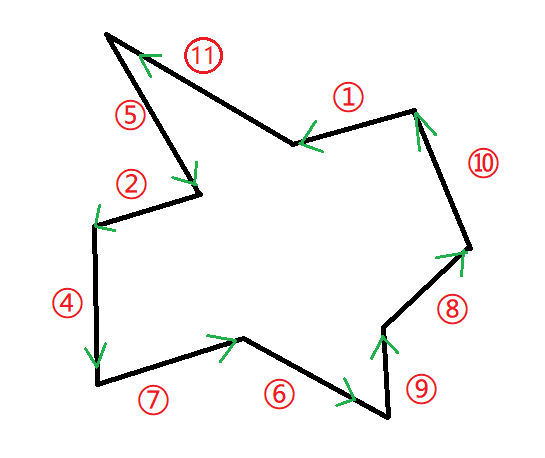
-
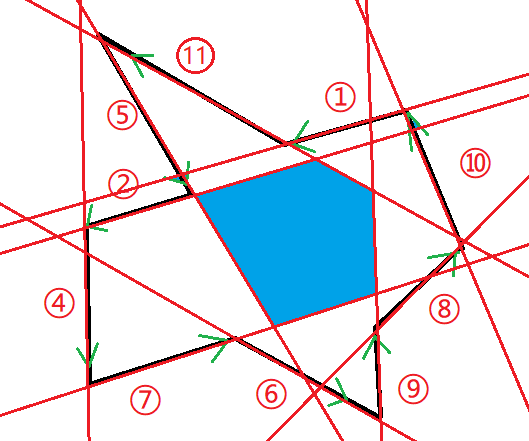
按顺序遍历每一条线段,取左边的区域,删除右边的区域,这里使用图示演示一下这个过程:
\(\cdots\cdots\)
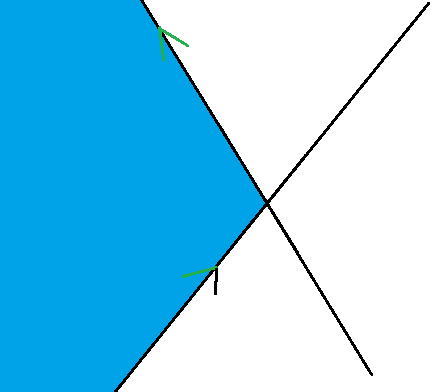
我们考虑使用双端队列来维护半平面交:
在下图中,蓝色为当前半平面交。
当我们加入红色线段时,半平面交产生了变化。
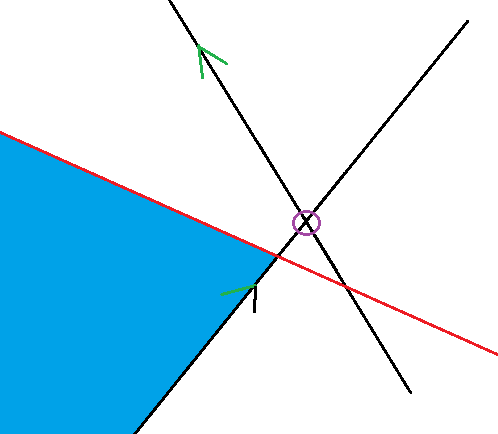
因为我们对线段进行了排序,所以加入的线段会比前面的更“陡”。显然,如果先前的两条线段的交点在当前加入线段的右侧,则较“陡”的那条线段就会无效。
注意:本算法中的左侧右侧是相对的,不是绝对的。这里是相对于逆时针线段而言的
闵可夫斯基和
定义平面上两个图形 \(A,B\) 的闵可夫斯基和为 \(C = \{a + b|a\in A, b\in B \}\)
假设 \(A, B\) 都是凸集,那么我们现在思考 \(A, B\) 闵可夫斯基和的性质。
我们来证明第一个性质,闵可夫斯基和 \(AB\) 也是一个凸集:
我们知道凸集的充要条件是任意两点的连线上所有点都属于该集合,即若 \(a,b \in A\),则 \(xa+(1-x)b\in A\)。
假设 \(a_1, a_2\in A\),\(b_1, b_2\in B\),那么对于任意 \(x\),有 \((a_1 + b_1)x +(a_2 + b_2)(1- x) = \big(a_1x+a_2(1-x) \big) + \big(b_1x + b_2(1-x) \big) \in AB\)。
可以发现后面两个项一个属于 \(A\),另一个属于 \(B\),那么它们的和属于闵可夫斯基和。那么前面那个式子也属于闵可夫斯基和,根据凸集的充要条件可知:两个凸集的闵可夫斯基和也是个凸集。
第二个性质是一条出现在 \(A\) 凸包上的边,也一定出现在闵可夫斯基和的凸包上:
这个比较好证明,我们直接拿 \(A\) 集合一条边的方向,去集合 \(B\) 中找该方向上最外侧的点,因为一个点作为凸包边的条件是在该点外侧无更多点,那么此时 \(A\) 集合的这条边和 \(B\) 集合中找出的点已经为最大了,无更多点。
那么求法就简单了,把两凸包的边极角排序后直接顺次连起来就是闵可夫斯基和,由于凸包的优美性质,这里直接归并排序。但是需要注意的是可能会有三点共线的情况,于是重新求一次凸包就好了。
具体代码见洛谷P4557 战争。
自适应辛普森法
求解积分数值的方法。设 \(f(x)\) 为原函数,\(g(x) = Ax^2+Bx+C\) 为拟合后的函数,则有
于是得到了 Simpson 公式,如下:
在计算机中,我们还要注意答案的精度,区间分少了精度可能不够,区间分多了又会太慢,自动控制区间分割的大小,就是自适应辛普森法的好处。实现很简单,就是二分递归的过程,如果满足了精度需要,则可以终止递归。
圆的反演
先进行直观理解:见音频库中”圆的反演”
设反演中心为 \(O\),反演半径为 \(R\)(其实可以看做关于圆心为 \(O\) 半径为 \(R\) 的圆进行反演)。若经过 \(O\) 的直线过 \(P,P′\),且 \(OP\times OP′=R^2\),则称 \(P,P′\) 关于 \(O\) 互为反演。反象是指反演变换后的图形。
反演有几个重要的性质:
-
除反演中心外,平面上的每一个点都只有唯一的反演点,且这种关系是对称的,位于反演圆上的点,其反演保持在原处;位于反演圆外部的点,反演为圆内部的点;位于反演圆内部的点,反演为圆外部的点。
举个例子:\((0, 1]\) 以 \(1\) 为反演点,则结果为 \([1, +\infty)\),这就是一维反演。
-
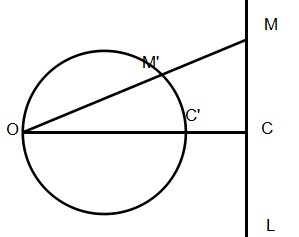
任意一条不过反演中心的直线,它的反形是经过反演中心的圆,反之亦然。推广来说,过反演中心相交的圆,变为不过反演中心的相交直线。证明如下,对于下面这个图,根据 \(ΔOM′C′\sim ΔOCM\),容易得到\(|OM|\times|OM′|=|OC|\times|OC′|\),因此 \(C', C\) 和 \(M', M\) 为反演点对。
-
不过反演中心的圆,反形也为不过反演中心的圆,并且反演中心为这两个互为反形的圆的位似中心(不仅是相似图形,而且每组对应点的连线交于一点)。\(O\) 为反演中心,\(A\) 和 \(A'\),\(B\) 和 \(B'\) 都是互为反演点。
-
相切两圆的反象仍相切,若切点恰是反演中心,则其反象为两平行线。另外可以推出,相离的两圆反演(反演中心不在圆上)后仍然相离;两圆相切,若反演中心只在其中的一个圆上,则为反形为相切的直线与圆。
圆的反演之所以很美妙且很实用,在于反演不改变相切关系。
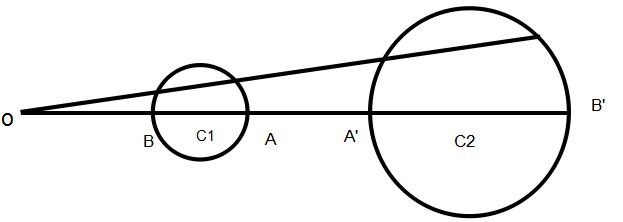
在解题过程中,对于一个不过反演中心的圆,怎样求它的反形圆?我们分别求出反形的圆心和半径即可。
这里我们拿上面那张图作为例子,先求反形的半径,容易有:
设 \(O\) 点坐标为 \((x_0,y_0)\),\(C_1\) 坐标 \((x_1, y_1)\),\(C_2\) 坐标 \((x, y)\),则有:
1、ZOJP1608Two Circles and a Rectangle
先是要保证最大圆的直径要大于等于矩形最短的边长,否则放不进去。
考虑极限情况,即两个圆的边相切且处于对角状态。此时两圆圆心距离\(z=r_1+r_2\),两圆横坐标的距离\(x=a-r_1-r_2\),纵坐标距离\(y=b-r_1-r_2\)。当极限情况时,以\(x、y、z\)三边组成的三角形显然为直角三角形,即\(z^2=x^2+y^2\)。因为\(z\)不变,若两圆之间有间距\(x\)和\(y\)都会变大,显然此时\(z^2<x^2+y^2\)。
综上,当\(z^2>x^2+y^2\)时,容不下两个圆。
2、洛谷P3829 信用卡凸包
这道题要学会转化题意,转化为关于凸包的问题:
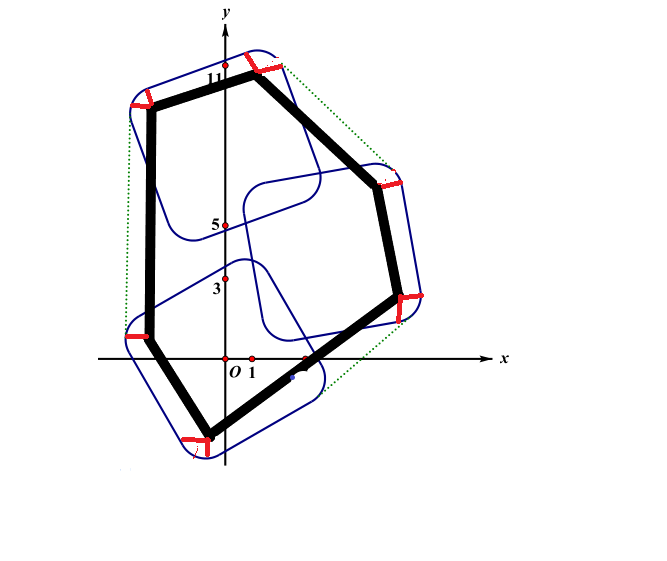
我们容易发现,只要将每个转角对应的点的凸包先计算出来,再根据多边形的外角和为 \(360°\),总共圆弧的部分加起来也相当于一个圆的周长,因此凸包周长加上一个圆的周长即为信用卡凸包的周长。
3、洛谷P3187 最小矩形覆盖
经典的旋转卡壳求矩形覆盖问题,我们可以同时卡三个点,一个是最上面的点(显然用叉积判断),另外两个分别为最左和最右两个点(不妨使用点积判断)。本题的难点在于如何求出矩形的四个顶点,我们只要求出当前边的向量,就可以推出与其垂直的向量,然后可以根据 卡的三个点 和 这些点加上对应的向量 确定矩形边所在的直线,使用直线交点模板求出顶点即可。
4、洛谷P3194 水平可见直线
半平面交,将所有直线按照斜率从小到大排序,若栈顶和次栈顶直线的交点在当前直线的右侧,则栈顶不可见,弹出。本题构造结束后栈里所有直线并不构成多边形,因此不需要拿头和尾连在一起判是否需要弹掉。不过本题似乎卡精度,使用 \(atan2\) 函数会 WA
5、洛谷P4557 战争
闵可夫斯基和 好题
如果以向量 \(\overrightarrow p\) 移动 \(B\) 凸包能够与 \(A\) 凸包相交,构造闵可夫斯基和 \(C=\{A+(-B)\}\),那么 \(\overrightarrow p\) 必属于 \(C\)。在输入 \(B\) 时把所有坐标都取反即可。
6、洛谷P4207 月下柠檬树
容易发现,经过投影后原树的树长变为 \(cot\alpha\) 倍。于是,题目就是要求如下图的面积并:
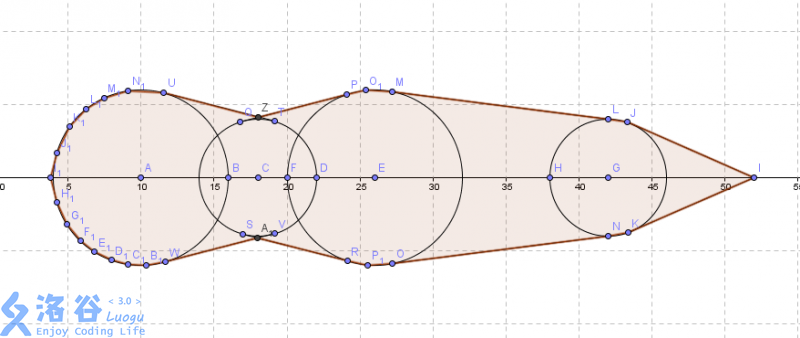
这种求面积并的一般做法就是使用自适应辛普森积分,我们只要能够求出一半的图像面积,于是函数 \(f(x)\) 即是 \(x\) 上最大的纵坐标值。有两种情况:一种是圆周上,另一种是相邻两圆的切线上。切线求法是由圆心向切线作垂线,再由垂足向 \(x\) 轴作垂线,很容易求出两条辅助线相交的角的三角函数值,从而确定这条切线。
7、hdu 4773
圆的反演经典例题,题意:给定相离的两个圆,在这两个圆外给定一个点 \(P\),求符合条件:过点 \(P\) 的圆且与已知的两个圆外切的所有圆的总数和它们的圆心坐标和半径。
先以点 \(P\) 为为反演中心,反演半径随便设置都可以,为了计算方便就设为 \(1\),把圆 \(C_1\) 和圆 \(C_2\) 反演后再求这两个圆的公切线,再把这个公切线反演回去,那么就是一个过点 \(P\) 的圆,且与原来的 \(C_1\) 和 \(C_2\) 相切。
8、codeforces 372E Drawing circles is fun
考虑两组点是否符合要求 \((p_1, p_2)(p_3, p_4)\),那么将构成的四个圆对于 \(O\) 进行反演,就会得到一个平行四边形,而平行四边的充要条件有一个是两对角线交于中点,于是只要把所有对角线求出来,然后将中点一样却斜率不同的方案组合算出来,加起来即可。