Burnside引理和Polya定理

群的定义：

设 \(G\) 是一个集合，\(∗\) 是 \(G\) 上的二元运算，若 \((G,∗)\) 满足下面的条件：则称 \((G,∗)\) 为一个群。
① 封闭性：\(∀a,b∈G，a∗b∈G\)
② 结合律：\(∀a,b,c∈G，(a∗b)∗c=a∗(b∗c)\)
③ 单位元：\(∀a∈G，∃e∈G，a∗e=e * a = a\)
④ 逆元：\(∀a∈G，∃a′∈G，a∗a′=e\)

若群中的元满足交换律，则该群被称作为阿贝尔群。

置换的定义：

设 \(X\) 是一个有限集，\(π\) 是 \(X\) 到 \(X\) 的排列的一个变换且为双射，则称 \(π\) 是 \(X\) 上的一个置换。

可将一个\(\{1,2,3,\cdots,n\}\) 的置换 \(π\) 记为：

\[\pi=\begin{pmatrix} 1 & 2 & \cdots & n\\ a_1 & a_2 & \cdots & a_n\\ \end{pmatrix} \]

注意：① \(π\) 是集合的运算；② 置换不是针对下标，而是针对集合中的元素。也就是说，\(π\) 的第一行不一定是\(\{1,2,3,\cdots,n\}\)；③同一置换用这样的表示法有 \(n!\) 种，但其对应的关系不变。

接下来就是用循环节表示置换的第二种置换的表示方法。设

\[\pi=\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 2 & 4 & 5 & 1 & 3 & 6\\ \end{pmatrix}\\ \]

它也可以唯一的表示为 \(π=(1~2~4)(3~5)(6)\)，每一个括号内表示一个循环，这个置换有 \(3\) 个循环节。
置换间也有二元运算，运算符为 ”\(·\)“。

这里补充一下满射、单射、双射的概念：

单射就是只能一对一，不能多对一；满射只要 \(Y\) 中的元素在 \(X\) 中都能找到原像就行了（一对一，多对一都行）；双射就是既是单射又是满射（一个对一个,每个都不漏掉）

置换群：

设 \(G\) 为有限集 \(X\) 上的置换的集合，若 \(G\) 满足群的定义，则 \((G，⋅)\) 被称为一个置换群。

对于元素 \(a,b∈X\)，若 \(∃π∈G\)，\(π(a)=b\)，则称 \(a\) 与 \(b\) 是等价的，记为 \(a\sim b\)。
注意：① \(a,b\) 是 \(X\) 的单一的元，不是一个有限集；② \(π(i)\) 表示 \(π\) 中 \(i\) 的对应关系，而不是集合的一个置换。

\(X\) 的元素形成的等价类称为 \(G\) 的轨道，任意两条轨道不相交，等价类的个数记为 \(L\)。

\(Z_k\)（\(K\) 不动置换类）：设 \(G\) 是 \(1\sim n\) 的置换群。若 \(K\) 是 \(1\sim n\) 中某个元素，\(G\) 中使 \(K\) 保持不变的置换的全体，记作 \(Z_k\)，叫做 \(G\) 中使 \(K\) 保持不动的置换类，简称 \(K\) 不动置换类。

\(E_k\)（等价类）：设 \(G\) 是 \(1\sim n\) 的置换群。若 \(K\) 是 \(1\sim n\) 中某个元素，\(K\) 在 \(G\) 作用下的轨迹，记作 \(E_k\)。即 \(K\) 在 \(G\) 的作用下所能变化成的所有元素的集合。

轨道-稳定集定理：\(|E_k||Z_k| = |G|\quad \quad k=1,2,\cdots.n\)

证明：设 \(|E_k| = L\)，\(E_k = \{a_1(=k),a_2,\cdots,a_L \}\)

由 \(E_k\) 的定义可知，存在置换 \(p_i \in G\)，使得 \(p_i(a_1) = a_i\quad \quad i = 1, 2, \cdots, L\)

令 \(Z_kp_j = \{\pi\cdot p_j|\pi\in Z_k \}\quad\quad j = 1, 2, \cdots, L\)

首先由于 \(\pi_1\neq\pi_2\)，可得 \(p_j\pi_1\neq p_j\pi_2\)，故 \(|Z_kp_j| = |Z_k|\)。然后，显然有 \(Z_kp_1\bigcup Z_kp_2\bigcup \cdots\bigcup Z_kp_L \subseteq G\)。任取置换 \(p\in G\)，若 \(p(a_1) = a_j\)，则 \(a_j\) 与 \(a_1(= k)\) 等价，故 \(a_j\in E_k\)。由 \(pp_j^{-1}(a_1) = p_j^{-1}(p(a_1)) = p_j^{-1}(a_j) = a_1\)，知 \(pp_j^{-1}\in Z_k \implies p\in Z_kp_j\)，所以 \(G\subseteq Z_kp_1\bigcup Z_kp_2\bigcup \cdots \bigcup Z_kp_L\)

因此 \(G = Z_kp_1\bigcup Z_kp_2\bigcup \cdots \bigcup Z_kp_L\)，\(|G| = |Z_kp_1| + |Z_kp_2| + \cdots + |Z_kp_L| = L\cdot|Z_k| = |E_k||Z_k|\)

（简单来说就是每个稳定集的元素都有大小为 \(|E_k|\) 的循环节）

Burnside 引理：\(L\) 表示等价类的个数，\(C(\pi)\) 表示置换 \(\pi\) 作用下不变的元素的个数

\[L = \frac{1}{|G|}\sum_{i = 1}^{n}|Z_i| = \frac{1}{|G|}\sum_{\pi\in G}C(\pi) \]

证明：

根据 \(C(\pi)\) 的定义，易知：\(\sum\limits_{i= 1}^n|Z_i|=\sum\limits_{\pi\in G}|C(\pi)|\)
根据轨道-稳定集定理，可知 \(|E_i||Z_i| = |G|\)，所以可知：

\[\begin{align} \sum\limits_{\pi \in G}C(\pi) &= \sum\limits_{i = 1}^n|Z_i| = |G|\sum\limits_{i = 1}^n\frac{1}{|E_i|} = |G|\sum_{i = 1}^{L}1\\ &= L\cdot|G|\\ &\therefore L = \frac{1}{|G|}\sum_{\pi\in G}C(\pi) \end{align} \]

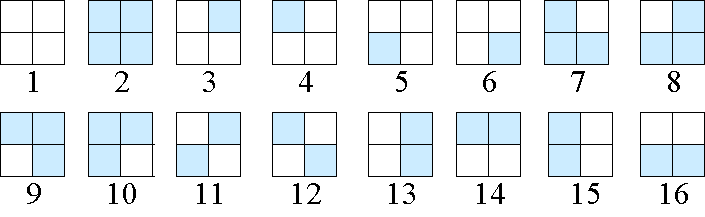
例题：\(4\) 个相同格子，用白蓝两种颜色着色，有多少种不同的方案？经过旋转 \(90°\) 或 \(180°\) 后相同的方案算同一种。

要求不同的涂色方案，我们可以把所有的涂色方案求出来，编号 \(1,2,\cdots,16\)（如图所示）。
然后把 \(\{①不转，②顺时针转90°，③转180°，④顺时针270°\}\) 作为置换群，求等价类的个数。

分类讨论：
① 不转：置换可以表示为 \((1)(2)\cdots(16)\)；
② 顺时针转 \(90°\)：\((1)(2)(6 ~5~ 4~ 3)(10~ 9~ 8~ 7)(11~ 12)(16~ 15 ~14~ 13)\)；
③ 转 \(180°\)：\((1)(2)(3~ 5)(4~ 6)(7~ 9)(8 ~10)(11)(12)(13~ 15)(14 ~16)\)；
④ 转 \(270°\)：\((1)(2)(3~ 4~ 5~ 6)(7~ 8~ 9~ 10)(11 ~12)(13~ 14~ 15~ 16)\)；

所以不等价类为 \(\large{\frac{16+2+4+2}{4}}=\small6\) 种。

Polya 定理：设 \(G=\{π_1，π_2，π_3,\cdots,π_p \}\) 是 \(X=\{a_1，a_2，a_3,\cdots,a_n\}\) 上的一个置换群，用 \(m\) 种颜色对 \(X\) 中的元素进行涂色，那么不同的涂色方案数为（\(c(\pi_k)\) 为置换 \(\pi_k\) 的循环节的个数，注意 \(c\) 区分大小写）：

\[L=\frac{1}{|G|}\sum_{\pi\in G}m^{c(\pi)} \]

设 \(G'=\{π'_i~|i∈[1,p]\}\) 是作用在图像上的 \(X=\{1,2,...,m^n\}\)（共有 \(m^n\) 种染色方案）的置换群。

由Burnside 引理知：

\[L=\frac{1}{|G'|}\sum_{i = 1}^{p}C(π'_i) \]

要证明的结果为：

\[L=\frac{1}{|G|}\sum_{i = 1}^{p}m^{c(\pi_i)} \]

对比 Burnside 定理 只要证明 \(m^{c(\pi_i)} = C(\pi'_i)\)。\(C(\pi'_i)\) 表示置换中不变的元素个数，而在 \(π_i\)中，若使得元素不变，每一个循环节内的颜色必须相同，因为每个循环节可以染 \(m\) 种颜色，又有 \(c(π_i)\) 个循环节，所以即为\(m^{c(π_i)}\)种情况。

总结一下：Burnside 引理首先要找到所有的情况，然后置换群作用在情况上，找出等价类；Polya 定理并不需要列举出所有的情况，直接用置换群作用在染色方案上，找出不同的染色方案。

最近学校里学了同分异构体的概念，目前找到一篇文章 https://blog.csdn.net/qq_35950004/article/details/105228566
有空学一下。