IMOSL2019 C3~C9
(如果文中有伪证,请联系我)
C3
有一个很妙的做法。考虑把整个过程倒过来看。一开始,有一个指针在位置 \(0\),所有硬币都是 T。每次,
- 可以把指针右移一位,使得移动后的指针指向一个
T,之后要把这个T变为H - 可以把指针左移一位,使得移动后的指针指向一个
H,之后要把这个H变为T
考虑左移 / 右移操作形成的连续段,设它们的长度形成的序列为 \(a_1,a_2,\cdots,a_k\)。那么 \(a\) 需要满足
设所有可能的序列形成集合 \(A\),所有可能的硬币初始状态形成集合 \(B\)。
对于一个序列 \(a\),设它对应的硬币初始状态为 \(f(a)\)。需要证明 \(\forall a^0\ne a^1\),\(f(a^0)\ne f(a^1)\)。可以找到 \(a^0,a^1\) 的最长公共前缀 \(a_{1..i}\),则 \(b^0,b^1\) 的第 \(a_1-a_2+\cdots+(-1)^i\max(a^0_{i+1},a^1_{i+1})\) 位一定不同,得证。
又因为 \(|A|=|B|=2^n\),所以 \(f:A\to B\) 为双射。故答案为 \(E(\sum a_i) = \frac{n(n+1)}{4}\)。
C4
设连通块个数为 \(c\),则 \(c\ge 1+\frac{n(n+1)}{2} - \frac{n(n-1)}{2} = n+1\)。考虑构造一种方案。不妨假设所有直线都不与 \(y\) 轴平行。那么我们把每条直线靠上的一侧涂红。对于每条直线,把涂红的一侧的所有区域的高度都 \(+1\)。可以观察到,所有区域的高度都位于 \([0,n]\) 中,且高度相同的所有区域被连通了,因此构造是正确的。
C5
设 \(n=1009\),则图中有 \(n\) 个度数为 \(n+1\) 的点和 \(n+1\) 个度数为 \(n\) 的点。
首先,图是连通的,因为对于任意两点 \(u,v\),\(\text{deg}(u)+\text{deg}(v)\ge 2n\),故 \(\text{dis}(u,v)\le 2\)。
使用这题的操作,对于不是完全图、不是一个环的任意连通图,都是有解的。下面我们尝试证明这一点。
首先,把图变成一棵树。只需不断进行不改变图的连通性的操作,使边数不断减少。
观察到,对于一个环 \(a_1 - a_2 - \cdots - a_k - a_1\) 和结点 \(u\),如果边 \((u,a_1)\) 存在且边 \((u,a_k)\) 不存在,就可以操作一次使 \((a_1,a_k)\) 不存在、\((u,a_1)\) 不存在、\((u,a_k)\) 存在。这样不改变图的连通性。
考虑图中的最小环,设它的长度为 \(c\)。那么 \(c\ne n\),分类讨论:
- 若 \(c>3\),找到一个不在环上的点 \(u\) 使得它和环上的至少 \(1\) 个点相邻。\(u\) 不可能与环上相邻两点都有边 (否则 \(c=3\)),因此可以选择任意一个在环上且与 \(u\) 相邻的点作为 \(a_k\)。
- 若 \(c=3\),找到图中任意一个点数 \(\ge 3\) 的极大团,找到一个不在团上的点 \(u\) 使得它和团上的至少 \(1\) 个点相邻。由于是极大团,\(u\) 不和团上的所有点相邻,因此可以选择任意一个在团上且与 \(u\) 相邻的点作为 \(a_k\)。
现在图已经变成了树。那么,对于每个点数 \(\ge 3\) 的连通块,必定存在度数 \(\ge 2\) 的点,因此一定能不断进行操作直到满足题意。
C6
不妨假设任意两点的横、纵坐标均不同。把点按照横坐标排序,然后 \(\forall 1\le i\le n\),选择性地交换 \(A_{2i-1}, A_{2i}\) 使得交换后 \(y(A_{2i-1})<y(A_{2i})\)。可以证明这种顺序是合法的。
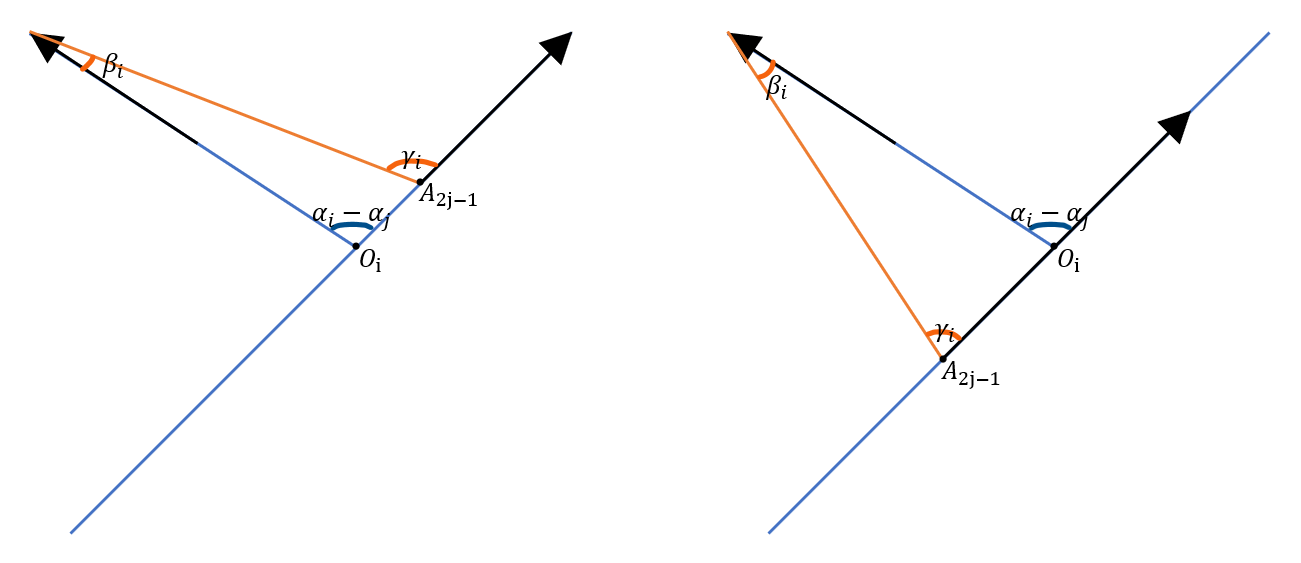
记 \(\vec{v_i}\) 为起点为 \(A_{2i-1}\)、终点为 \(A_{2i}\) 的向量,\(\vec{x^+}\) 为 \(x\) 轴正半轴,\(\alpha_i\) 为 \(\vec{v_i}\) 与 \(\vec{x^+}\) 的夹角。考虑相邻的 \(2\) 个向量 \(\vec{v_i}\) 和 \(\vec{v_j}\) (需要满足 \(j=i\bmod n+1\)),记 \(\beta_i\) 为 \(\angle A_{2i-1}A_{2i}A_{2i+1}\),\(\gamma_i\) 为 \(\angle{A_{2i}A_{2i+1}A_{2i+2}}\)。如果用 \(\pm \beta_i\pm \gamma_i\) 能凑出 \(\alpha_j-\alpha_i\),最终就能凑出 \(\sum \alpha_j-\alpha_i = 0\)。
当 \(\alpha_j = \alpha_i\) 时,\(\beta_i = \gamma_i\),一定正确。对于其它情况,不妨设 \(A_{2i}\) 在 \(A_{2j}\) 的左边,且 \(\alpha_i>\alpha_j\)。记射线 \(A_{2i}A_{2i-1}\) 与直线 \(A_{2j-1}A_{2j}\) 的交点为 \(O_i\),讨论 \(O_i\) 是否在射线 \(A_{2j-1}A_{2j}\) 上,如图,均合法。
C7
设有 \(2m\) 个盒子,第 \(i\) 个盒子里有 \(x_i\) 个球。
首先,\(n=m(m+2)\) 时 Alice 必胜。一开始 Alice 令 \(x_i = |i-m|+1\)。设 \(c_i\) 为当前给 \(x_{1..i}\) \(-1\) 并给 \(x_{i+1..n}\) \(+1\) 的次数 (可以是负数)。无论 Bob 怎么选,Alice 可以将 \(c_{1..m-1}\) 保持在 \([0,1]\) 中,将 \(c_{m..2m-1}\) 保持在 \([-1,0]\) 中,这样永远保证 \(x_i>0\)。
其次,\(n<m(m+2)\) 时 Alice 必败。假设存在 \(x\) 的一个子序列 \(y_k,\cdots,y_1,z_1,\cdots,z_l\) 满足 \(y_k\le k,z_l\le l\)。那么 Bob 的策略如下:
- 指定 \(y_1|z_1\),不妨设 Alice 给前缀 \(-1\)。维护一个操作栈,在栈中加入这个操作。
- 设栈大小为 \(s\),指定 \(y_{s+1}|y_s\)。
- 若 Alice 给前缀 \(+1\),则这次操作和栈顶操作加起来只会让 \(y_s\) \(-1\),那么直接弹栈。
- 若 Alice 给前缀 \(-1\),则将操作加入栈。
- 由于每次弹栈,所有数的总和会变小,因此不可能永远弹栈。最终我们会得到大小为 \(k\) 的栈,使得 \(y_k=0\)。
若 Alice 必胜,\(x\) 不存在该子序列,因此所有区间 \([i-x_i,i+x_i]\) 有交。区间均包含 \(m\) 时 \(n_{\min}=m(m+2)\)。
C8
首先设一个点 \(rt\),初始为 \(1\)。对于 \(i=2..n\) 依次询问 \((rt,i)\),如果是 \(rt\to i\) 则把 \(rt\) 更新为 \(i\)。最后可以得到一棵根为 \(rt\) 的有根内向树,且存在一条主链,所有点都和它的距离不超过 \(1\)。
然后依次询问 \(rt\) 和所有点 \(u\)。如果是 \(u\to rt\),\(u\) 已经有 \(2\) 条出边,直接删掉。直到找到 \(rt\to u,v\) 为止,此时可以删掉 \(rt\)。假设剩余 \(m\) 个点 (\(m\ge 3\)),此时用了 \(2n-m\) 步,且剩余 \(m\) 个点之间问过的边形成森林。每次问 \(2\) 个叶子,可以删掉一个。最终至多剩下 \(2\) 个点,它们之间有边,把它们暴力地和剩余的点问即可。由于 \(m\ge 3\),剩余 \(2\) 点中其中至少 \(1\) 个点和外界有至少 \(1\) 条边已经问过了,总步数 \(2n-2+2n-5 = 4n-7\)。
C9
设 \(f(a_{1..n})\) 为,是否存在 \(x_1<\cdots<x_n\) 使得
当 \(n=1\) 时,\(f(a_1)=1\Leftrightarrow a_1\ge 0\)。
当 \(n\ge 2\) 时,不妨设 \(x_1=0\)。设 \(d\) 满足 \(2^d\le x_n< 2^{d+1}\)。那么 \(\forall 1\le i\le n\),
设
相当于去掉权值为 \(d\) 的边后,\(\forall i\in [1,k]\cup[l+1,n]\),\(s_i\le a_i-1\)。
那么,若 \(f(a_{1..n})=1\),则 \(\exists 1\le k\le l\le n-1\),
对于 \(f(a_{1..n})=1\) 的状态,设 \(\phi(a_{1..n})=\sum_{i=1}^{n} 2^{-a_i}\),那么
- \(n=1\) 时,\(\phi(a_1)\le 1\)
- \(n\ge 2\) 时,\(\phi(a_{1..n})=\) 其后继 \(2\) 个状态的 \(\phi\) 的平均数。
归纳,可以证明 \(\phi(a_{1..n})\le 1\)。因此,符合题意的 \(n_{\max}=2^k\),一种合法方案是 \([0,2^k)\cap \Z\)。


