数轴上连 n 条弦,共有 k 个交点的方案数(原文)
转化问题
首先我们考虑 DP。考虑生成函数,我们用 \(z\) 累计交点数。记 \(F_{i,j}\) 为考虑了前 \(i\) 个点,往后连了 \(j\) 条弦的生成函数。那么一条弦在 DP 中经历 \(2\) 个过程:“产生”和“闭合”,我们在闭合时累加交点数。假设往后连的 \(j\) 条弦中,我们选择从左往右第 \(a\) 条弦在 \(i+1\) 处闭合,那么会有 \(z^{j-a}\) 的贡献。因此,闭合的总贡献就是 \(1+z+\cdots+z^{j-1} = (1-z^j)/(1-z)\)。无论 DP 的路径如何,\((1-z)^{-1}\) 总是会乘恰好 \(n\) 次,所以可以留到最后再乘。我们可以写出 DP 的转移式:
答案为 \((1-z)^{-n}F_{2n,0}\)。
考虑把 DP 状态看作点,转移的路径看作折线,那么相当于枚举所有折线,对于一条折线,设所有\单位线段的“高度”为 \(h_1,h_2,\cdots,h_n\),那么它对答案有 \(\prod (1-z^{h_i})\) 的贡献。
考虑把折线与有根树的 DFS 过程一一对应:/单位线段看作入栈操作,\单位线段看作出栈操作。那么,树的每个非根结点都可能为“普通点”或“关键点”,对于一棵有 \(r\) 个关键点,关键点深度和为 \(k\) 的树,它对答案的贡献为 \((-1)^rz^k\)。
通过构造对合来抵消系数
对于一棵树,我们只保留所有关键点到根的路径的并(虚树),假设还剩下 \(l\) 条边。对于剩下 \(l\) 条边的虚树,考虑把它补全的方案数。相当于在原本的入栈-出栈序列中的 \(2l+1\) 个空隙中分别插入合法括号序列,把长度补到 \(2n\) 的方案数。又相当于长度为 \(2n+2l\) 的括号序列,满足最后 \(2l\) 个位置均为')'的方案数(考虑后 \(2l\) 个位置的匹配位置,将序列分成 \(2l+1\) 段)。可以使用反射法,方案数为 \(\binom{2n}{n+l} - \binom{2n}{n+l+1}\)。
考虑两棵虚树,它们的关键点个数、关键点深度和、边数分别为 \((r,k,l)\) 和 \((r+1,k,l)\),那么它们的贡献会抵消。
让我们重新列举一下合法虚树需要满足的条件:
- 结点无标号,但可能为“关键点”;
- 所有叶子必为“关键点”;
- 所有“关键点”的深度之和为 \(n\) \((n\ge 1)\);
- 结点的儿子之间有先后顺序。

因为所有叶子都是关键点,所以在 DFS 的过程中,如果出现入栈之后立即出栈的情况,则一定访问到了关键点。
我们可以按 DFS 中的出栈顺序给“关键点”标上 \(1..k\) 的编号。
设在“关键点” \(i\) 出栈前,入栈、出栈操作分别进行了 \(a_i,b_i\) 次。可以观察到下列性质:
- \(\sum_{i=1}^{k} b_i-a_i = n\);
- \(1\le a_1\le a_2\le \cdots\le a_k\);
- \(0= b_1 < b_2 < \cdots < b_k\);
- \(b_i<a_i\) \((\forall 1\le i\le k)\);
- \(b_{i+1}\le a_{i}\) \((\forall 1\le i \le k)\);
- 树的边数是 \(a_k\);
- 合法的序列 \((a_1,b_1), (a_2,b_2), \cdots, (a_k,b_k)\) 与合法的树构成双射。
为了方便表示,我们把合法序列画成方格图:假设有一个向右、向上无限延伸的方格图,我们只保留最下面的 \(k\) 行,对于从下往上的第 \(i\) 行,我们只保留第 \(b_i+1\) 到第 \(a_i+1\) 个格子。这样,画出的方格图是联通的。
为了体现 \(b_k<a_k\) 这条性质,我们在方格图第 \(k\) 行第 \(a_k+1\) 个格子上方添加一个格子。
考虑按照下图中的方法构造对合:
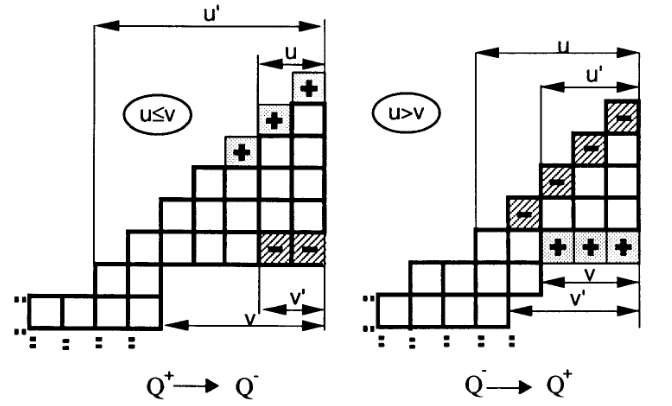
这样,在大部分情况中,我们总能把合法的方格图完美匹配,每对匹配的宽度相同、高度差 \(1\),这使得它们在答案的式子中抵消了。所有不能被匹配的方格图都属于下面这种情况:
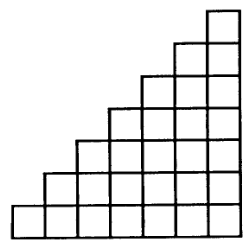
因此,原答案和只保留这种情况的答案是一样的。答案为:
也可以写成:


