数轴上连 n 条弦,共有 k 个交点的方案数
问题
数轴上有 \(2n\) 个点,考虑所有用 \(n\) 条弦将它们完美匹配的方案,有多少种方案会产生 \(k\) 个交点(不考虑三线共点)?
在 OEIS 上为A067311。
分析
本文主要是对这篇论文的翻译。
令 \(dp_{i,j,k}\) 表示:考虑了前 \(i\) 个点,其中的 \(j\) 个点要往后 \(n-i\) 个点连边,当前共产生了 \(k\) 个交点的方案数。
考虑对于任意 \(a<b<c<d\),在 \(c\) 处统计 \((a,c)\) 和 \((b,d)\) 的交点。若第 \(i+1\) 个点往前连,产生 \(k_0\) 个交点的方案数为 \([k_0< j]\)。我们把 \(dp_{i,j}\) 看作生成函数,那么:
答案为 \(dp_{2n,0}\)。可以发现 \((1-z)^{-1}\) 总是会乘 \(n\) 次,因此可以放到最后再乘。直接做的时间复杂度是 \(O(n^4)\)。
根据这个 DP,可以把原问题转化为以下问题:
- 枚举所有长度为 \(2n\),只包含 \(\pm 1\),和为 \(0\) 且任意前缀和 \(\ge 0\) 的序列 \(c_{1..2n}\);
- 设 \(s_i\) 为 \(a_{1..i}\) 的总和,则 \(c\) 对答案有 \(\prod_{c_i=-1} (1-z^{s_{i-1}})\) 的贡献。
我们把 \(\pm 1\) 分别看作 DFS 过程中的入栈、出栈,那么一个合法序列对应一棵儿子有顺序的有根树。
对于每个出栈操作,如果它的贡献是 \(-z^{s_i-1}\) 则将弹出的点标记为关键点,否则标记为普通点。我们只关注所有关键点到根的路径的并,也就是虚树。
假设虚树中有 \(l\) 条边,考虑计算可能的原树的个数(设为 \(t_{n,l}\)):
- 观察到,能插入一棵树的位置个数恰好为 \(2l+1\)。
- 相当于合法括号序列生成函数的 \(2l+1\) 次方的 \(n-l\) 次项系数。
- 这等价于,长度为 \(2n+2l\),后 \(2l\) 个位置均为
)的合法括号序列个数。 - 即从 \((0,0)\) 走到 \((n-l,n+l)\),每次只能往右或往上走 \(1\) 单位长度,途中不经过 \(y<x\) 的点的方案数。
- 使用反射法,得到方案数为:
现在,我们考虑所有关键点深度和为 \(d\) 的虚树。不妨来观察 $d=2 $ 的情形:两种虚树均有 \(l=2\),关键点个数相差 \(1\),它们对答案的贡献抵消了。因此,我们的目标是:找到包含大部分虚树的匹配,每对匹配中的两棵虚树的 \(l\) 相同且关键点个数相差 \(1\)。
我们按照出栈顺序(也就是原序列中的顺序)考虑所有关键点。假设第 \(i\) 个关键点对应原序列中的 \(c_j\),设 \(a_i,b_i\) 分别为 \(c_{1..j-1}\) 中 \(+1,-1\) 的个数。
考虑将虚树对应到一种方格表。我们用 \((i,j)\) 表示从下往上第 \(i\) 行,从左往右第 \(j\) 列的方格。在方格表中,我们只保留所有 \((i,b_i..a_i)\) 的方格。假设有 \(k\) 个关键点,我们额外保留 \((k+1,a_k)\) 这个方格。

可以观察到,合法的 \((a_1,b_1),(a_2,b_2),\cdots,(a_k,b_k)\) 序列和满足如下条件的方格表一一对应:
- 方格表连通。
- 每行都是一个区间,从下往上考虑,则区间的右端点不降,左端点递增。
- 最上面一行只有 \(1\) 个方格。
现在设方格表右上角为 \((0,0)\)。设 \(u\) 为最大的 \(u_0\),使得 \(\forall 0\le i<u_0, (-i,-i)\) 均为本行第一个格子。设 \(v\) 为最大的 \(v_0\),使得 \(\forall 0\le i<v_0\),第 \(-i\) 列最下面的格子与第 \(0\) 列最下面的格子位于同一行。
我们可以按照如下方式构造:
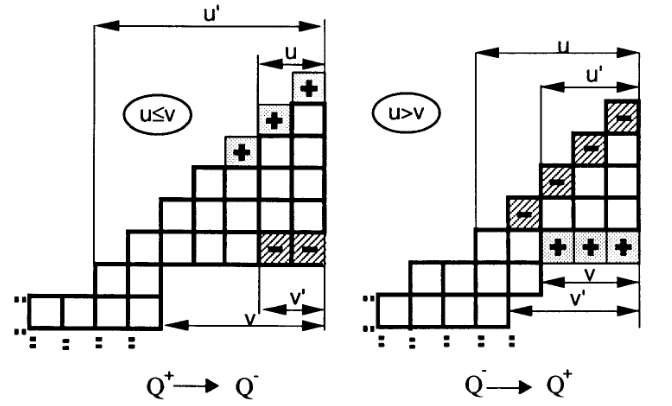
最终,未匹配的方格表一定是如下形式:共有 \(l+1\) 行,从上往下第 \(i\) 行有 \(i\) 个方格。因此,答案的生成函数为:


