Two-Processor Scheduling
Two-Processor Scheduling 问题:给定 DAG,每次可以选至多 2 个入度为 0 的点同时删除,问最少几次删完。
记 \(u\prec v\) 表示 \(u\) 在 DAG 上能走一条路径到达 \(v\),读作 “\(u\) 到达 \(v\)”。记 \(u\to v\) 表示 \(u\prec v\) 且不存在 \(w\) 使 \(u\prec w\prec v\)。如果我们构建一张无向图,两点之间连边当且仅当 \(u\not\prec v\) 且 \(v\not \prec u\),那么 (这张无向图的最大匹配) + (原 DAG 上的最少删除次数) = \(n\)。大概可以通过调整法来构造原问题的一组解。然而这和下面的内容没啥关系。
下面将叙述论文中的做法。在构造方案前,先给每个点一个标号 \(\alpha[u]\),满足 \(\alpha\) 为一个排列。我们按照 \(i=1..n\) 的顺序依次确定 \(\alpha[u]=i\) 的点。设 \(N[u]\) 表示集合 \(\{\alpha[v]|u\to v\}\) 从大到小排序的序列。每次,我们选择出度为 0 的点中 \(N[u]\) 字典序最小的点,将 \(\alpha[u]\) 设置为 \(i\),然后对于所有 \(v\to u\) 令 \(v\) 的出度减 \(1\)。构造方案时,每次选择入度为 0 的点中 \(\alpha[u]\) 最大的至多 2 个点删掉。
考虑加速标号的过程。可以看成尚未标号的点形成一个序列,每次标一个点 \(u\) 时将所有 \(v\to u\) 的点删掉,按照原顺序依次放到序列末尾。每次选择出度为 0 的点中在序列中最靠前的。维护每个点在序列中的下标(删点时不改变其余点的下标),既可使用带修改的堆队列维护每次位置最小的点。
下面叙述算法的正确性。假设有两个序列 \(S,T\),每次操作会删掉 1 或 2 个点,优先将 \(\alpha[u]\) 大的点放入 \(S\),将剩下的点(若不存在则认定为特殊点 \(\varnothing\),定义 \(\alpha[\varnothing]=0\))放入 \(T\)。有以下事实:
- 若 \(u\prec v\),则 \(\alpha[u]>\alpha[v]\)。
- \(\alpha[S[i]]>\alpha[T[i]]\)。
- \(\alpha[S[i]]>\alpha[S[i+1]]\)。
第 3 条可以考虑反证,假设 \(S[i+1]\) 不能和 \(S[i]\) 换,那么它肯定能被 \(S[i]\) 或者 \(T[i]\) 到达,这样就推出 \(\alpha[S[i]]>\alpha[S[i+1]]\),从而导出矛盾。
设 \(S,T\) 中最后一个元素分别为 \(p_1,q_1\)。设 \(q_{i+1}\) 为 \(T\) 中从 \(q_i\) 的前一位开始,往前找到第一个满足 \(\alpha[u]<\alpha[p_{i}]\) 的点,\(p_{i+1}\) 为与 \(q_{i+1}\) 在同一轮删除的点。
假设一共找到了 \((p_1,q_1),\cdots,(p_k,q_k)\)。如果 \(k=1\),那么 \(T\) 中 \(\varnothing\) 只可能出现在末尾,直接得证。否则我们考虑将点分组,例如下面的绿色区域从右到左分别是第 \(1,2\) 组(蓝色点不分进任何组)。
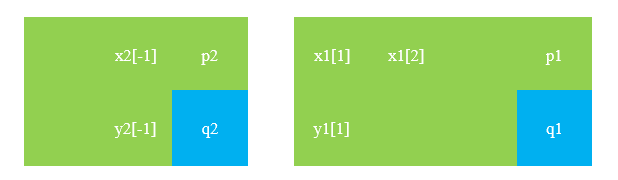
我们先只考虑从右到左的第 \(1,2\) 组。根据之前分析的性质以及分组过程,有:
设 \(X_1[1]\) 为 \(u\),考虑 \(u\) 为什么不能和 \(q_2\) 换。这一定是因为 \(p_2\prec u\) 或者 \(q_2\prec u\),然而 \(\alpha[q_2]<\alpha[u]\),所以只可能 \(p_2\prec u\)。然后我们依次考虑 \(Y_1[1],X_1[2],Y_1[2],\ldots,Y_1[-1],p_1\),它们要么是被 \(p_2\) 到达,要么是被第 \(1\) 组的之前的点到达,归纳得到第 \(1\) 组内的点全都被 \(p_2\) 到达。
再设 \(Y_2[-1]\) 为 \(v\),那么 \(\alpha[v]>\alpha[p_2]\),考虑为什么 \(N[v]\ge N[p_2]\)。这一定是因为 \(v\) 要么到达整个第 \(1\) 组,要么到达 \(p_2\) 从而到达整个第 \(1\) 组。然后我们依次考虑 \(X_2[-1],Y_2[-2],X_2[-2],\ldots,X_2[1]\),它们要么到达第 \(1\) 组,要么到达第 \(2\) 组中后面的点,归纳得到第 \(2\) 组中所有点到达第 \(1\) 组中所有点。
我们能类似地证明第 \(i+1\) 组所有点到达第 \(i\) 组所有点。由于每组内不出现 \(\varnothing\),即使去掉蓝色点也至少需要当前方案的操作次数,因此得证。

